7 Analiza preživetja
7.1 Analiza preživetja – Kaplan-Meierjeva krivulja
Uvozimo datoteko HeartValveSurvival.xls v SPSS z ukazom File -> Import Data -> Excel… in naložimo podatke iz lista SurvivalData SPSS.
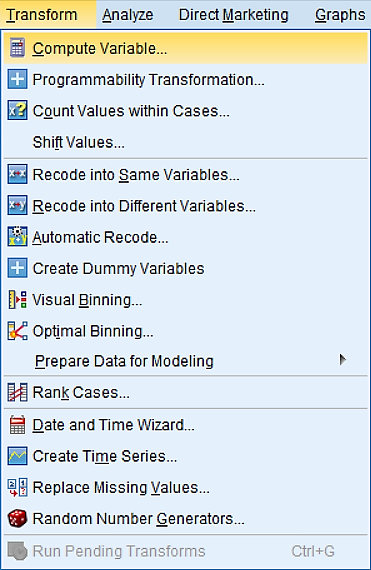
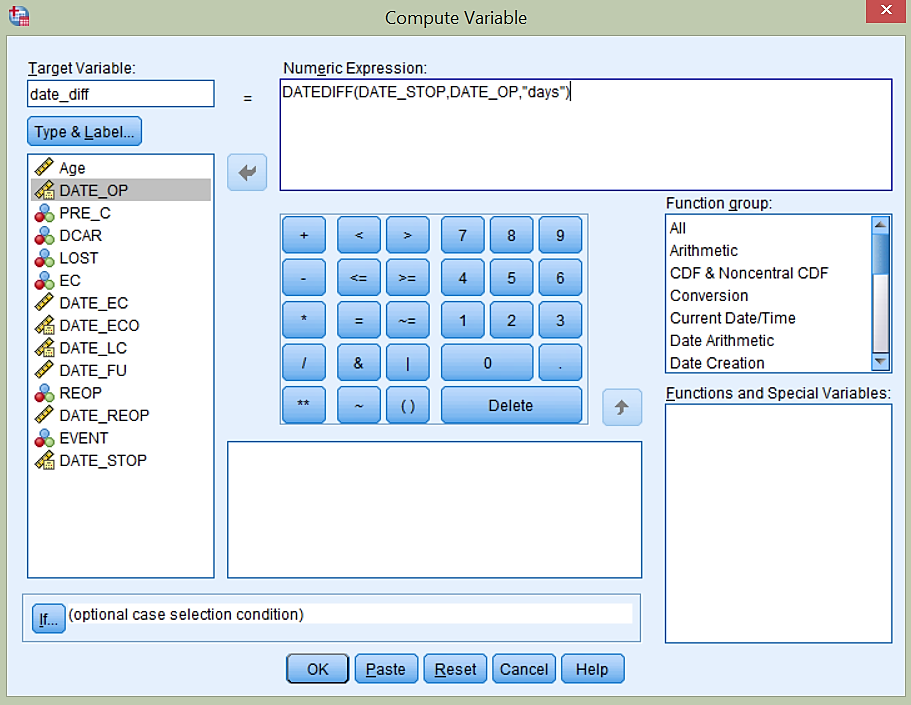
Da lahko določimo tabelo preživetja pacientov po operaciji srca moramo izračunati, koliko dni po operaciji smo pridobili dogodke. To naredimo tako, da izračunamo razliko med datumi dogodkov in datumi od operacije. Tako ustvarimo novo spremenljivko, ki nam bo povedala število dni po operaciji. To naredimo z ukazom Transform -> Compute Variable…
Novo spremenljivko poimenujemo date_diff. Nato uporabimo logični operator DATEDIFF. V oklepaju najprej navedemo spremenljivko, ki nam pove, kdaj se je zgodil dogodek oziroma je pacient izstopil iz raziskave, nato navedemo spremenljivko, ki nam pove kdaj je bil pacient operiran in nato v navednicah dodamo še, v kakšni enoti želimo imeti izražen čas, kar prikazuje slika spodaj.
V Data View se lahko prepričamo, da imamo novo spremenljivko, ki meri dneve od operacije.
Sedaj bomo določili tabelo preživetja pacientov po operaciji srca z ukazom Analyze -> Survival -> Life Tables…
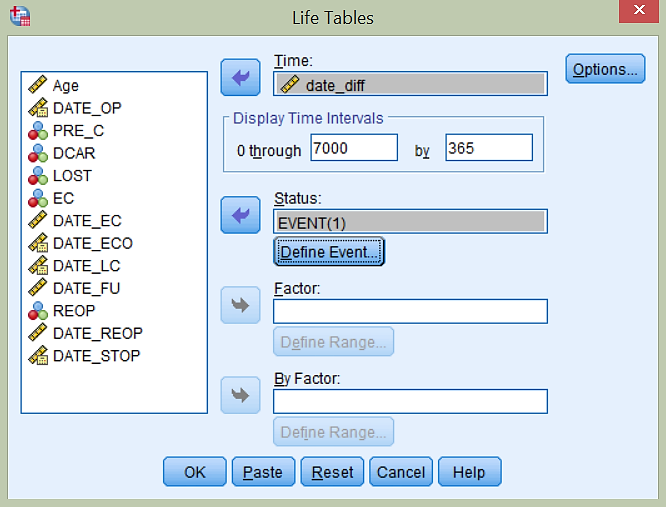
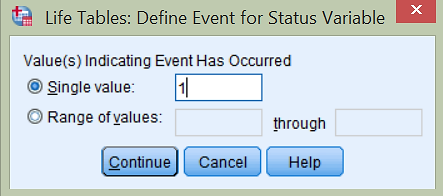
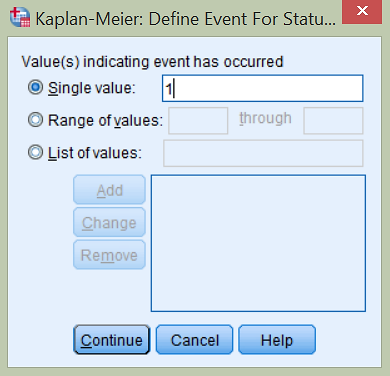
Spremenljivko date_diff prenesemo v Time. Določimo interval, da želimo izpisati tabelo preživetja do 7000 dni in sicer po intervalih na 365 dni. Določimo še Status, v katerega prenesemo spremenljivko EVENT, s katero določimo (klik na gumb Define Event…), da 1 pomeni, da se je dogodek zgodil (Value(s) Indicating Event Has Occured).
Prikazan je izsek tabele preživetja, ki jo izpiše SPSS.
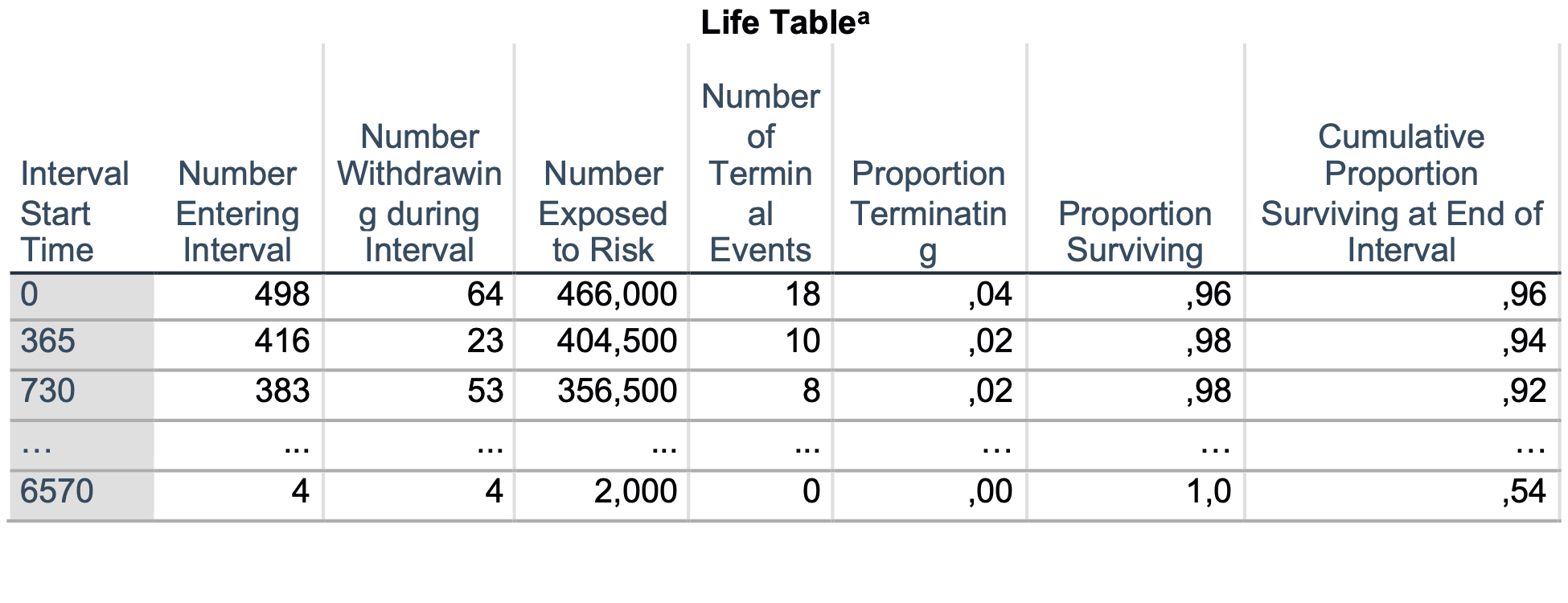
Interval Start Time pove časovni interval. Number Entering Interval pove, koliko ljudi je vstopilo v analizo v tem intervalu. Number Withdrawing during Interval pove, koliko oseb je v tem času zapustilo analizo (cenzurirani podatki). Number Exposed to Risk so vse osebe, ki so vstopile v analizo v tem intervalu, od katerih odštejemo polovico oseb, ki so zapustili analizo. Number of Terminal Events pa pove, koliko dogodkov se je zgodilo v nekem intervalu. Proportion Terminating izračuna delež dogodka v tem intervalu. Delež, da se dogodek ni zgodil je predstavljen v stolpcu Proportion Surviving. Cumulative Proportion Surviving at End of interval pove, kakšna je verjetnost preživetja po določenem času.
Tako lahko ugotovimo, da je po prvem letu (365 dni) skupna verjetnost, da se dogodek (smrt, endokarditis, ponovna operacija) ne bo zgodil (verjetnost preživetja), 96 %, v drugem 94 %, po 6570 dneh obstaja 54 % verjetnost preživetja.
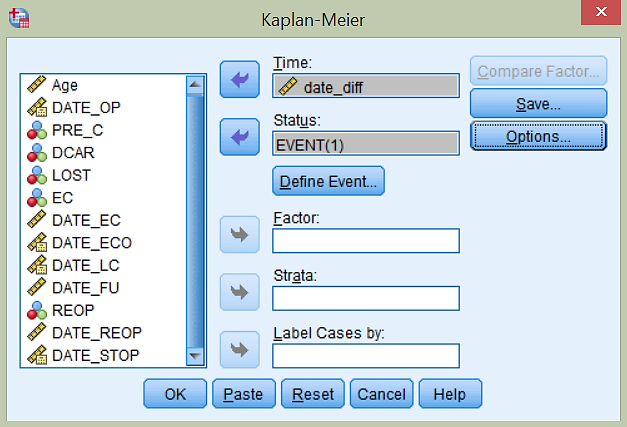
Sedaj narišimo še Kaplan-Meierjevo krivuljo. Uporabimo ukaz Analyze -> Survival -> Kaplan-Meier…
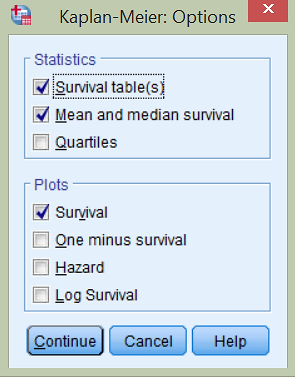
Za čas ponovno izberemo spremenljivko date_diff. Določimo Status, v katerega prenesemo spremenljivko EVENT, s katero z 1 določimo, da se je dogodek zgodil (klik na gumb Define Event…). S klikom na gumb Options… odkljukamo še Survival. Opazimo, da nismo določili časovnega intervala, kakor pri analizi preživetja, saj so pri Kaplan-Meierjevi krivulji preživetja intervali definirani od enega do drugega dogodka v podatkih.
V izvedbenem oknu se nam izpiše tabela preživetja, vendar sedaj za vsak dogodek posebej. Hkrati se izriše Kaplan-Meierjeva krivulja preživetja.
Iz grafa razberemo, da so na x-osi navedeni podatki o času v dnevih, na y-osi pa verjetnost preživetja do trenutnega časa. S križci so označeni cenzurirani podatki. Krivulja preživetja je vedno padajoča funkcija. V našem grafu lahko prebiramo verjetnosti preživetja do izbranega časa. Tako lahko npr. ugotovimo, da je po 2000 dnevih verjetnost preživetja približno 85 %, po 4000 dnevih je verjetnost preživetja 65 %, po 6000 dnevih pa je verjetnost preživetja 54 %.
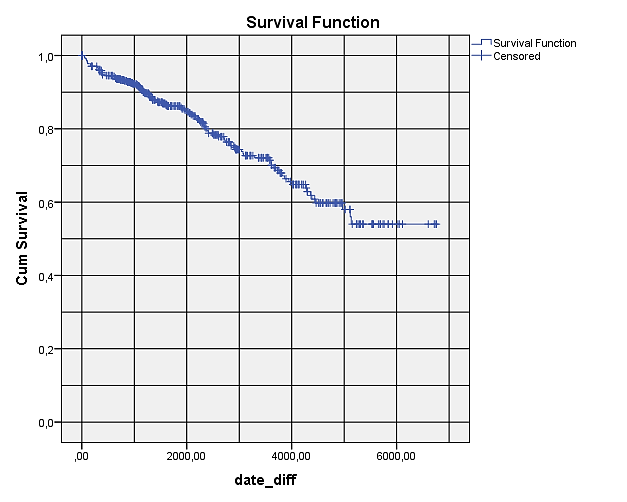
Za lažje branje grafa smo dodali mrežne črte. Dvokliknemo na graf. Izberemo ikono Show Grid Lines. V zavihku Grid Lines izberemo Both major and minor ticks.
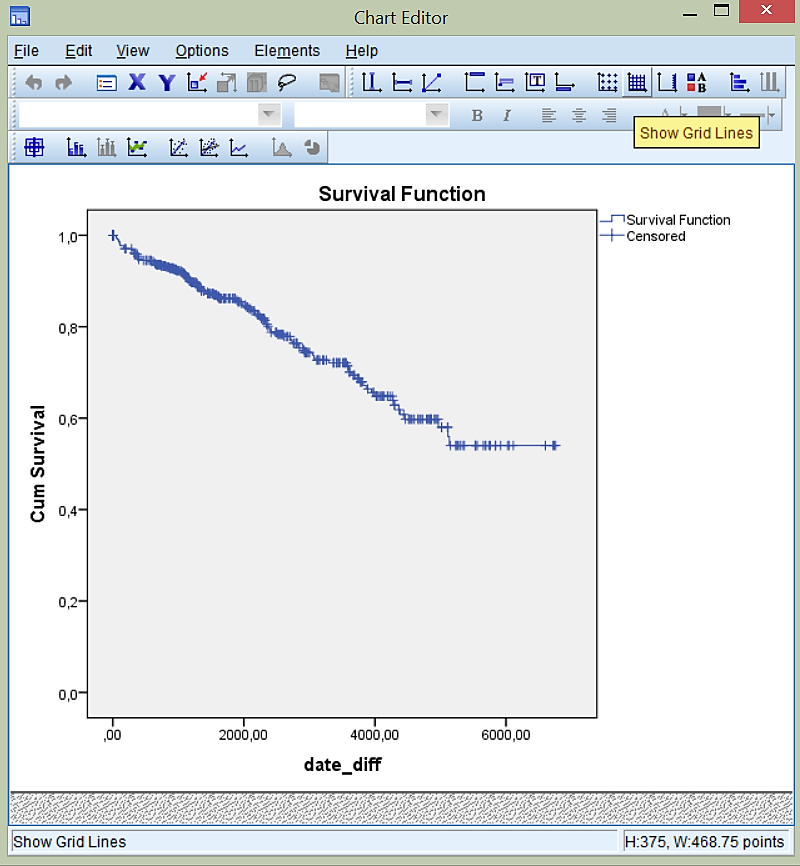
Poleg grafa se nam izpiše tudi naslednja tabela:
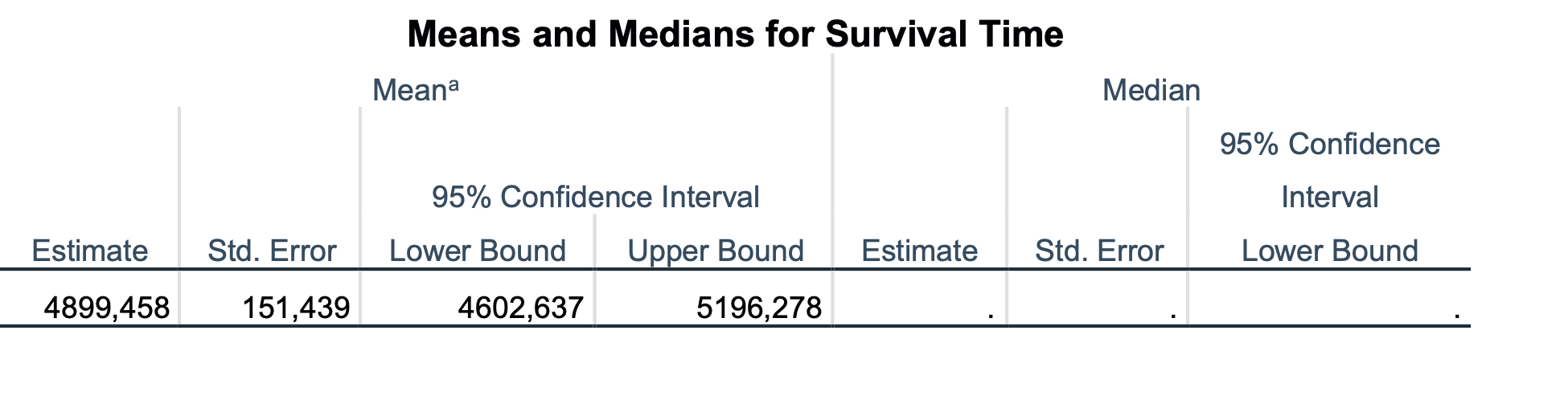
V tabeli je izračunan povprečni čas preživetja, to je čas, pri katerem se preživetje zmanjša na polovico. V našem primeru je do konca časa preživetje 54 %, torej nikoli ne pade na 50 %. Kljub temu je ocenjen povprečni čas preživetja 4899.5 dni. Običajno se podaja medianin čas, ki ga pa v našem primeru ne moremo izračunati, saj je preživetje na koncu naše analize višje od 50 %.
Krivulje preživetja lahko med sabo tudi primerjamo, npr. če primerjamo dve skupini pacientov, ki so bili zdravljeni po dveh metodah, ali pa v našem primeru glede na to, ali so pacienti imeli resne težave ali manjše težave pred operacijo glede na lestvico NYHA.
Recimo, da so resne težave po lestvici NYHA pri 3. in 4. stopnji, pri stopnjah NYHA < 3 pa manj resne težave. Tako bomo paciente v našem primeru ločili na dve skupini pacientov glede na spremenljivko PRE_C. Če je PRE_C > 2, je skupina z resnimi težavami, sicer pa z manj resnimi težavami. Zato bomo ustvarili bomo novo spremenljivko, ki bo imela vrednost 1 v primeru PRE_C > 2 in 0 sicer.
Novo spremenljivko nyha_01 ustvarimo z ukazom Data -> Compute Variable…
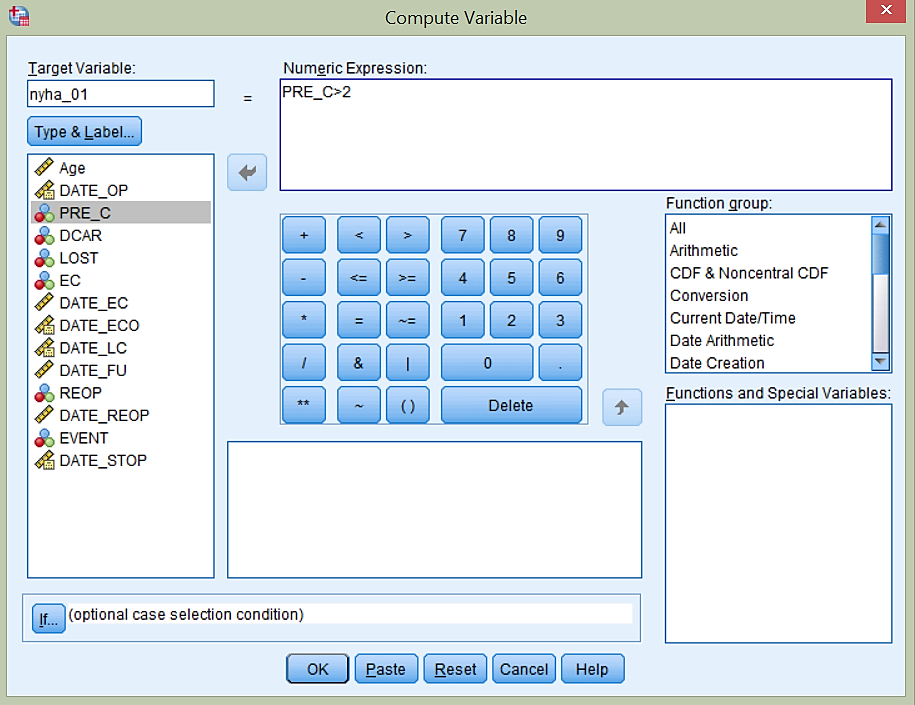
V zavihku Data View se pojavi nova spremenljivka nyha_01, kot prikazuje spodnja slika.
Da bi primerjali krivulji preživetja pri obeh skupinah glede na nyha_01 izvedemo Kaplan-Meierjevo analizo preživetja. To naredimo z ukazom Analyze -> Survival -> Kaplan-Meier…
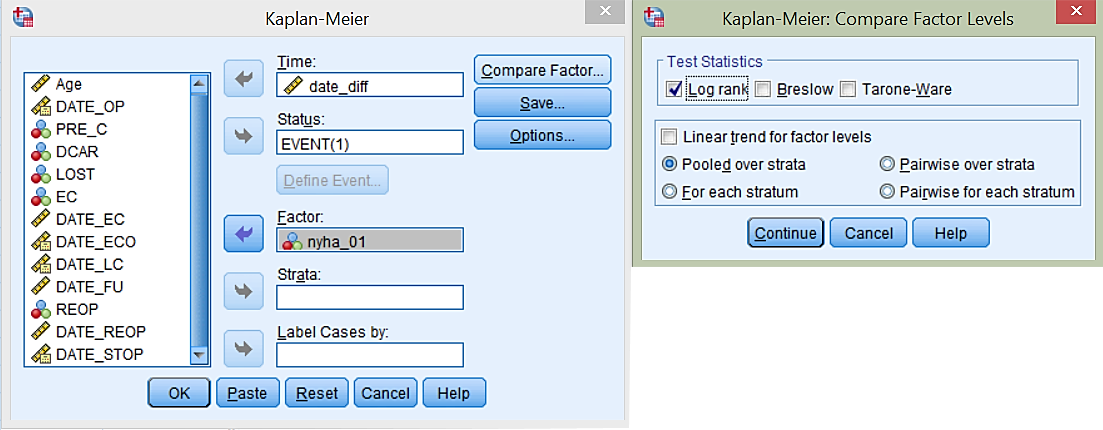
Vse pustimo tako kot je bilo v primeru izrisa prejšnje krivulje preživetja. Dodamo pa še spremenljivko nyha_01 kot faktor. Za primerjavo med krivuljama preživetja še izberemo statistični test s klikom na gumb Compare Factor…, kjer označimo Log rank za testno statistiko.
V izvedbenem oknu SPSS se izrišta dve Kaplan-Meierjevi krivulji preživetja, ki sta prikazani spodaj.
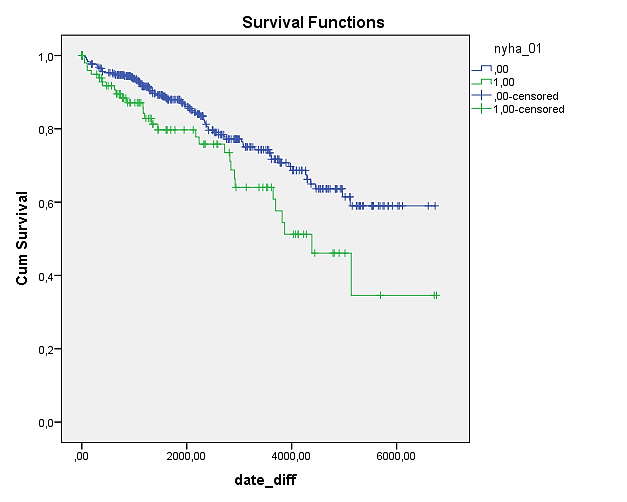
Zelena krivulja predstavlja Kaplan-Meierjevo krivuljo preživetja tistih pacientov, ki so pred operacijo imeli resne težave (nyha_01 = 1), medtem ko modra Kaplan-Meierjeva krivulja preživetja prikazuje paciente, ki pred operacijo niso imeli težav oziroma so bile manjše (nyha_01 = 0). Že iz grafa krivulj preživetja lahko ugotovimo, da se dogodki v primeru pacientov z manjšimi težavami pojavljajo kasneje kot v primeru pacientov z resnimi težavami.
To dodatno potrdimo z izvedbo log-rank statističnega testa z rezultati v spodnji tabeli.
Testna statistika pove, da je razlika med krivuljama preživetja pri pacientih z resnimi težavami pred operacijo in pacientih z manjšimi težavami pred operacijo statistično značilna (p = 0.015).
7.2 Analiza preživetja – Coxov regresijski model
Ponovimo začetne korake (uvoz datoteke in kreiiranje nove spremenljivke date_diff) iz vaje pog. 7.1.
Za izvedbo Coxovega regresijskega modela uporabimo ukaz Analyze -> Survival -> Cox Regression …
S Coxovo regresijo modeliramo razmerje med tveganji za pojav slabega dogodka (v našem primeru smrti, endokarditisa ali ponovne operacije) glede na faktorje tveganja. V našem primeru je faktor tveganja, ki ga preučujemo starost v spremenljivki age. Podatke v oknu Cox Regression izpolnimo, kot je prikazano na sliki:
Časovna spremenljivka je v našem primeru date_diff, statusna spremenljivka EVENT, kjer dogodek definiramo z vrednostjo 1 z gumbom Define Event … Dodatno označimo z gumbom Options… še izpis intervalov zaupanja v ocene regresijskih koeficientov (CI for exp(B)), kot je prikazano spodaj.
Ker bomo izrisali krivulje preživetja ob različnih starostih, pa z gumbom Plots … izberemo ustrezni graf. V našem primeru bomo najprej izrisali krivuljo preživetja za povprečno starost (v našem primeru 47.2 leta), zato pustimo označeno, kot je prikazano:
V izvedbenem oknu SPSS se izvede Coxova regresijska analiza. Zanima nas tabela, ki je prikazana v nadaljevanju:
Iz tabele lahko razberemo, da je regresijski koeficient enak 0.021 in je pozitiven, kar pomeni, da se z višanjem starosti povečuje tveganje za slabe dogodke. Za koliko, pa lahko ugotovimo iz Exp(B), ki je v našem primeru 1.021. To pomeni, da se tveganje za slabe dogodke povečuje za vsako leto starosti za 1.021-krat. Ker interval zaupanja ne vsebuje vrednosti 1.0, je to povečanje statistično značilno, kar je tudi izračunano v tabeli (p = 0.006).
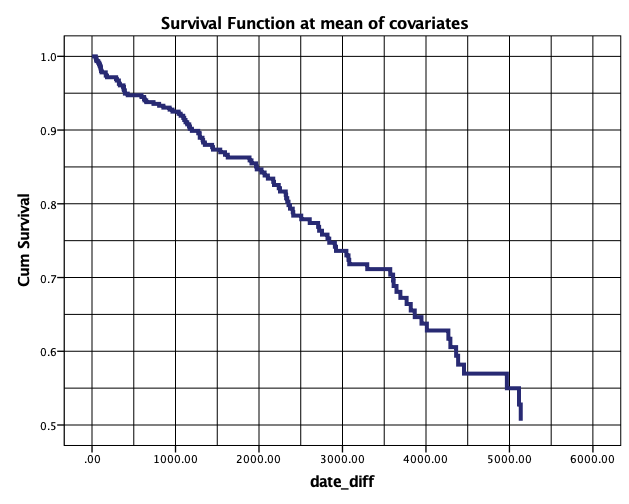
Poleg tabel se izriše tudi graf, ki prikazuje krivuljo preživetja posameznika pri povprečni starosti 47.2 let.
Ker nas zanimajo še krivulje preživetja pacientov pri starosti 20 in 60 let, to lahko narišemo tako, da ponovimo postopek modeliranja s Coxovo regresijo iz prej predstavljenih postopkov in pri grafih z gumbom Plots… izberemo izris krivulje pri vrednosti 20 ali pri vrednosti 60, kot je prikazano v nadaljevanju. Izris grafov moramo izvesti vsakič ločeno.
Pri tem se izrišeta grafa krivulj preživetja pacienta pri 20-ih letih in graf krivulje preživetja pacienta pri 60-ih letih.
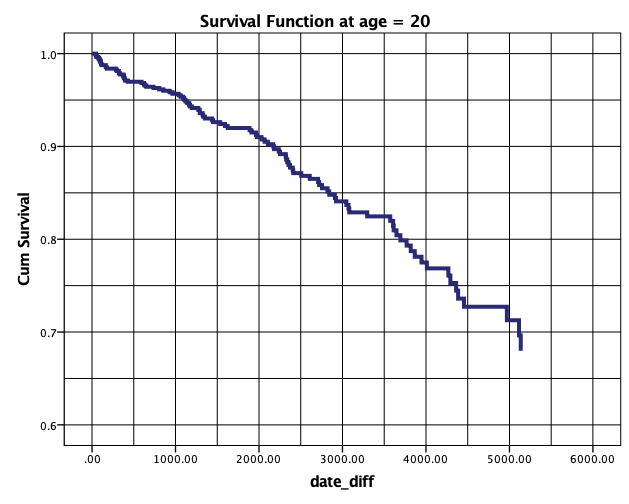
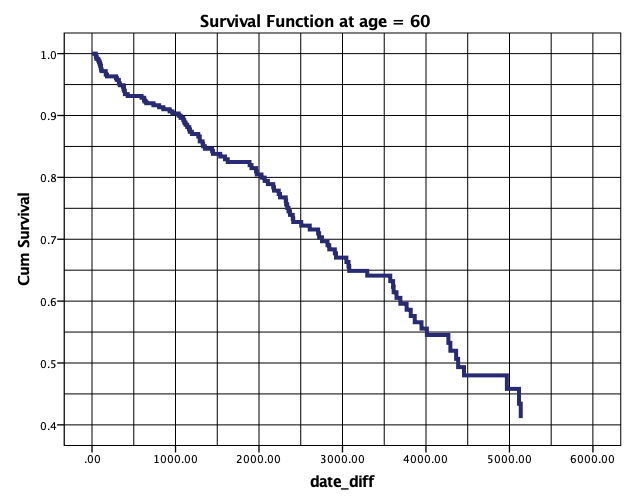
Vse tri grafe krivulj preživetja pacientov pri 20-ih, 60-ih letih in pri povprečni starosti lahko primerjamo med sabo. Ugotovimo lahko, da krivulja preživetja počasneje pada pri pacientu s starostjo 20, potem pri povprečni starosti in najhitreje pri pacientu pri starosti 60. Tako lahko npr. primerjamo krivulje preživetja pri 2000 dnevih: pri 20-letnemu pacientu je verjetnost, da se dogodek ne bo zgodil, nad 0.9, pri povprečno staremu je že 0.85, pri 60-letnemu pacientu pa približno 0.8. Na tak način lahko primerjamo verjetnosti tudi pri drugih časih. Te ugotovitve pa so tudi skladne s Coxovim regresijskim modelom, s katerim smo ugotovili naraščanje tveganja za pojav slabih dogodkov z višanjem starosti.
V Coxov regresijski model bomo sedaj poleg starosti uvrstili tudi skupino pacienta glede na srčne bolečine po NYHA, kot smo jih definirali že pri vaji 7.1. Ko definiramo novo spremenljivko nyha01, jo dodamo v regresijski model s ponovno izvedbo ukaza Analyze -> Survival -> Cox Regression … Coxov regresijski model definiramo enako kot prej, le da poleg spremenljivke age damo kot faktor tveganja v model še spremenljivko nyha01.
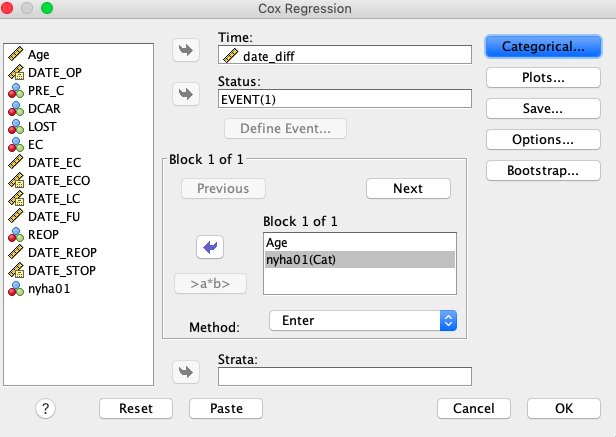
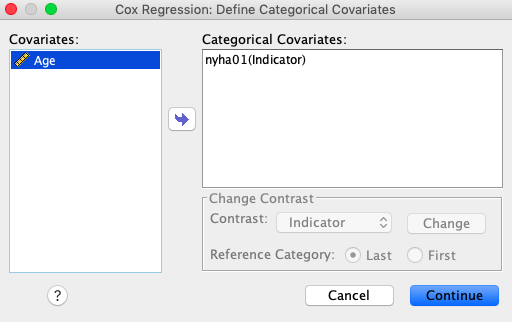
Ker je spremenljivka nyha01 kategorijska, moramo to označiti v modelu. To naredimo z gumbom Categorical…, kjer označimo spremenljivko nyha01 za kategorijsko, obenem pa še določimo, da je zadnja kategorija referenčna (rezultate modela bom interpretirali v primerjavi z zadnjo kategorijo). Dodatno bomo tudi izrisali krivulji preživetja za skupini nyha01 ločeno v primeru povprečno starega pacienta. To naredimo z gumbom Plots…, kjer izberemo graf, kot je prikazano na sliki desno spodaj.
V izvedbenem oknu se nam izpišejo rezultati Coxove regresije. Pomembna je tabela z regresijskimi koeficienti in graf krivulj preživetja glede na obe skupini pacientov.
Iz tabele lahko razberemo, da je razmerje med tveganji (stolpec Exp(B)) pri spremenljivki starost (Age) enako 1.022, kar pomeni, da se za vsako leto starosti tveganje za slab dogodek poveča za 2.2 %. Razmerje med tveganji se je malenkost spremenilo v primerjavi s prejšnjim Coxovim regresijskim modelom. Ker interval zaupanja ne vsebuje 1.0, je povečanje statistično značilno.
Pri spremenljivki nyha01, ki je kategorijska, pa pomeni Exp(B) = 0.581 to, da je tveganje za slab dogodek 0.581-krat manjše v primeru prve skupine (nyha01 = 0) v primerjavi z drugo skupino pacientov (nyha01 = 1), ker smo tako organizirali referenčno kategorijo.
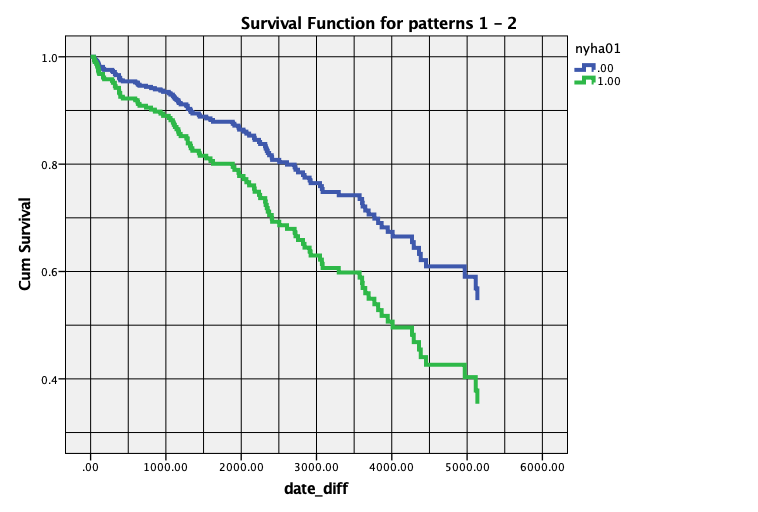
Razmerje med tveganji Exp(B) = 0.581 pri dveh skupinah lahko prevedemo tudi na krivulje preživetja. To pomeni, da je (preživetje prve skupine) = (preživetje druge skupine)\(^{0.581}\). To lahko opazujemo tudi na grafu krivulj preživetja, ki sta izrisani pri povprečni starosti pacienta. Tako lahko izračunamo eno preživetje iz drugega na naslednji način: če npr. poznamo verjetnost preživetja druge skupine pri času 2000 dni, ki je enako 0.79 (iz grafa), lahko izračunamo verjetnost preživetja prve skupine kot \(0.79^{0.581} = 0.872\), kar lahko potrdimo iz grafa. Na enak način lahko računamo tudi pri ostalih časih.