# Začetni model brez spremenljivk
empty_mod <- lm(FTW ~ 1, data=data)
# Statistika modela
summary(empty_mod)
# Končni model z vsemi spremenljivkami
full_mod <- lm(FTW ~ BPD + FL + AP + CP, data=data)
# Statistika modela
summary(full_mod)
# Koračna metoda: forward
# Štartamo z empty_mod in končamo s full_mod
mod = step(empty_mod, direction = "forward", scope=formula(full_mod))
# Statistika modela
summary(mod)6 Regresijska analiza
6.1 Korelacije
Postopek reševanja
V Excel datoteki imamo različne meritve, ki jih dobimo pri impedančni spektroskopiji. V Jamovi odpremo podatke z izbiro Open in odpremo ustrezno Excelovo datoteko Breast Tissue.xlsx.
V prvem stolpcu imamo spremenljivko, ki določa vrsto tkiva, v ostalih stolpcih pa so zbrane meritve pacientov pridobljene z impedančno spektroskopijo: I0, PA500, HFS, DA, AREA… Opazimo, da vrstice 107-110 za našo analizo niso relevantne, zato jih označimo in izbrišemo. Kako izbrišemo vrstice, si lahko ogledate v nalogi pog. 5.1.
Želimo ugotoviti katere spremenljivke so tako imenovani kofaktorji. To so spremenljivke, ki so korelacijsko povezane. Narišemo graf medsebojnih odvisnosti za vse pare meritev: Analyses -> Regression -> Correlation Matrix.
Nato označimo vse skalarne spremenljivke I0, PA500, HFS, DA, AREA, A/DA, MAX IP, DR, P in pod možnostjo Plot izberemo Correlation matrix.
V rezultatskem oknu se nam izriše matrika grafov kombiniranih za vse pare meritev.
Poglejmo na primer, kako je spremenljivka P korelirana z ostalimi spremenljivkami (gledamo zadnjo vrstico matrike).
- Spremenljivki P in I0 sta močno korelirani in sicer linearno, saj lahko na graf položimo premico, ki se približno prilega podatkom.
- Spremenljivki P in PA500 nista korelirani.
- Spremenljivki P in HFS nista korelirani.
- Spremenljivki P in DA sta korelirani, vendar ne nujno linearno.
- Spremenljivki P in AREA sta korelirani in sicer močno navzgor. Pri tej povezavi imamo en izrazit odstopajoči par meritev.
- Spremenljivki P in A/DA sta korelirani.
- Spremenljivki P in MAX IP sta korelirani.
- Spremenljivki P in DR sta korelirani.
Korelacijo potrdimo, ko lahko na graf položimo krivuljo, ki se približno prilega meritvam. Nekaj korelacij opazimo takoj, nekatere pa niso očitne, oziroma jih ni.
Za ugotavljanje povezanosti spremenljivk in sicer linearno povezanih z normalno porazdelitvijo bomo uporabili Pearsonovo korelacijo. Spearmanova korelacija meri nelinearno povezanost spremenljivk, če podatki niso normalno porazdeljeni.
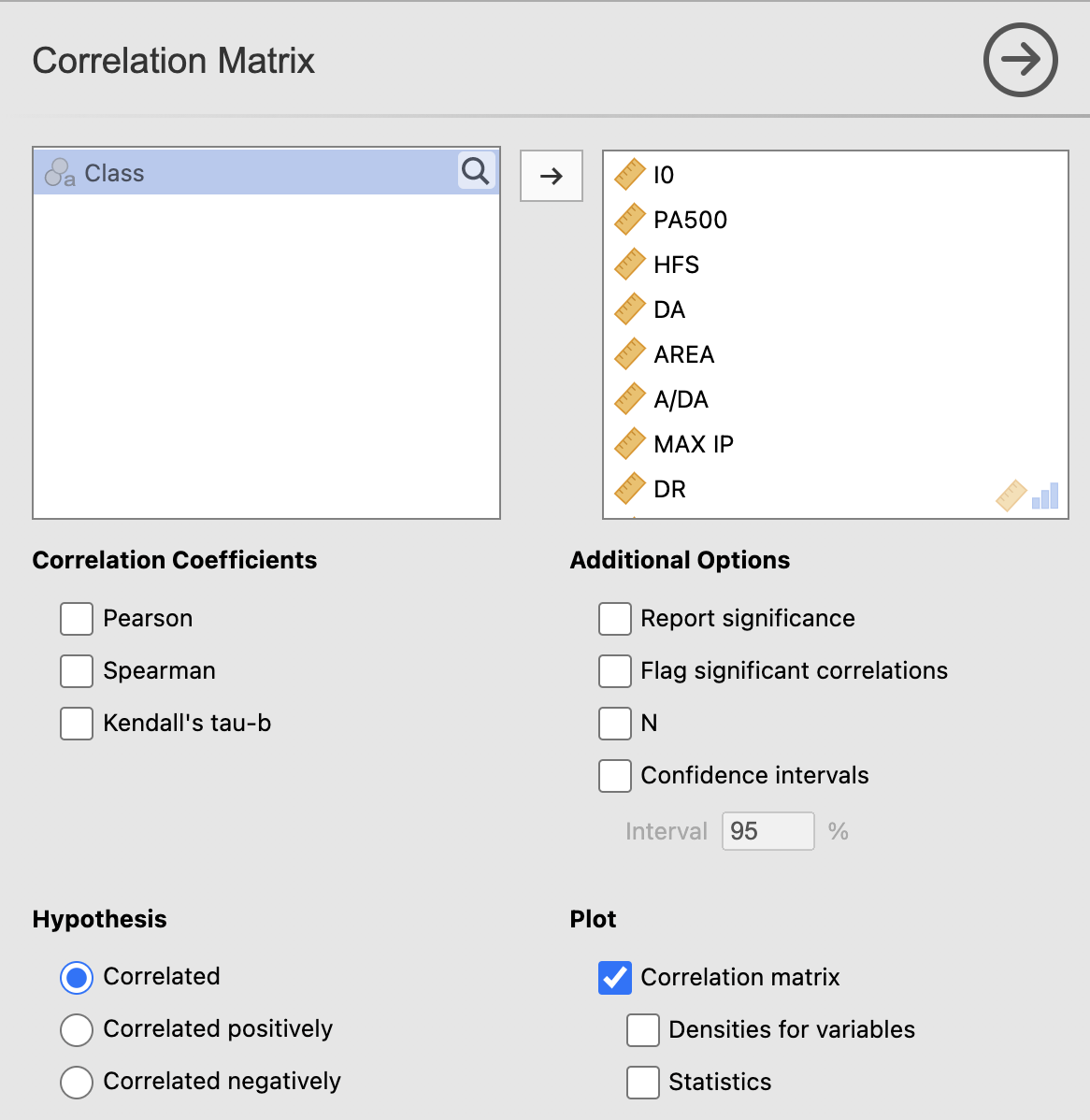
Analyses -> Regression -> Correlation Matrix. Za analizo izberemo vse spremenljivke: I0, PA500, HFS, DA, AREA, A/DA, MAX IP, DR, P ter pod Correlation Coefficients označimo korelacijska koeficienta Pearson in Spearman.
V rezultatskem oknu dobimo izračun korelacijskih koeficientov. P-vrednost nam pove, če je korelacija statistično značilno različna od 0, vrednost korelacije pa koliko sta spremenljivki povezani oz. korelirani.
Ugotovimo lahko, da je spremenljivka I0 najbolj korelirana s spremenljivko P, saj je vrednost Pearsonovega koeficienta korelacije enaka 0.989 (popolna povezanost). Vrednost je pozitivna, kar pomeni, da če ena spremenljivka narašča, potem tudi druga narašča. V primeru negativnega korelacijskega koeficienta pomeni, da ko ena spremenljivka narašča, druga pada in obratno.
Po Pearsonovem koeficientu korelacije spremenljivka I0 dobro korelira z naslednjimi spremenljivkami: DA, MAX IP in DR (vrednost približno 0.75 ali več). Spremenljivka PA500 je najbolj korelirana s spremenljivko HFS (0.509). Vse omenjene korelacije so statistično značilne.
Pri izračunih koeficienta testiramo še ničto hipotezo: Vrednost korelacije je enaka nič.
V primeru, ko je p-vrednost večja od 0.05 ničto hipotezo sprejmemo, ko pa so p-vrednosti manjše od 0.05 lahko ugotovimo, da je korelacija med spremenljivkami statistično značilno različna od nič, kar pomeni povezanost spremenljivk.
Poglejmo še vrednosti Spearmanovih koeficientov korelacije:
Če gledamo korelacije spremenljivke I0 v tej tabeli z ostalimi spremenljivkami, lahko ugotovimo, da je s spremenljivko I0 dobro povezana tudi spremenljivka AREA. Gre torej za nelinearno povezanost, v našem primeru predvsem zaradi tega, kar smo že opazili pri grafu medsebojne povezanosti, da imamo sicer linearno povezanost, vendar z eno močno odstopajočo točko, kar na Spearmanovo korelacijo, kjer primerjamo med sabo vrstni red meritev, ne vpliva.
6.2 Linearna regresija
Postopek reševanja
Modelirali bomo težo novorojenčka FTW s spremenljivkami BPD, CP, AP in FL. Zanima nas, ali lahko iz teh parametrov izračunamo težo novorojenčka. Povezave med parametri bomo ugotavljali ločeno, torej povezavo med BPD in FTW, CP in FTW, AP in FTW ter FL in FTW.
Odpremo ustrezne podatke v Jamovi: Open in izberemo datoteko Foetal Weight.xlsx. Popravimo podatke tako, da prvo vrstico v Data, ki je brez vrednosti, izbrišemo z desnim klikom na vrstico in izbiro Delete Row.
Najprej bomo težo novorojenčka FTW modelirali s spremenljivko BPD.
Narisali bomo graf medsebojnega raztrosa podatkov, kjer bomo ugotavljali povezavo med BPD in težo novorojenčka FTW z ukazom Analyses -> Exploration -> Scatterplot.
Primerjali bomo spremenljivko BPD glede na spremenljivko FTW. Uporabili bomo graf medsebojnega raztrosa podatkov (angl. Scatterplot). Spremenljivko BPD vnesemo na x-os, spremenljivko FTW pa na y-os. V desnem oknu Results se izriše graf raztrosa podatkov.
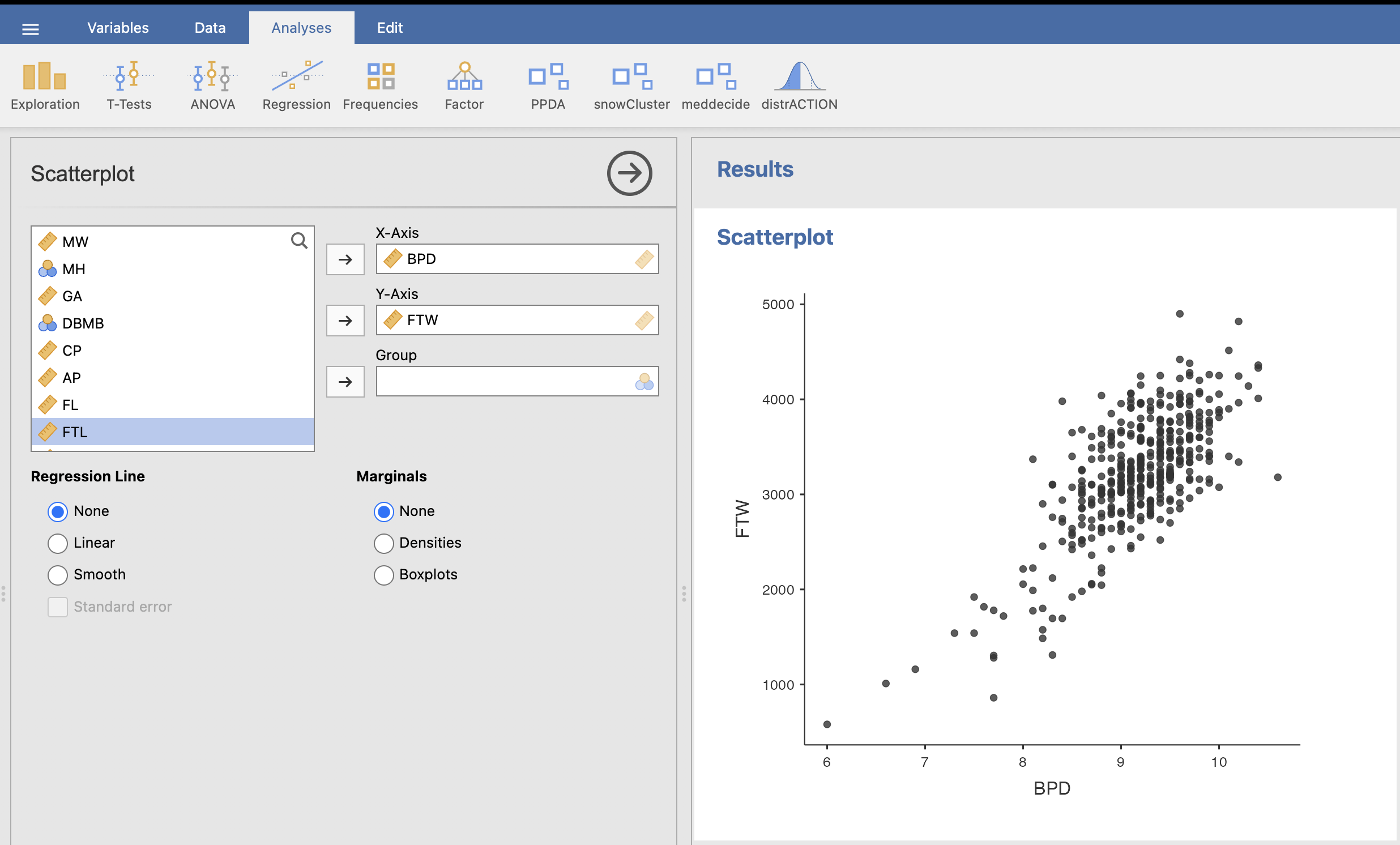
Ugotovimo, da večji kot je BPD, večji je tudi FTW. Meritve so na desni strani grafa bolj gosto narisane, ker je tam večje število meritev.
Sedaj bomo zgradili model linearne regresije, pri čemer bo FTW odzivna spremenljivka BPD pa opisna spremenljivka. Izgradili bomo model: \[FTW\sim β_{0} + β_{1}BPD + \varepsilon \]
Model bomo izračunali po principu linearne regresije. Ko bomo poznali koeficiente \(\beta_{0}\) in \(\beta_{1}\), bomo lahko napovedovali težo novorojenčka FTW z BPD.
To storimo z ukazom Analyses -> Regression -> Linear Regression.
Za odvisno spremenljivko (Dependent Variable) izberemo FTW, za opisno (Covariates) pa BPD. Pod razdelkom Model Fit izberemo izpis Adjusted R square in še pri možnosti Overall Model Test izberemo izračun F test za ugotavljanje statistične značilnosti našega modela.
V oknu Results se nam izrišeta dve tabeli.
Iz tabele Model Fit Measures ugotovimo, da je izračunani model statistično značilen, saj je p < 0.001. Iz te tabele razberemo tudi determinacijski koeficient R2 (Adjusted R Square), ki je v tem primeru 0.533. To pomeni, da naš model z BPD opiše 53.3 % variance FTW.
Iz tabele Model Coefficients – FTW lahko razberemo koeficiente β našega modela: β0 = −4229.1, β1 = 813.3 s p < 0.001, kar pomeni da je β1 statistično značilno različen od 0 oziroma, da je meritev BPD pomemben faktor za FTW.
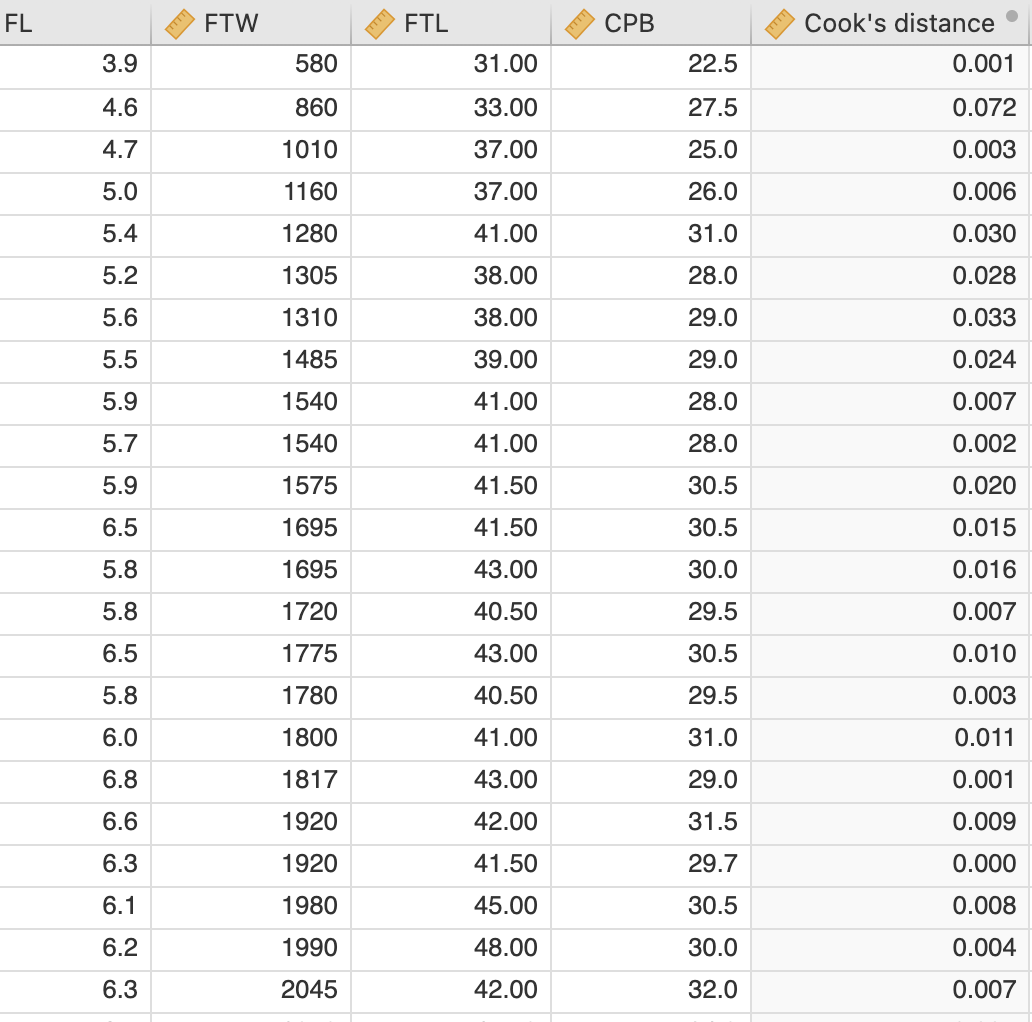
Za dodatno robustnost modela izračunamo še Cookovo razdaljo, ki pokaže, katere meritve pomembno vplivajo na izračun modela. Pod razdelkom Save izberemo Cook’s distance. V zavihku Data se izpiše nova spremenljivka Cookove razdalje (Cook’s distance).
Narišemo graf raztrosa Cookove razdalje glede na BPD z ukazom Analyses -> Exploration -> Scatterplot. Spremenljivko BPD prenesemo na x-os, spremenljivko Cook’s distance pa na y-os. V rezultatskem oknu se nam izriše naslednji graf.
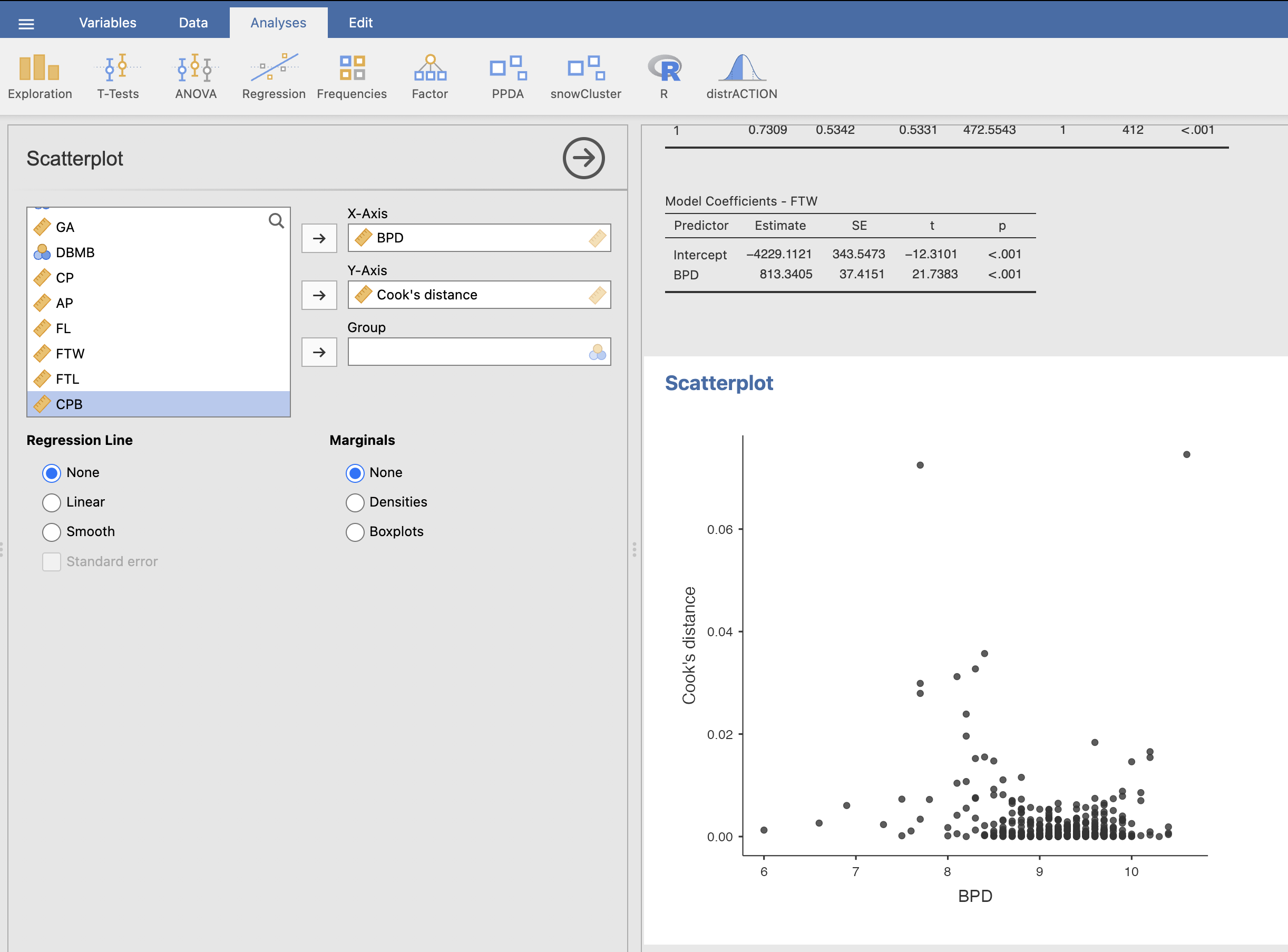
Iz grafa ugotovimo, da odstopata dve meritvi (meritvi, ki sta na grafu najvišje). Ti dve meritvi najbolj vplivata na kakovost modela, zato ju bomo izločili iz podatkov in ponovno izvedli izračun modela. Nov model bo bolj robusten, to pomeni, da bo boljše napovedoval težo novorojenčka FTW v primeru pričakovanih meritev BPD, ne pa pri ekstremnih vrednostih BPD.
Cookova razdalja dveh odstopajočih meritev je glede na graf večja od 0.06. Meritvi bomo odstranili iz izračuna z uporabo ustreznega filtra. Ker je spremenljivka Cook’s distance izračunana iz naših podatkov in je na njih vezana, je potrebno spremenljivko kopirati in ustvariti spremenljivko Cookova razdalja.
Zdaj bomo lahko uporabili ustrezni filter z izbiro Filters. Izberemo pogoj, kot je prikazano na spodnji sliki:
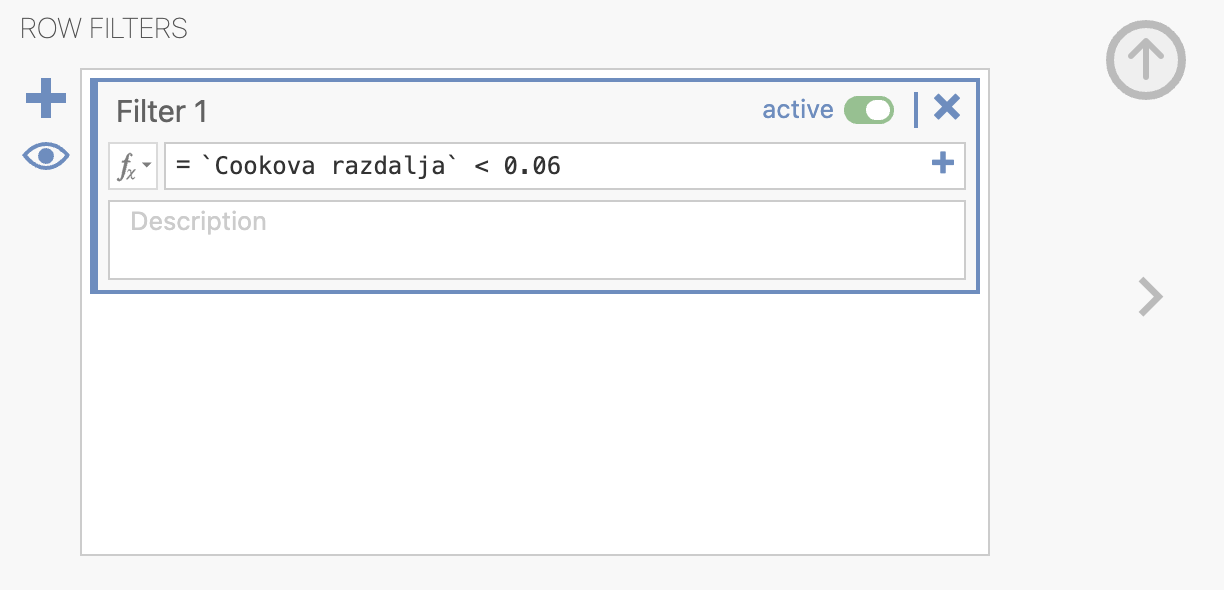
V Data lahko vidimo, da 2. in 183. meritev ne bosta upoštevani v ponovni izračun modela.
Izračunajmo nov, popravljen model z ukazom Analyses -> Regression -> Linear Regression, kjer je FTW odzivna spremenljivka, BPD pa opisna spremenljivka.
Parametre iz dobljenih rezultatskih tabel prepišemo v spodnjo tabelo.
| \(β_1\) | p-vrednost koeficienta | p-vrednost modela | \(R^2\) | |
|---|---|---|---|---|
| BPD | 813.3 | < 0.001 | < 0.001 | 0.533 |
| Popravljen model z BPD | 813.5 | < 0.001 | < 0.001 | 0.535 |
Pri popravljenem modelu se rezultati spremenijo le malenkostno, saj imamo veliko število meritev in če odstranimo dve meritvi z malimi vrednostmi Cookove razdalje, modela ne spremenimo veliko.
Enak postopek linearne regresije ponovimo še za meritve CP, AP in FL posebej.
Rezultati modeliranja so v spodnji tabeli. Modeli niso popravljeni glede na Cookovo razdaljo.
| \(β_1\) | p-vrednost koeficienta | p-vrednost modela | \(R^2\) | |
|---|---|---|---|---|
| CP | 253.8 | < 0.001 | < 0.001 | 0.551 |
| AP | 173.4 | < 0.001 | < 0.001 | 0.716 |
| FL | 895.7 | < 0.001 | < 0.001 | 0.573 |
Vsak parameter posamično je dober napovedovalec teže novorojenčka (\(β_1\) je statistično značilno različen od 0). Meritev AP je med njimi najboljša, saj ima najvišji determinacijski koeficient (71.6 %).
6.3 Multipla linearna regresija
Postopek reševanja
Podatke pripravimo kot pri vaji iz pog. 6.2 v začetnem koraku.
Z izbranimi parametri (BPD, CP, AP, FL) bi radi napovedovali težo novorojenčka – FTW.
\[FTW\ \sim\ BPD + CP + AP + FL\]
Spremenljivko FTW želimo napovedati s spremenljivkami FL, AP, CP in BPD skupaj, zato izdelamo model multiple linearne regresije z ukazom Analyses -> Regression -> Linear Regression.
Kot odzivno spremenljivko (Dependent Variable) izberemo FTW, kot opisne spremenljivke (Covariates) izberemo FL, AP, CP, BPD. Pod razdelkom Model Fit izberemo izpis Adjusted R square in še pri možnosti Overall Model Test izberemo izračun F test za ugotavljanje statistične značilnosti našega modela. Model linearne regresije se izračuna v desnem rezultatskem oknu.
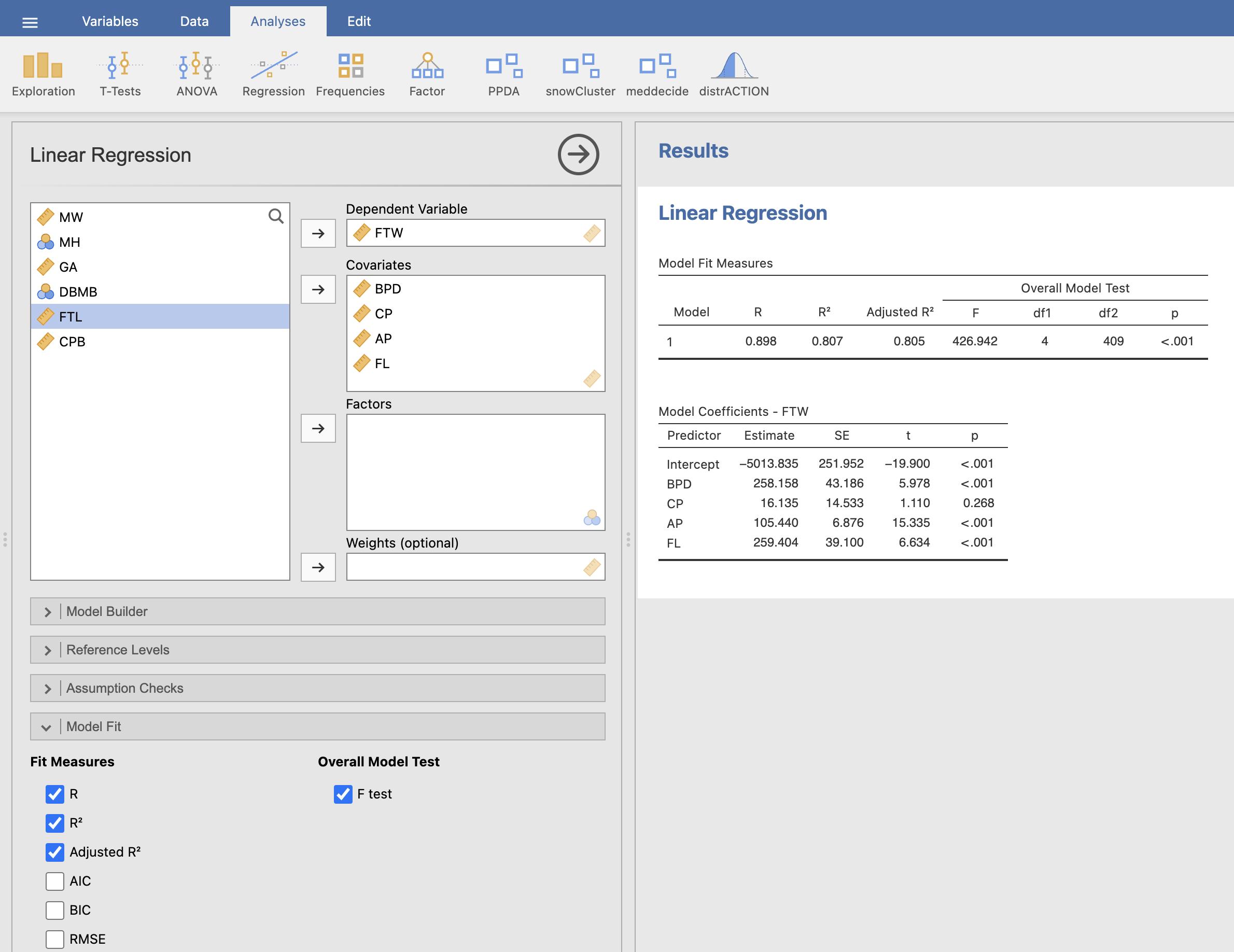
Tabela Model Fit Measures nam pove, kakšen je determinacijski koeficient (Adjusted R2) regresijskega modela. P-vrednost pri Overall Model Test nam pove, ali je regresijski model statistično ustrezen. V tabeli Model Coefficients - FTW so izračunani koeficienti β in pripadajoče p-vrednosti za posamezno spremenljivko.
Na podlagi teh rezultatov lahko sestavimo spodnjo tabelo:
| β | p-vrednost koeficienta | p-vrednost modela | R2 | |
|---|---|---|---|---|
| BPD | 258.2 | < 0.001 | < 0.001 | 0.805 |
| CP | 16.1 | 0.268 | ||
| AP | 105.4 | < 0.001 | ||
| FL | 259.4 | < 0.001 |
Rezultati nam kažejo, da je model s štirimi spremenljivkami (BPD, CP, AP in FL) statistično ustrezen (F = 426.9, p < 0.001). Determinacijski koeficient je enak 0.805, kar pomeni da z njim opišemo 80.5 % variance FTW. Vrednosti β koeficientov spremenljivk BPD, AP in FL so statistično značilno različne od nič (p < 0.001), β koeficient spremenljivke CP pa ni statistično značilno različen od nič (p = 0.268) in so s tem meritve CP statistično nepomembne za naš model.
Izračunali bomo še korelacije med parametri BPD, CP, AP in FL z ukazom Analyses -> Regression > Correlation Matrix.
Kot spremenljivke izberemo parametre BPD, CP, AP in FL ter pod Correlation Coefficients izberemo izračun Pearsonovega korelacijskega koeficienta. V desnem oknu dobimo tabelo z rezultati.
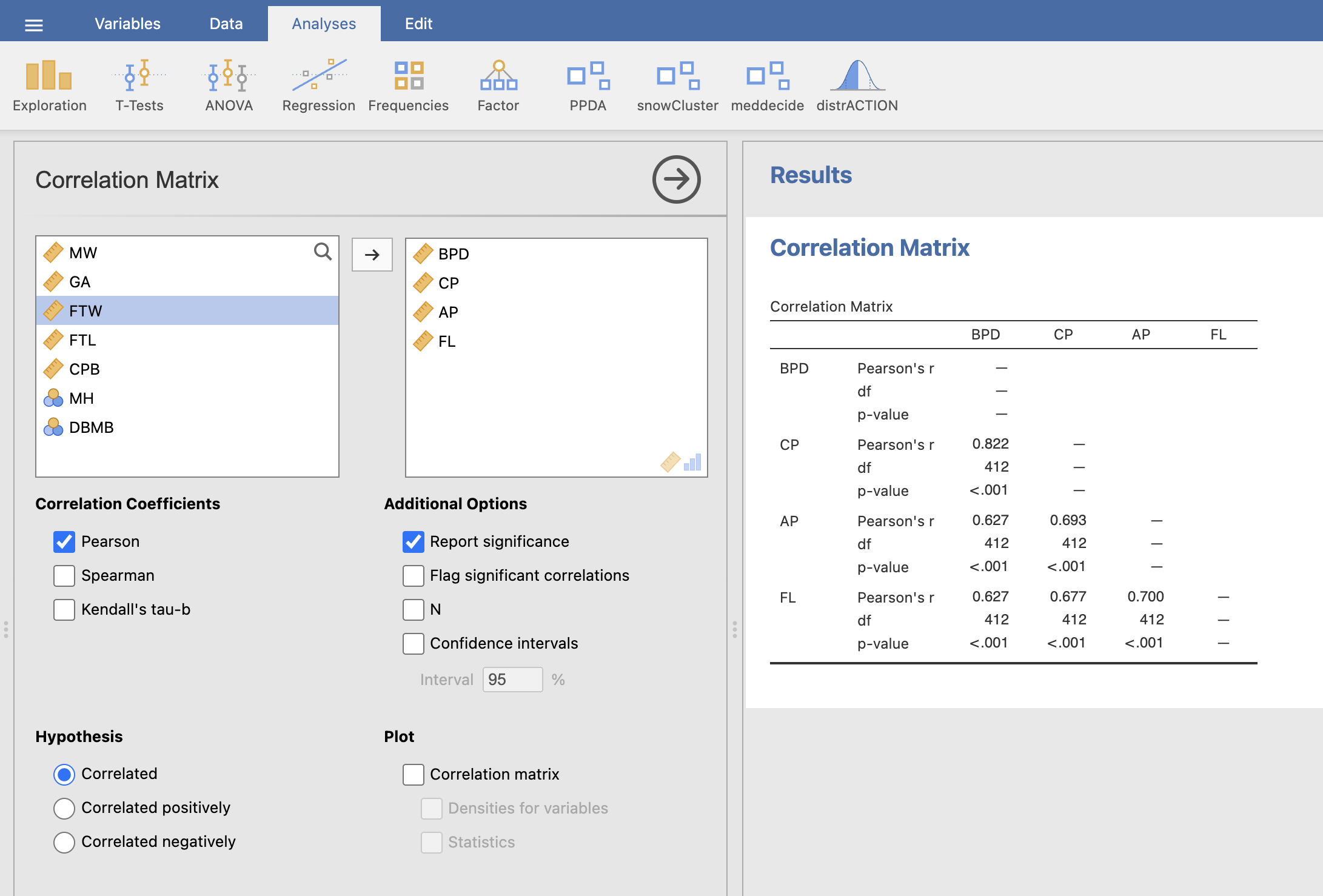
Ugotovimo, da je BPD močno koreliran s CP (0.82), kar pomeni, da ju lahko v modelu obravnavamo kot kofaktorja. To pomeni, da če eno spremenljivko vključimo v model, ni potrebno druge, saj spremenljivke, ki so med seboj korelirane, ne izboljšajo modela.
6.4 Multipla linearna regresija – koračna metoda (programska koda v R)
Postopek reševanja
Podatke pripravimo kot v začetnem koraku pri vaji iz pog. 6.2.
Spremenljivko FTW želimo napovedati s spremenljivkami FL, AP, CP in BPD, vendar v tem primeru želimo zgraditi model po korakih, kjer dodajamo v model po vrsti tiste spremenljivke, ki največ prispevajo k napovedi modela.
Kriterijev za merjenje, kateri model je boljši, je več. Najbolj pogosto se uporablja kriterij AIC (Akaike Information Criteria) (Venables and Ripley 2002), ki ga bomo uporabili tudi mi v naši analizi. Po tem kriteriju je boljši tisti model, ki ima nižje vrednosti AIC.
Ker tovrstnega modeliranja ne moremo izvajati neposredno v okolju Jamovi, bomo uporabili programski jezik R, na katerem sloni tudi Jamovi. Za uporabo programskega jezika R v Jamovi je potrebno najprej namestiti modul Rj, ki ga najdemo v knjižnici modulov:
Po namestitvi se nam nov modul (R) pokaže v orodni vrstici programa Jamovi:
Ta modul nam omogoča, da lahko pišemo programsko kodo R neposredno v programu Jamovi. V našem primeru bomo uporabili R za izvedbo koračne metode na naših podatkih.
Koračna metoda modelira regresijski model tako, da v vsakem koraku v model vstavi po eno spremenljivko in sicer tako, da na vsakem koraku izbere tisto spremenljivko, katere model ima po kriteriju AIC najmanjšo vrednost. Gradnja modela se konča, ko z dodajanjem ne moremo več znižati vrednosti AIC oziroma ko imamo v modelu že vse spremenljivke. Ta način se imenuje koračna metoda z dodajanjem spremenljivk (ang. forward). Obstaja pa še način, ko imamo v začetnem modelu vse spremenljivke, pa jih po korakih odvzemamo, dokler znižujemo vrednost AIC (ang. backward). Mi bomo uporabili prvi način grajenja modela.
Za to v modulu R izberemo Rj editor in vpišemo naslednjo kodo v jeziku R:
Kodo, ki smo jo napisali v urejevalniku Rj, lahko poženemo z zelenim trikotnim gumbom desno zgoraj (glej spodnjo sliko). Če je koda pravilna, se nam v desnem oknu izpišejo rezultati, ki so posledica ukazov v levem oknu.
Komentar programske kode v R:
V primeru koračne metode je potrebno najprej definirati začetni in končni model. Začetni model je običajno model brez spremenljivk, v našem primeru \(FTW \sim 1\) pomeni model \(FTW = \beta_0 + \epsilon\) oziroma model brez spremenljivk.
To v R izvedemo s spodnjim ukazom lm na naših podatkih data in potem še izpišemo osnovne statistike tega modela z ukazom summary:
# Začetni model brez spremenljivk
empty_mod <- lm(FTW ~ 1, data=data)
# Statistika modela
summary(empty_mod)Končni model je model z vsemi spremenljivkami vključenimi v modeliranje
\[FTW \sim BPD + FL + AP + CP \] To v R izvedemo s spodnjim ukazom lm na naših podatkih data in potem še izpišemo osnovne statistike tega modela z ukazom summary:
# Končni model z vsemi spremenljivkami
full_mod <- lm(FTW ~ BPD + FL + AP + CP, data=data)
# Statistika modela
summary(full_mod)Koračno metodo modeliranja izvedemo z ukazom step, kjer podamo kot prvi argument začetni model empty_mod in končni model full_mod v argumentu scope. Pri tem pa še definiramo smer grajenja modela, v našem primeru je grajenje z dodajanjem spremenljivk, kar definiramo z argumentom direction="forward":
# Koračna metoda: forward
# Štartamo z empty_mod in končamo s full_mod
mod = step(empty_mod, direction = "forward", scope=formula(full_mod))
# Statistika modela
summary(mod)V oknu rezultatov se po izvedbi kode izpišejo rezultati analize, kot je prikazano na spodnji sliki.
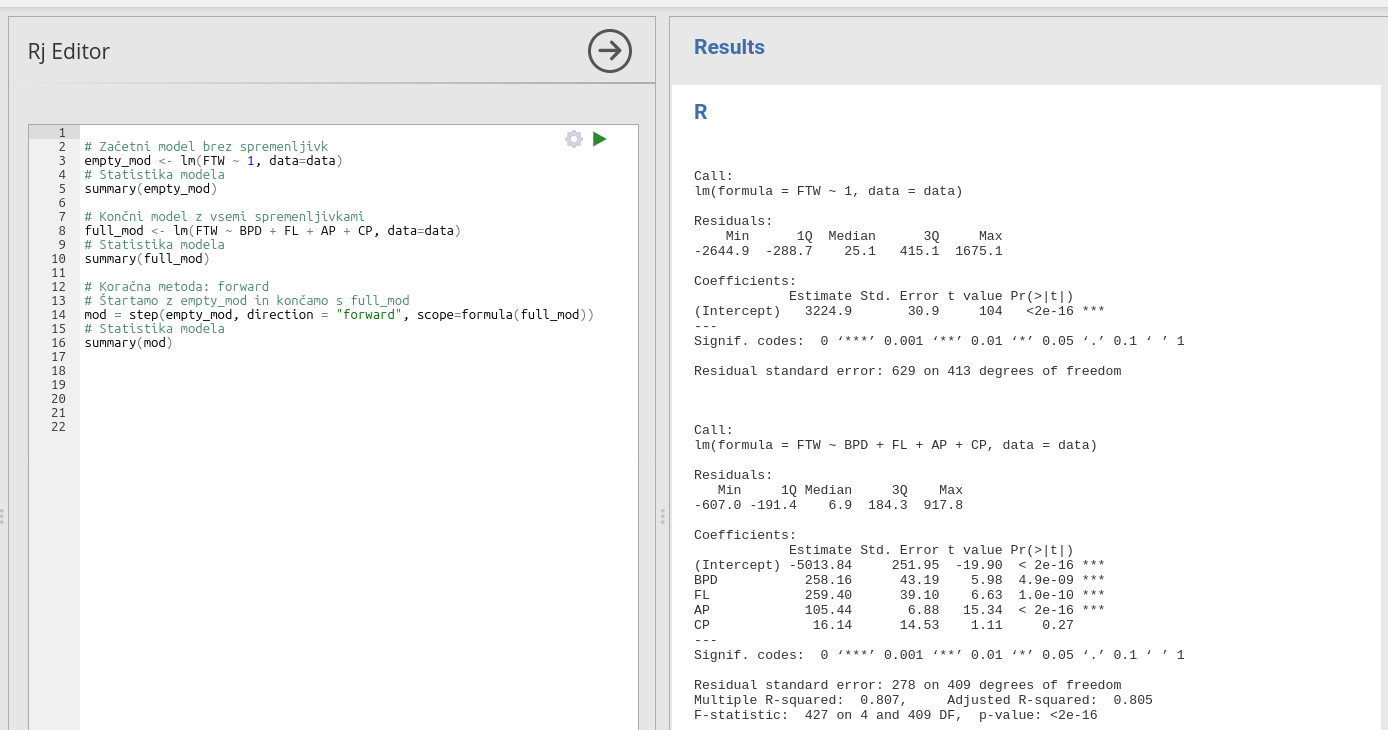
Komentar rezultatov:
Najprej se izpiše statistika začetnega modela brez spremenljivk empty_mod:
Call:
lm(formula = FTW ~ 1, data = data)
Residuals:
Min 1Q Median 3Q Max
-2644.9 -288.7 25.1 415.1 1675.1
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3224.9 30.9 104 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 629 on 413 degrees of freedomPotem izpišemo statistiko modela z vsemi spremenljivkami full_mod. Rezultati statistike modela so enaki kot pri prejšnji nalogi iz pog. 6.3, ko smo izvajali multiplo linearno regresijo z vsemi spremenljivkami. Dobili smo enake rezultate, in sicer spremenljivke BPD, FL in AP so statistično pomembne v modelu, CP pa ne. Determinacijski koeficient modela \(R^2 = 0.805\), F-koeficient je 427 in je statistično značilen s \(p<2e^{-16}\)
Call:
lm(formula = FTW ~ BPD + FL + AP + CP, data = data)
Residuals:
Min 1Q Median 3Q Max
-607.0 -191.4 6.9 184.3 917.8
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -5013.84 251.95 -19.90 < 2e-16 ***
BPD 258.16 43.19 5.98 4.9e-09 ***
FL 259.40 39.10 6.63 1.0e-10 ***
AP 105.44 6.88 15.34 < 2e-16 ***
CP 16.14 14.53 1.11 0.27
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 278 on 409 degrees of freedom
Multiple R-squared: 0.807, Adjusted R-squared: 0.805
F-statistic: 427 on 4 and 409 DF, p-value: <2e-16V nadaljevanju pa se izpisujejo rezultati vključevanja spremenljivk v modele, ki jih gradimo po korakih od modela brez spremenljivk empty_mod do modela z vsemi spremenljivkami full_mod.
Start: AIC=5336
FTW ~ 1
Df Sum of Sq RSS AIC
+ AP 1 1.17e+08 4.62e+07 4816
+ FL 1 9.36e+07 6.96e+07 4985
+ CP 1 9.01e+07 7.31e+07 5006
+ BPD 1 8.72e+07 7.60e+07 5022
<none> 1.63e+08 5336
Step: AIC=4816
FTW ~ AP
Df Sum of Sq RSS AIC
+ BPD 1 10791230 35414962 4708
+ FL 1 8654104 37552088 4732
+ CP 1 7703332 38502860 4742
<none> 46206191 4816
Step: AIC=4708
FTW ~ AP + BPD
Df Sum of Sq RSS AIC
+ FL 1 3791735 31623226 4663
+ CP 1 493852 34921110 4704
<none> 35414962 4708
Step: AIC=4663
FTW ~ AP + BPD + FL
Df Sum of Sq RSS AIC
<none> 31623226 4663
+ CP 1 95024 31528202 4664
Call:
lm(formula = FTW ~ AP + BPD + FL, data = data)
Residuals:
Min 1Q Median 3Q Max
-607.5 -190.1 -1.2 189.5 922.3
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -4900.24 230.31 -21.28 < 2e-16 ***
AP 107.48 6.63 16.22 < 2e-16 ***
BPD 289.13 32.98 8.77 < 2e-16 ***
FL 268.35 38.27 7.01 9.8e-12 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 278 on 410 degrees of freedom
Multiple R-squared: 0.806, Adjusted R-squared: 0.805
F-statistic: 569 on 3 and 410 DF, p-value: <2e-16Pred vsakim korakom se izpiše vrednost kriterija AIC. V prvem koraku, ko imamo model \(FTW\sim 1\) je \(AIC=5336\), spodaj pa so navedene spremenljivke AP, FL, CP, BPD in <none> z izračunanimi vrednostmi AIC, če spremenljivko dodamo v model. Tako ima spr. AP vrednost AIC=4816, FL vrednost AIC=4985, CP vrednost AIC=5006, BPD vrednost AIC=5022 in model brez spr. <none> vrednost AIC=5366. V vsakem koraku dodamo v model tisto spremenljivko, ki najbolj zniža vrednost AIC. Tako v prvem koraku dodamo spr. AP z vrednost AIC=4816, ki je najmanjša med vsemi ostalimi vrednostmi AIC. Tako dobimo v drugem koraku model \(FTW \sim AP\) in ponovno izračunamo vrednosti AIC za ostale spremenljivke, če jih dodajamo v model. Tako v drugem koraku izberemo spr. BPD z vrednostjo AIC=4708 in dobimo model v tretjem koraku \(FTW \sim AP + BPD\). V tretjem koraku je spr. z najnižjo AIC vrednostjo spr. FL ( AIC=4663 ) in dobimo model \(FTW \sim AP + BPD + FL\). V četrtem koraku je bolje dodati spr. <none>, saj ima nižjo vrednost AIC=4663 kot spr. CP z AIC=4664. To pomeni, da na tem koraku zaustavimo postopek, saj se z dodajanjem novih spr. vrednosti AIC ne nižajo več. Torej je končni model \(FTW \sim AP + BPD + FL\) brez spr. CP.
V zadnjem delu se izpiše še statistika končnega modela \(FTW \sim AP + BPD + FL\), zgrajenega po koračnem postopku s kriterijem AIC. Vse tri spremenljivke v modelu so statistično pomembne. Determinacijski koeficient modela \(R^2 = 0.805\), F-koeficient je 569 in je statistično značilen s \(p<2e^{-16}\). To je naš končni model.
Gradnja modela po korakih nam tudi omogoča, da razvrstimo spremenljivke po pomembnosti vplivanja na odzivno spr. FTW. Prva spr., ki je bila dodana modelu je spr. AP, potem BPD in nato še FL, spr. CP pa ni pomembna za napovedovanje FTW. Končni model tako ne vsebuje spremenljivke CP, kar smo pokazali že v prejšnji nalogi, ko smo ugotovili, da sta spremenljivki BPD in CP kofaktorja.
6.5 Multipla linearna regresija – dodajanje nelinearnih členov – minimizacija modela s koračno metodo (programska koda v R)
Postopek reševanja
Podatke pripravimo kot pri vaji iz pog. 6.2 v koraku 1.
Gradnjo modela multiple linearne regresije bomo izvajali na podoben način kot pri prejšnji vaji iz pog. 6.4. Tu bomo dodali nove spremenljivke, kjer bomo dodali kvadratne člene in medsebojne produkte spremenljivk. Končni model, ki ga bomo minimizirali, je naslednji model:
\[ FTW \sim BPD + FL + AP + CP + \] \[ BPD^2 + AP^2 + CP^2 + FL^2 + \] \[ BPD\cdot CP + BPD\cdot AP + BPD \cdot FL + CP \cdot AP + CP \cdot FL + AP\cdot FL \]
Za to moramo najprej tvoriti nove spremenljivke ter nato po koračni metodi zgraditi minimalni model.
To naredimo v Jamovi tako, da v modulu R izberemo Rj editor +. Rj editor + se razlikuje od Rj editor, da lahko v Rj editor + izberemo samo spremenljivke, s katerimi bomo delali in ko kreiramo nove spremenljivke, se nam te shranijo med našimi podatki. Tako izberemo spremenljivke BPD, CP, AP, FL in FTW, s katerimi bomo delali v Rj editor +.
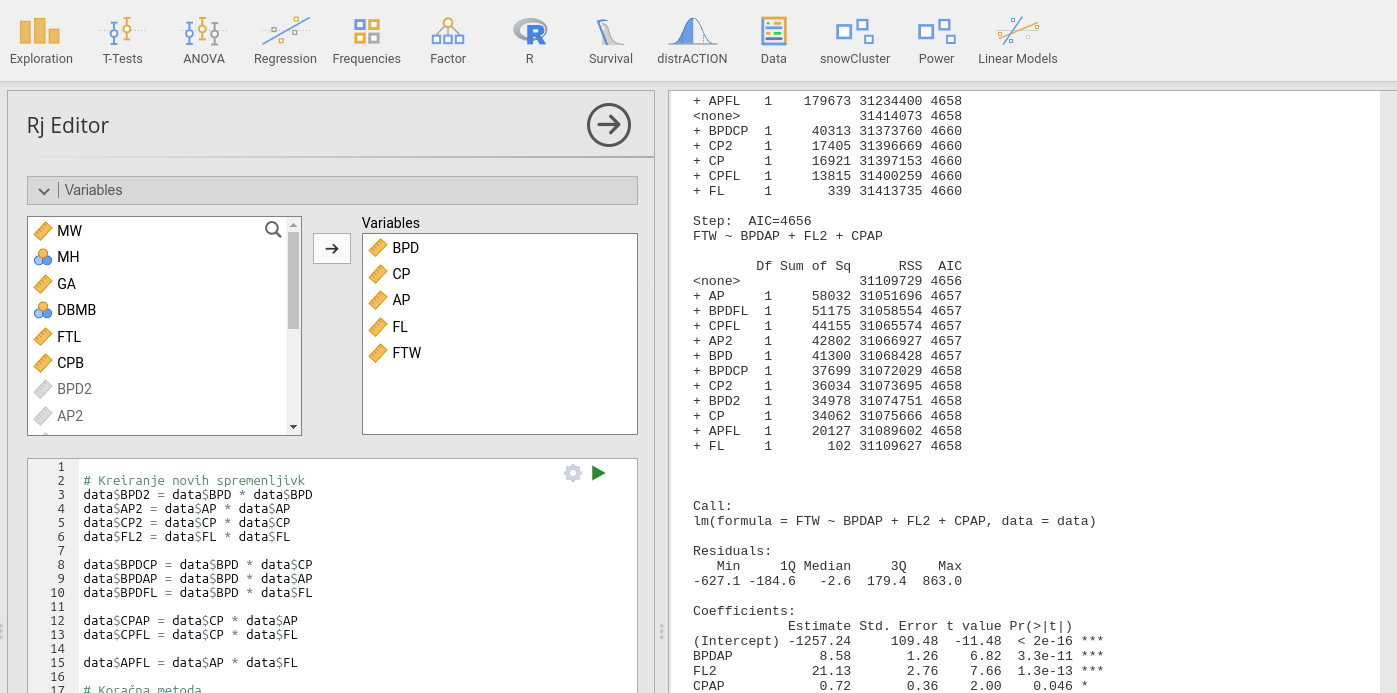
In vpišemo naslednjo kodo v jeziku R:
# Kreiranje novih spremenljivk
data$BPD2 = data$BPD * data$BPD
data$AP2 = data$AP * data$AP
data$CP2 = data$CP * data$CP
data$FL2 = data$FL * data$FL
data$BPDCP = data$BPD * data$CP
data$BPDAP = data$BPD * data$AP
data$BPDFL = data$BPD * data$FL
data$CPAP = data$CP * data$AP
data$CPFL = data$CP * data$FL
data$APFL = data$AP * data$FL
# Koračna metoda
# Začetni model brez spremenljivk
empty_mod <- lm(FTW ~ 1, data=data)
summary(empty_mod)
# Končni model z vsemi spremenljivkami
full_mod <- lm(FTW ~ BPD + FL + AP + CP +
BPD2 + AP2 + CP2 + FL2 +
BPDCP + BPDAP + BPDFL + CPAP + CPFL + APFL, data=data)
summary(full_mod)
# koračna metoda: forward
mod2 = step(empty_mod, direction = "forward", scope=formula(full_mod))
summary(mod2)
# Končni model
mod3 <- lm(FTW ~ BPDAP + FL2, data=data)
summary(mod3)Komentar programske kode v R:
Najprej izračunamo nove spremenljivke \(BPD2 = BPD\cdot BPD\), \(AP2 = AP\cdot AP\), \(CP2 = CP\cdot CP\), \(FL2 = FL\cdot FL\), \(BPDCP = BPD\cdot CP\), \(BPDAP = BPD\cdot AP\), \(BPDFL = BPD\cdot FL\), \(CPAP = CP\cdot AP\), \(CPFL = CP\cdot FL\), \(APFL = AP\cdot FL\). To naredimo s spodnjimi ukazi.
# Kreiranje novih spremenljivk
data$BPD2 = data$BPD * data$BPD
data$AP2 = data$AP * data$AP
data$CP2 = data$CP * data$CP
data$FL2 = data$FL * data$FL
data$BPDCP = data$BPD * data$CP
data$BPDAP = data$BPD * data$AP
data$BPDFL = data$BPD * data$FL
data$CPAP = data$CP * data$AP
data$CPFL = data$CP * data$FL
data$APFL = data$AP * data$FLPotem pa izvedemo koračno metodo grajenja modela z dodajanjem novih spremenljivk, podobno kot pri prejšnji nalogi iz pog. 6.4. Najprej definiramo model brez spremenljivk empty_mod in končni model full_mod z vsemi spremenljivkami. Pri obeh modelih tudi izpišemo statistike modela (ukaz summary). Nato pa izvedemo ukaz step, kjer podobno kot pri prejšnji nalogi povemo, da štartamo gradnjo modela z empty_mod in končamo pri full_mod, pri čemer gradimo model z dodajanjem novih spremenljivk v model po metodi forward. Zgrajeni model se shrani v mod2 in ga potem tudi izpišemo s summary. Končni model je sestavljen samo iz dveh spremenljivk BPDAP in FL2 in tega izračunamo v mod3 ter ga predstavimo z ukazom summary.
# Koračna metoda
# Začetni model brez spremenljivk
empty_mod <- lm(FTW ~ 1, data=data)
summary(empty_mod)
# Končni model z vsemi spremenljivkami
full_mod <- lm(FTW ~ BPD + FL + AP + CP +
BPD2 + AP2 + CP2 + FL2 +
BPDCP + BPDAP + BPDFL + CPAP + CPFL + APFL, data=data)
summary(full_mod)
# koračna metoda: forward
mod2 = step(empty_mod, direction = "forward", scope=formula(full_mod))
summary(mod2)
# Končni model
mod3 <- lm(FTW ~ BPDAP + FL2, data=data)
summary(mod3)V oknu rezultatov se po izvedbi kode izpišejo rezultati analize, kot je prikazano na spodnji sliki.
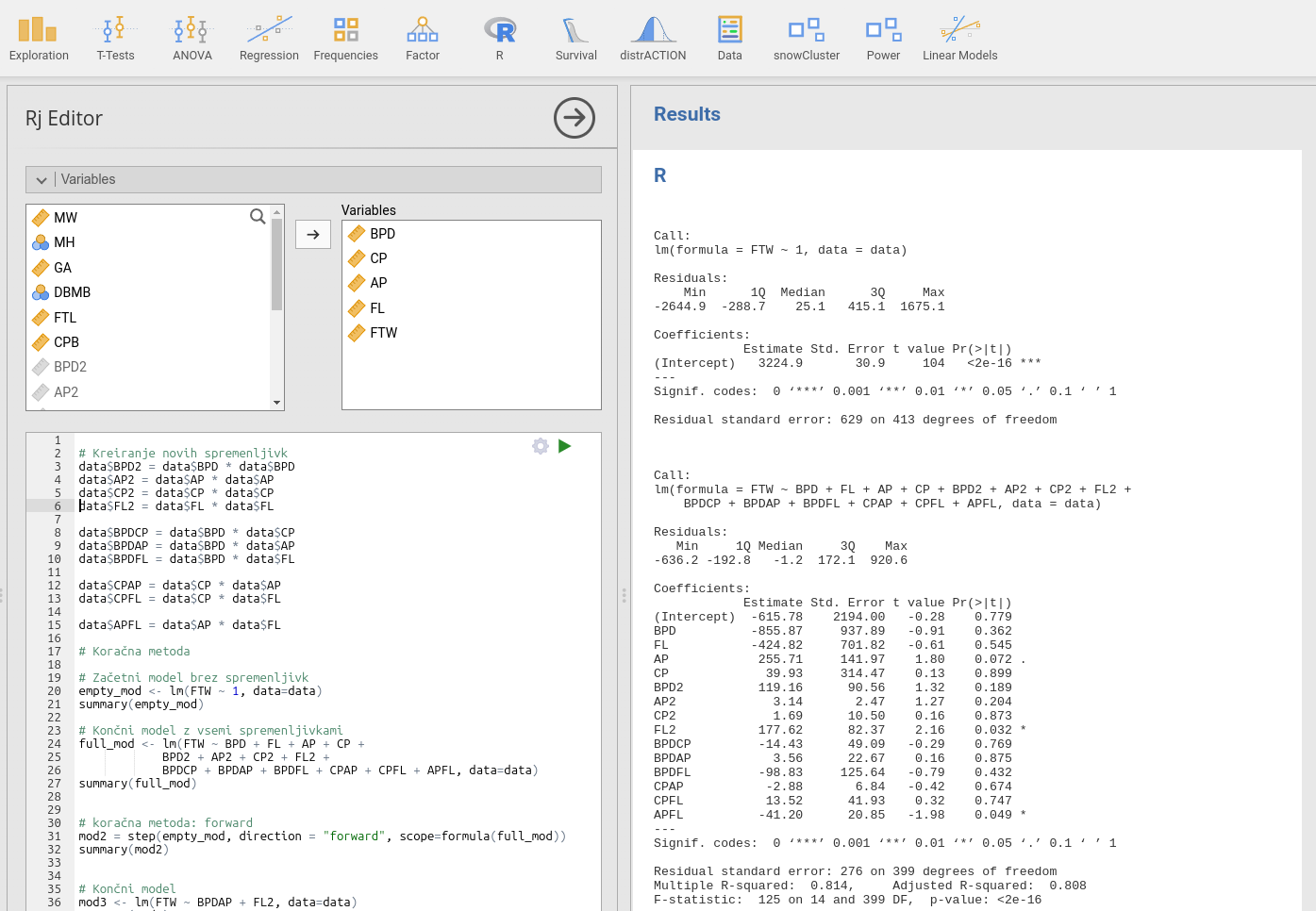
Komentar rezultatov:
Najprej se izpiše statistika začetnega modela brez spremenljivk empty_mod:
Call:
lm(formula = FTW ~ 1, data = data)
Residuals:
Min 1Q Median 3Q Max
-2644.9 -288.7 25.1 415.1 1675.1
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3224.9 30.9 104 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 629 on 413 degrees of freedomPotem izpišemo statistiko modela z vsemi spremenljivkami full_mod. Tu lahko ugotovimo, da imata samo dve spremenljivki koeficiente statistično različne od 0 in to sta FL2 in APFL. Ampak to ni naš končni model, saj bomo v nadaljevanju zgradili model po korakih.
Call:
lm(formula = FTW ~ BPD + FL + AP + CP + BPD2 + AP2 + CP2 + FL2 +
BPDCP + BPDAP + BPDFL + CPAP + CPFL + APFL, data = data)
Residuals:
Min 1Q Median 3Q Max
-636.2 -192.8 -1.2 172.1 920.6
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -615.78 2194.00 -0.28 0.779
BPD -855.87 937.89 -0.91 0.362
FL -424.82 701.82 -0.61 0.545
AP 255.71 141.97 1.80 0.072 .
CP 39.93 314.47 0.13 0.899
BPD2 119.16 90.56 1.32 0.189
AP2 3.14 2.47 1.27 0.204
CP2 1.69 10.50 0.16 0.873
FL2 177.62 82.37 2.16 0.032 *
BPDCP -14.43 49.09 -0.29 0.769
BPDAP 3.56 22.67 0.16 0.875
BPDFL -98.83 125.64 -0.79 0.432
CPAP -2.88 6.84 -0.42 0.674
CPFL 13.52 41.93 0.32 0.747
APFL -41.20 20.85 -1.98 0.049 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 276 on 399 degrees of freedom
Multiple R-squared: 0.814, Adjusted R-squared: 0.808
F-statistic: 125 on 14 and 399 DF, p-value: <2e-16V nadaljevanju se izpisujejo rezultati vključevanja spremenljivk v modele, ki jih gradimo po korakih od modela brez spremenljivk empty_mod do modela z vsemi spremenljivkami full_mod skupaj z AIC vrednostmi:
Start: AIC=5336
FTW ~ 1
Df Sum of Sq RSS AIC
+ BPDAP 1 1.27e+08 3.65e+07 4718
+ APFL 1 1.24e+08 3.92e+07 4747
+ CPAP 1 1.23e+08 3.99e+07 4756
+ AP 1 1.17e+08 4.62e+07 4816
+ AP2 1 1.14e+08 4.92e+07 4842
+ BPDFL 1 1.11e+08 5.21e+07 4866
+ CPFL 1 1.09e+08 5.40e+07 4880
+ BPDCP 1 9.57e+07 6.75e+07 4973
+ FL 1 9.36e+07 6.96e+07 4985
+ FL2 1 9.19e+07 7.13e+07 4995
+ CP 1 9.01e+07 7.31e+07 5006
+ CP2 1 8.83e+07 7.49e+07 5016
+ BPD 1 8.72e+07 7.60e+07 5022
+ BPD2 1 8.52e+07 7.80e+07 5033
<none> 1.63e+08 5336
Step: AIC=4718
FTW ~ BPDAP
Df Sum of Sq RSS AIC
+ FL2 1 5053830 31414073 4658
+ FL 1 4989375 31478529 4659
+ APFL 1 4462044 32005860 4666
+ CPFL 1 4004650 32463254 4672
+ BPDFL 1 2562396 33905508 4690
+ CPAP 1 901036 35566868 4709
+ AP 1 497209 35970695 4714
+ CP 1 333763 36134141 4716
+ AP2 1 278892 36189012 4717
+ CP2 1 273202 36194702 4717
+ BPD2 1 257600 36210304 4717
+ BPD 1 199234 36268670 4718
<none> 36467904 4718
+ BPDCP 1 3 36467901 4720
Step: AIC=4658
FTW ~ BPDAP + FL2
Df Sum of Sq RSS AIC
+ CPAP 1 304345 31109729 4656
+ AP 1 256072 31158002 4657
+ BPDFL 1 243409 31170664 4657
+ AP2 1 229654 31184419 4657
+ BPD 1 219951 31194123 4657
+ BPD2 1 212117 31201956 4657
+ APFL 1 179673 31234400 4658
<none> 31414073 4658
+ BPDCP 1 40313 31373760 4660
+ CP2 1 17405 31396669 4660
+ CP 1 16921 31397153 4660
+ CPFL 1 13815 31400259 4660
+ FL 1 339 31413735 4660
Step: AIC=4656
FTW ~ BPDAP + FL2 + CPAP
Df Sum of Sq RSS AIC
<none> 31109729 4656
+ AP 1 58032 31051696 4657
+ BPDFL 1 51175 31058554 4657
+ CPFL 1 44155 31065574 4657
+ AP2 1 42802 31066927 4657
+ BPD 1 41300 31068428 4657
+ BPDCP 1 37699 31072029 4658
+ CP2 1 36034 31073695 4658
+ BPD2 1 34978 31074751 4658
+ CP 1 34062 31075666 4658
+ APFL 1 20127 31089602 4658
+ FL 1 102 31109627 4658Končni model vključuje samo tri spremenljivke: BPDAP, FL2 in CPAP, ki ga izpišemo v nadaljevanju:
Call:
lm(formula = FTW ~ BPDAP + FL2 + CPAP, data = data)
Residuals:
Min 1Q Median 3Q Max
-627.1 -184.6 -2.6 179.4 863.0
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1257.24 109.48 -11.48 < 2e-16 ***
BPDAP 8.58 1.26 6.82 3.3e-11 ***
FL2 21.13 2.76 7.66 1.3e-13 ***
CPAP 0.72 0.36 2.00 0.046 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 275 on 410 degrees of freedom
Multiple R-squared: 0.809, Adjusted R-squared: 0.808
F-statistic: 580 on 3 and 410 DF, p-value: <2e-16Lahko ugotovimo, da so vse tri spremenljivke v modelu statistično pomembne. Determinacijski koeficient modela \(R^2 = 0.808\), F-koeficient je 580 in je statistično značilen s \(p<2e^{-16}\).
Ker je koeficient pri spr. CPAP mejno statistično različen od 0 (p=0.046), se odločimo, da to spremenljivko odstranimo iz modela in dobimo končni model, ki je prikazan v nadaljevanju:
Call:
lm(formula = FTW ~ BPDAP + FL2, data = data)
Residuals:
Min 1Q Median 3Q Max
-632.1 -191.0 -1.7 179.4 878.6
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1234.642 109.299 -11.30 < 2e-16 ***
BPDAP 10.919 0.478 22.85 < 2e-16 ***
FL2 22.127 2.721 8.13 5.1e-15 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 276 on 411 degrees of freedom
Multiple R-squared: 0.807, Adjusted R-squared: 0.807
F-statistic: 862 on 2 and 411 DF, p-value: <2e-16Tako dobimo končni model \(FTW \sim BPDAP + FL2\). Ugotovimo lahko, da je ta model malce slabši po determinacijskem koeficientu od prejšnjega modela, vendar ima eno spr. manj, kar predstavlja večjo robustnost modela. To je končni – minimalni – model linearne regresije za modeliranje FTW s parametri BPD, FL, CP in AP in njenimi višjimi členi.
Ko enkrat imamo definiran minimalni model, lahko izvedemo modeliranje z multiplo linearno regresijo v Jamovi, tako kot pri vaji iz pog. 6.3 le da za opisni spremenljivki izberemo BPDAP in FL2.
6.6 Logistična regresija
Postopek reševanja
V Excel datoteki titanic3.xlsx imamo zbrane podatke o potnikih Titanika. Vsaka vrstica v Excelu predstavlja enega potnika. Zanimajo nas naslednje spremenljivke (podatki o potnikih): age (starost), sex (spol), pclass (potovalni razred), parch in sibsp (ali so potovali sami ali z družino). Odpremo podatke v Jamovi program: Open in izberemo željeno datoteko.
Zanima nas, koliko ljudi je preživelo glede na spol in na razred, v katerem so potovali. Spremenljivka survived je kategorijska spremenljivka z dvema kategorijama (0 = oseba je umrla, 1 = oseba je preživela). Spremenljivki sex in pclass sta obe kategorijski spremenljivki. Prva ima dve kategoriji (ženska, moški), druga pa tri (1 = prvi potovalni razred, 2 = drugi potovalni razred, 3 = tretji potovalni razred). Spremenljivke lahko ustrezno popravimo/uredimo pod zavihkom Variables.
Ker ugotavljamo povezave med kategorijskimi spremenljivkami, bomo uporabili kontingenčne tabele. Izvedemo opisno statistiko preživelih in umrlih glede na spremenljivke: sex in pclass.
Analyses -> Frequencies in pod Contingency Tables izberemo Independent Samples χ2 test of assosiation.
Najprej izvedimo analizo za spremenljivko spol. Okno Contingency Tables izpolnimo na prikazani način:
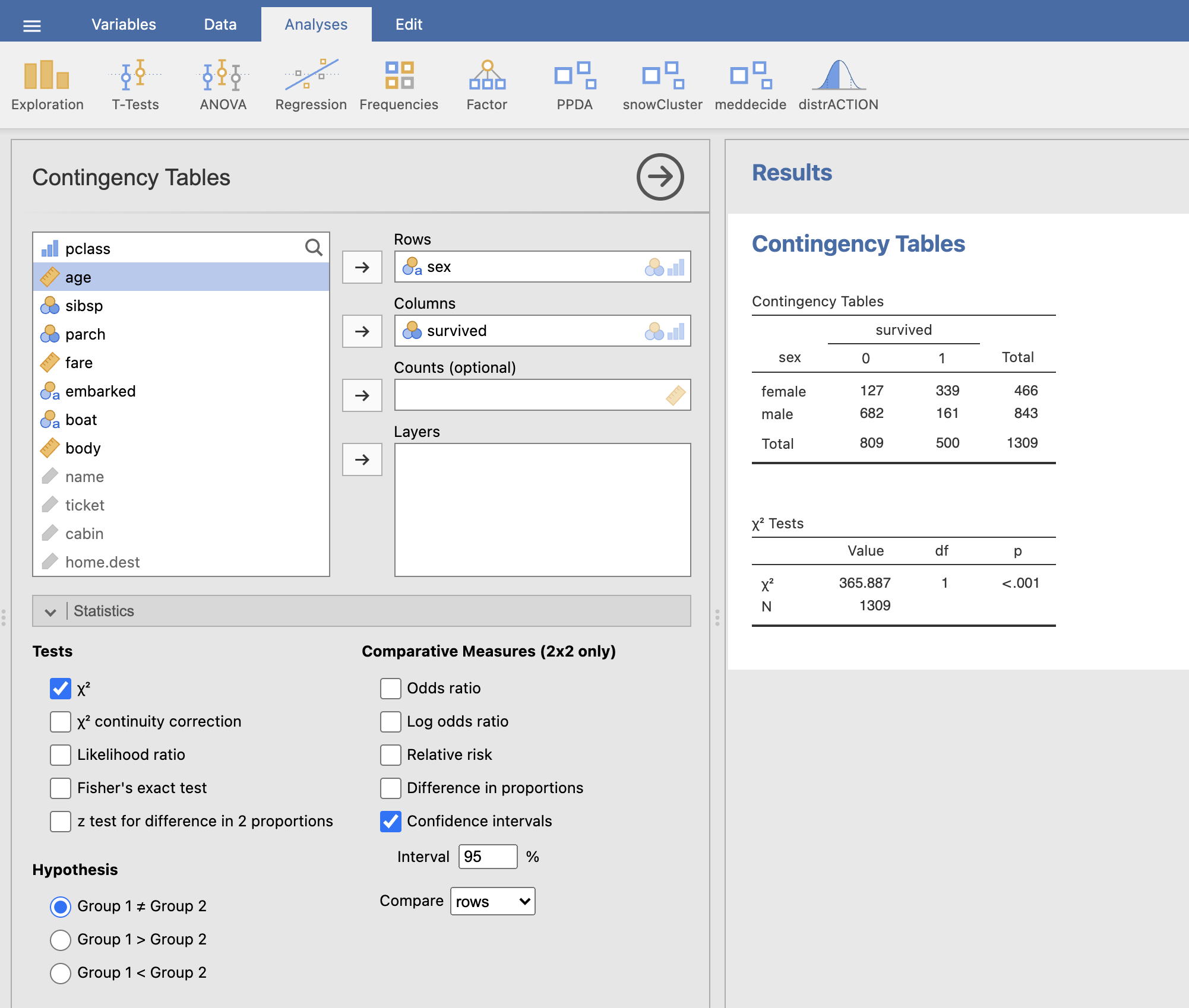
V desnem oknu Results se nam izriše kontingenčna tabela in tabela hi-kvadrat testa. Preživelo je 339 od 466 žensk in 161 od 843 moških. Opazimo, da je preživelo bistveno več potnic ženskega spola. S hi-kvadrat testom preverimo, če je ta razlika statistično značilna. Na podlagi rezultata hi-kvadrat testa ugotovimo, da je razlika v deležih preživelih glede na spol statistično značilna (p < 0.001).
Ponovimo analizo še za spremenljivko, ki govori o potovalnem razredu. Okno Contingency Tables izpolnimo na prikazani način:
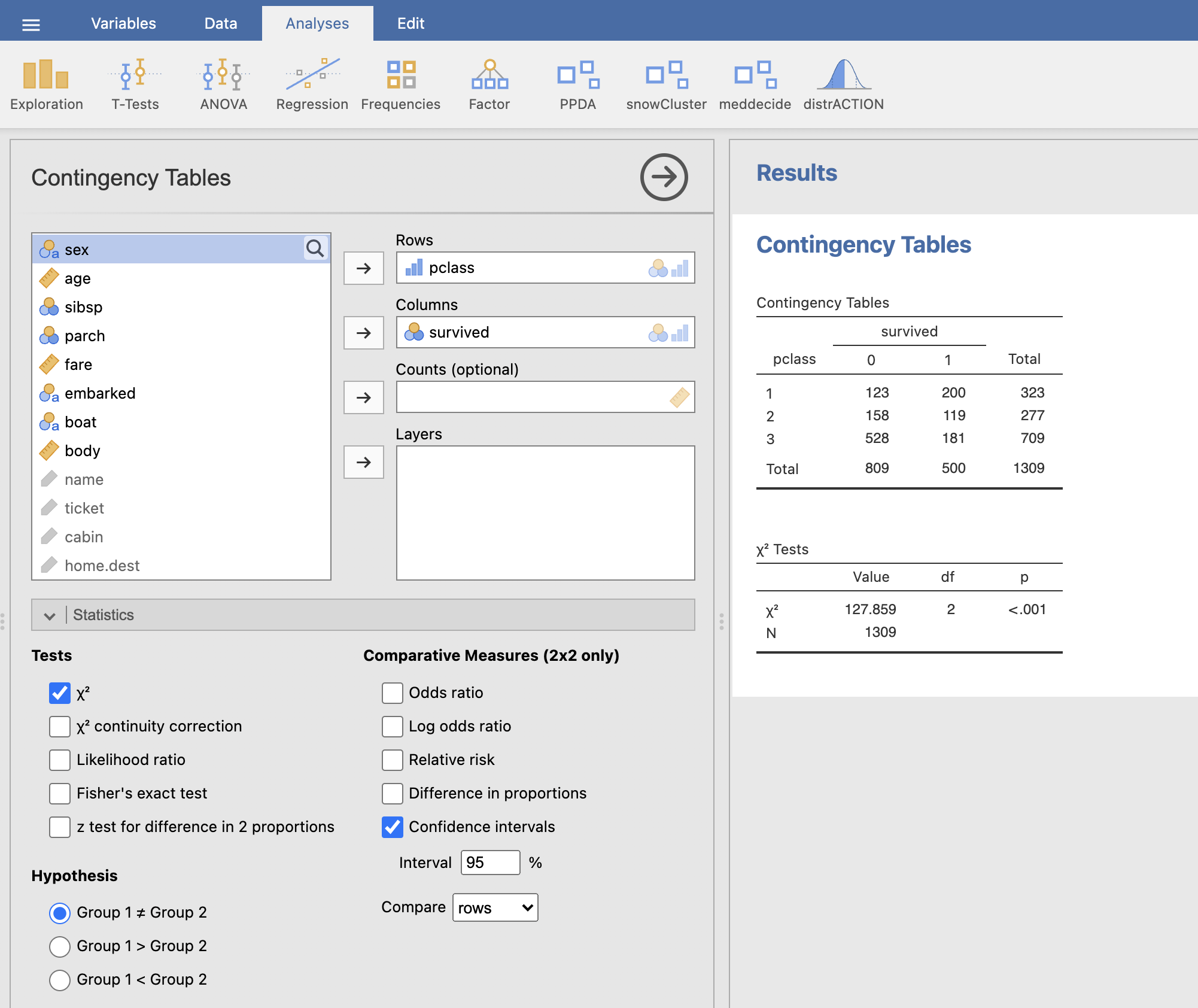
Iz prvega potovalnega razreda je umrlo 123 ljudi od 323, iz drugega potovalnega razreda je umrlo 158 ljudi od 277 in iz tretjega potovalnega razreda je umrlo 528 ljudi od 709. V najnižjem potovalnem razredu jih je umrlo izrazito več kot v najvišjem potovalnem razredu. Na podlagi hi-kvadrat testa ugotovimo, da se deleži za preživelost statistično značilno razlikujejo glede na potovalne razrede (p < 0.001).
Pri spremenljivki starost nas zanima, ali je razlika v povprečni starosti umrlih in preživelih. To testiramo s t-testom za neodvisne spremenljivke. Analyses -> T-Tests -> Independent Samples T-Test.
Testna spremenljivka (Dependent Variables) je age, katero razdelimo glede na kategorijsko spremenljivko (Grouping Variable) survived. Pod možnostjo Additional Statistics izberemo še Descriptives za izpis osnovnih parametrov. V rezultatskem oknu se nam izpišejo rezultati t-testa.
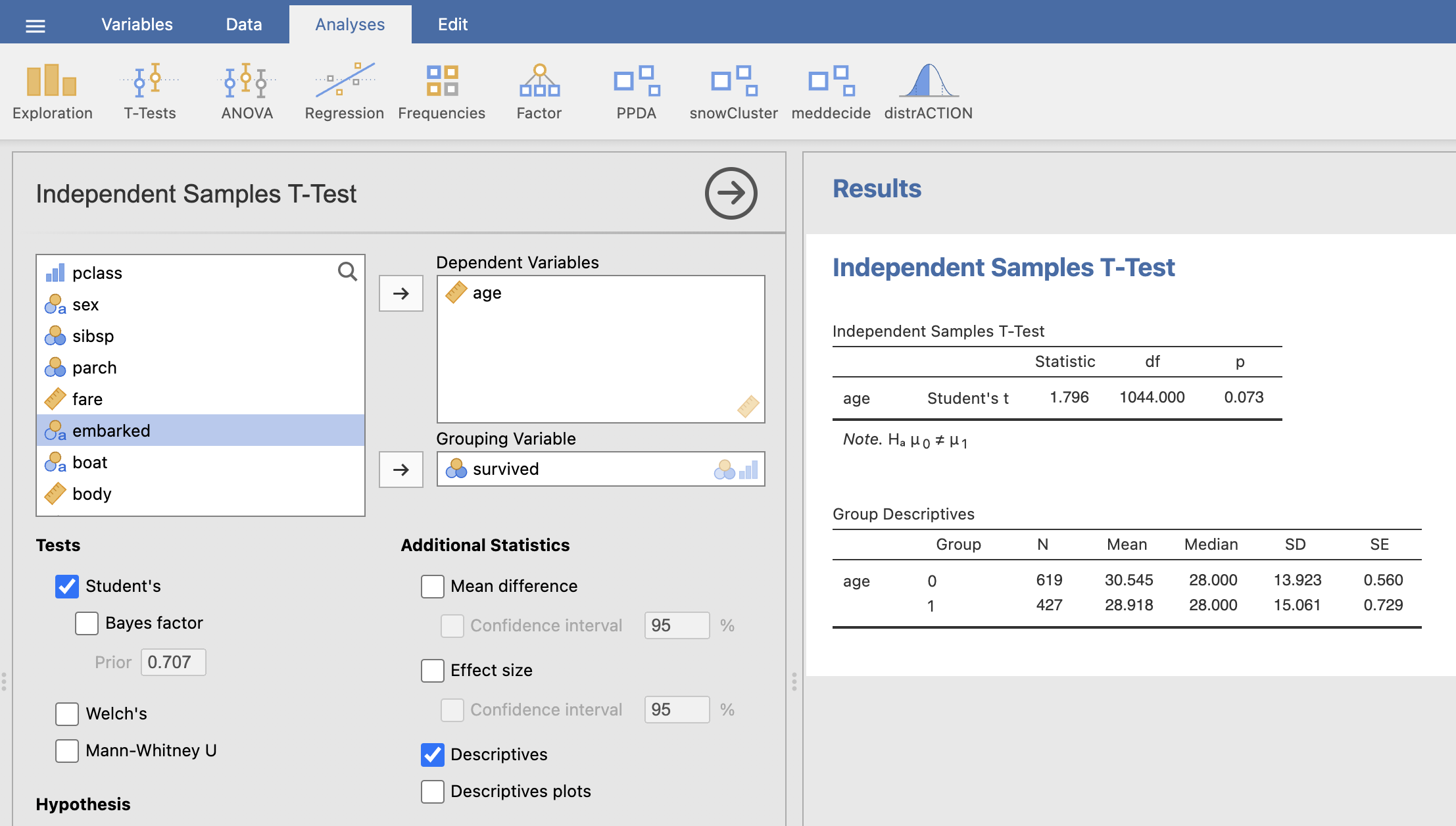
Povprečna starost tistih, ki so umrli je 30.5 let, tistih, ki so preživeli pa 28.9 let. Na prvi pogled opazimo, da bistvene razlike v povprečni starosti med skupinama ni, kar potrdi tudi p-vrednost t-statistike, ki je enaka 0.073. Tako lahko ugotovimo, da ni statistično značilnih razlik v starosti med preživelimi in umrlimi potniki.
Če želimo ugotoviti ali obstaja statistično značilna razlika med potniki, ki so potovali sami in med potniki, ki niso potovali sami moramo v Jamovi programu določiti, katere kategorije spremenljivk sibsp in parch naj program upošteva kot potnike, ki so potovali sami in potnike, ki niso potovali sami.
To naredimo tako, da definiramo novo spremenljivko v zavihku Data z izbiro Compute.
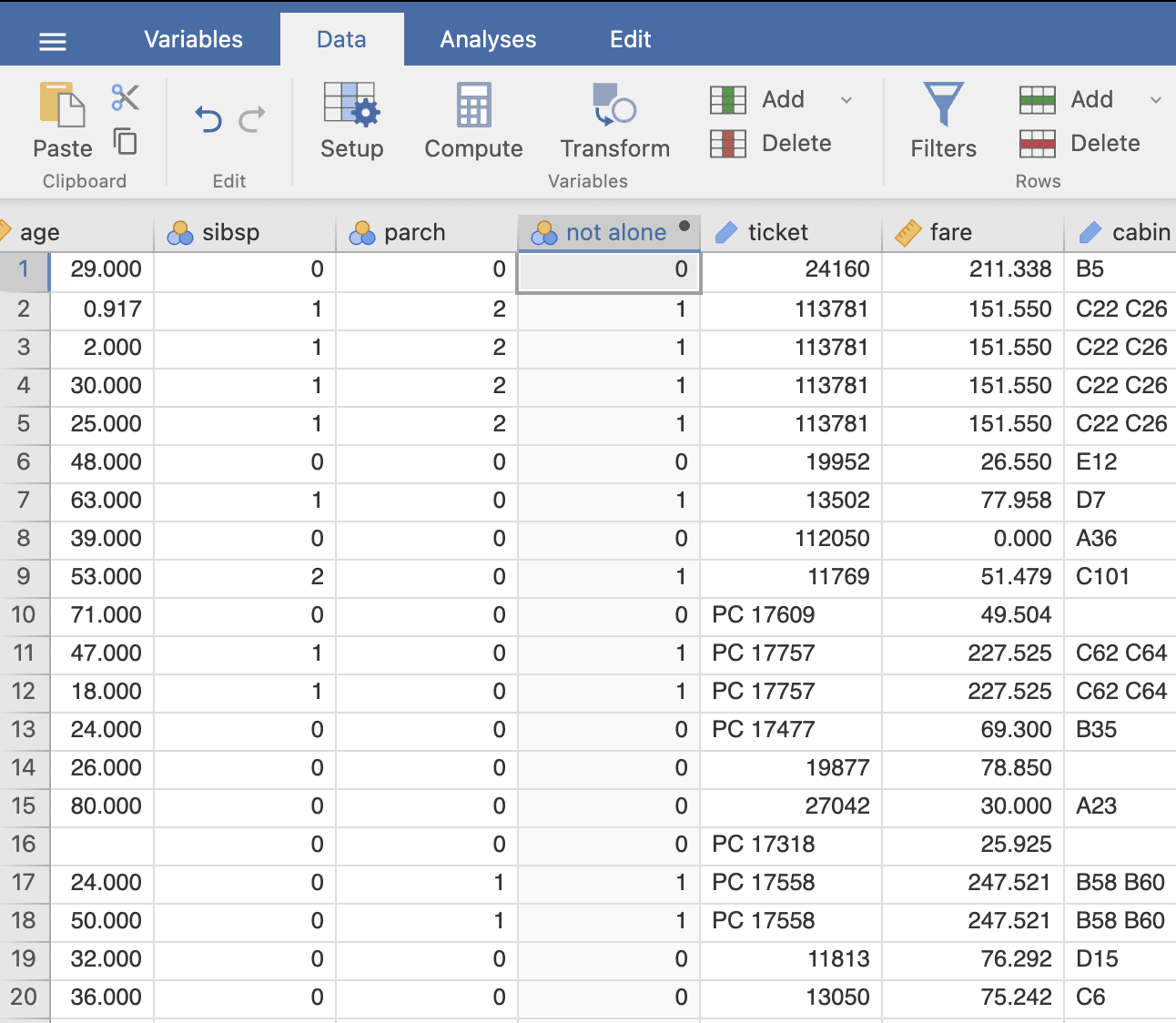
Novo spremenljivko poimenujemo not alone in jo definiramo na naslednji način:
(sibsp > 0) or (parch > 0).
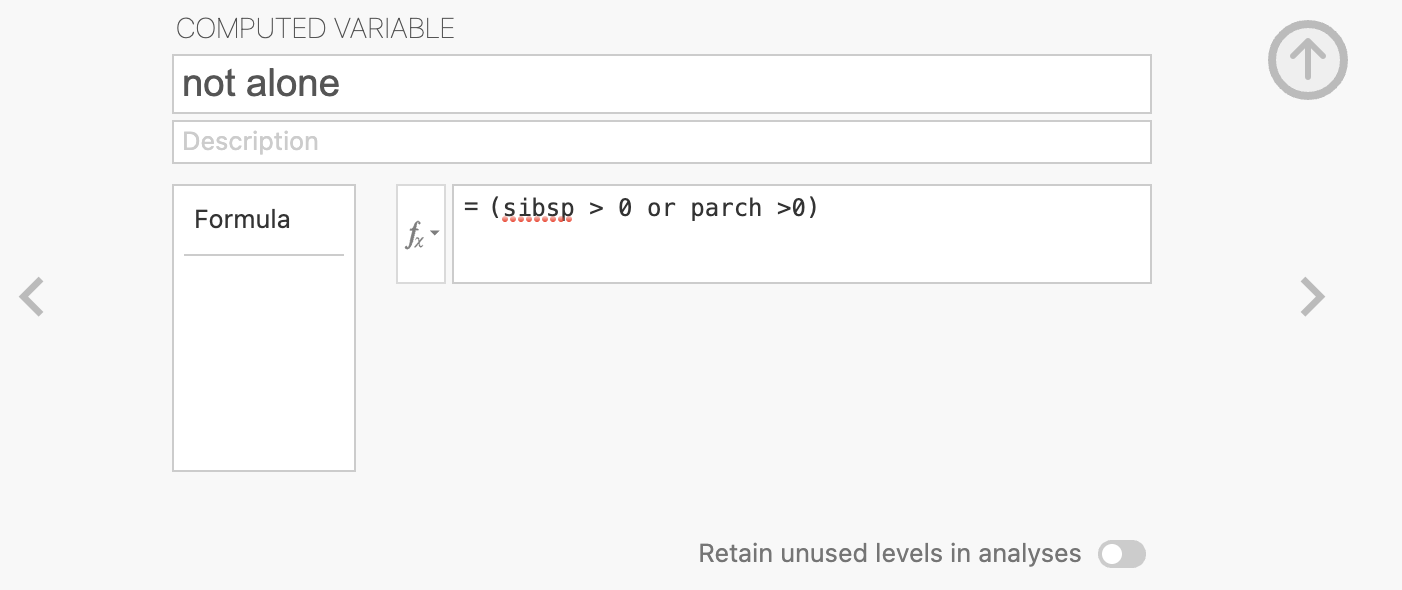
V Data dobimo nov stolpec s spremenljivko not alone, ki je enaka 1 v primeru, če nisi potoval sam in 0, če si potoval sam.
Nato izrišemo kontingenčno tabelo in izvedemo hi-kvadrat test. Analyses -> Frequencies in pod Contingency Tables izberemo Independent Samples χ2 test of assosiation.
Okno Contingency Tables izpolnimo na prikazani način:
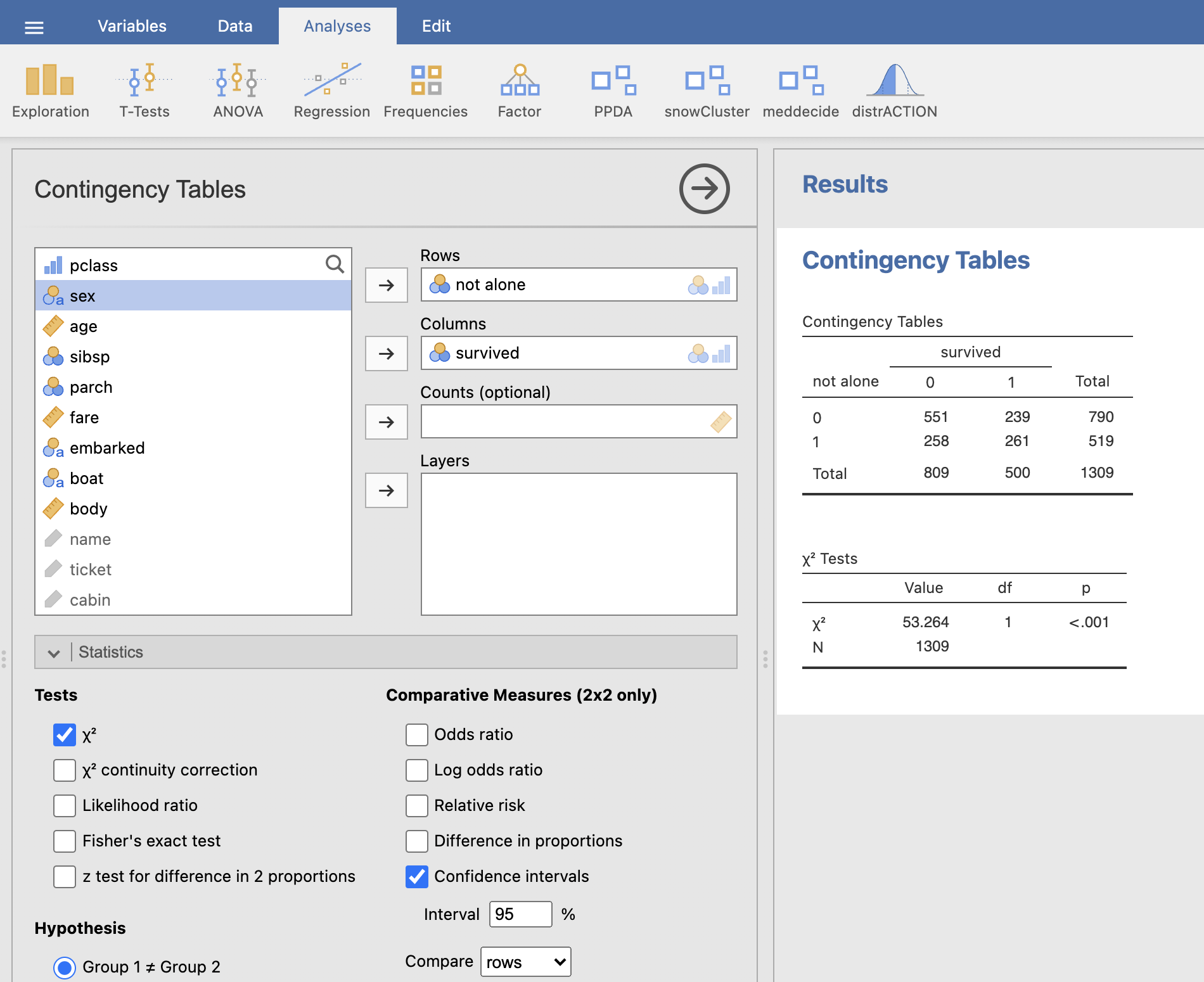
V oknu Results se nam izriše kontingenčna tabela in tabela hi-kvadrat testa. Na podlagi rezultatov ugotovimo, da obstajajo statistično značilne razlike med preživelimi in umrlimi glede na to ali so potovali sami ali ne (p < 0.001).
Izvedimo model multiple logistične regresije, kjer bomo modelirali razmerje obetov za preživetje posameznika glede na njegovo starost, spol, razred potovanja in ali je potoval sam ali ne. To izvedemo z ukazom Analyses -> Regression in pod Logistic Regression izberemo 2 Outcomes Binomial.
Kot odzivno spremenljivko izberemo survived, kot opisne spremenljivke pa izberemo pclass, sex, age, not alone. Skalarne opisne spremenljivke (age) vstavimo v Covariates, kategorijske opisne spremenljivke pa v Factors. Pri kategorijskih spremenljivkah se računa razmerje obetov glede na referenčno kategorijo. Ob določitvi kategorijskih spremenljivk v razdelku Reference Levels določimo, da bo referenčna kategorija pri opisnih kategorijskih spremenljivkah zadnja.
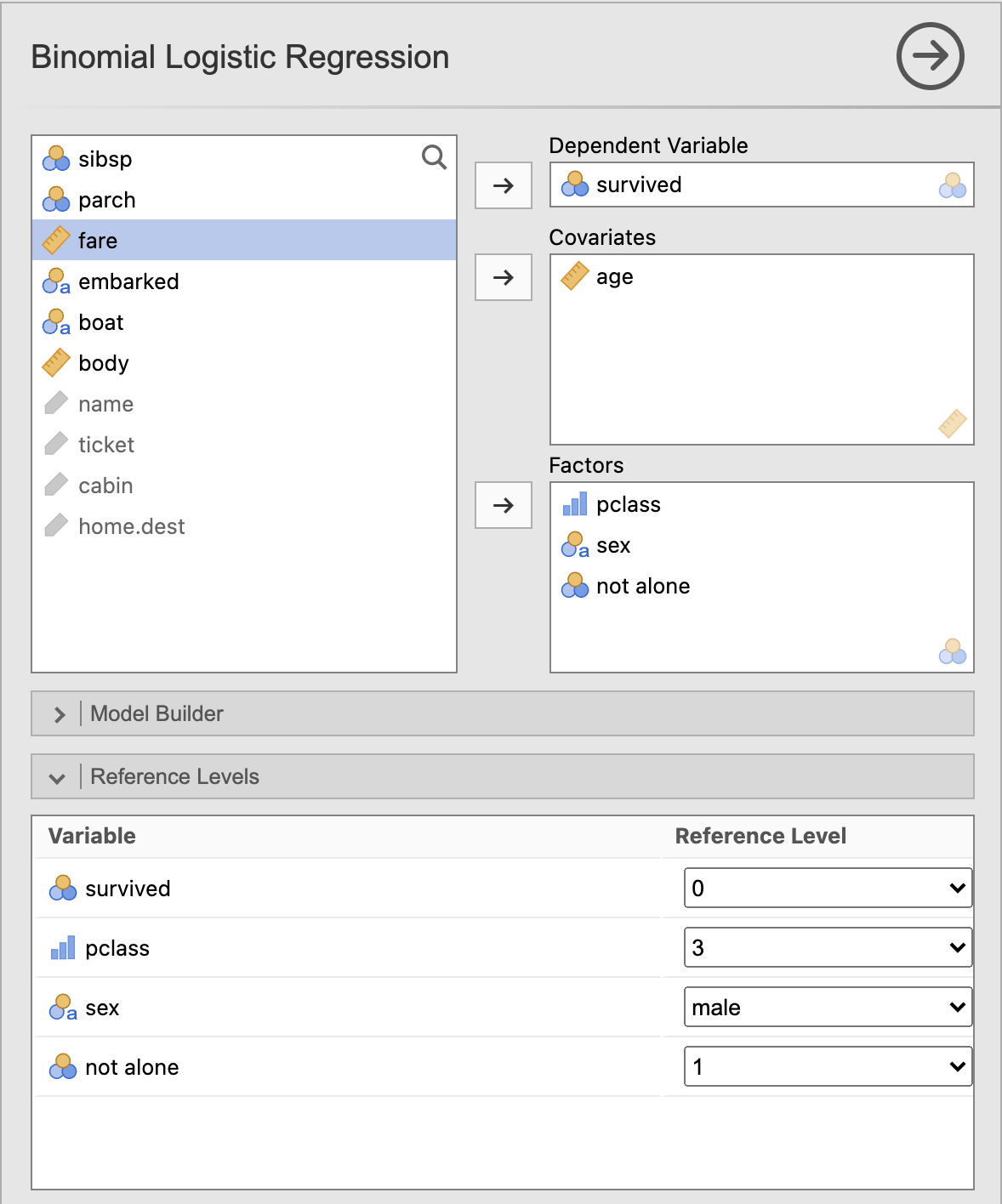
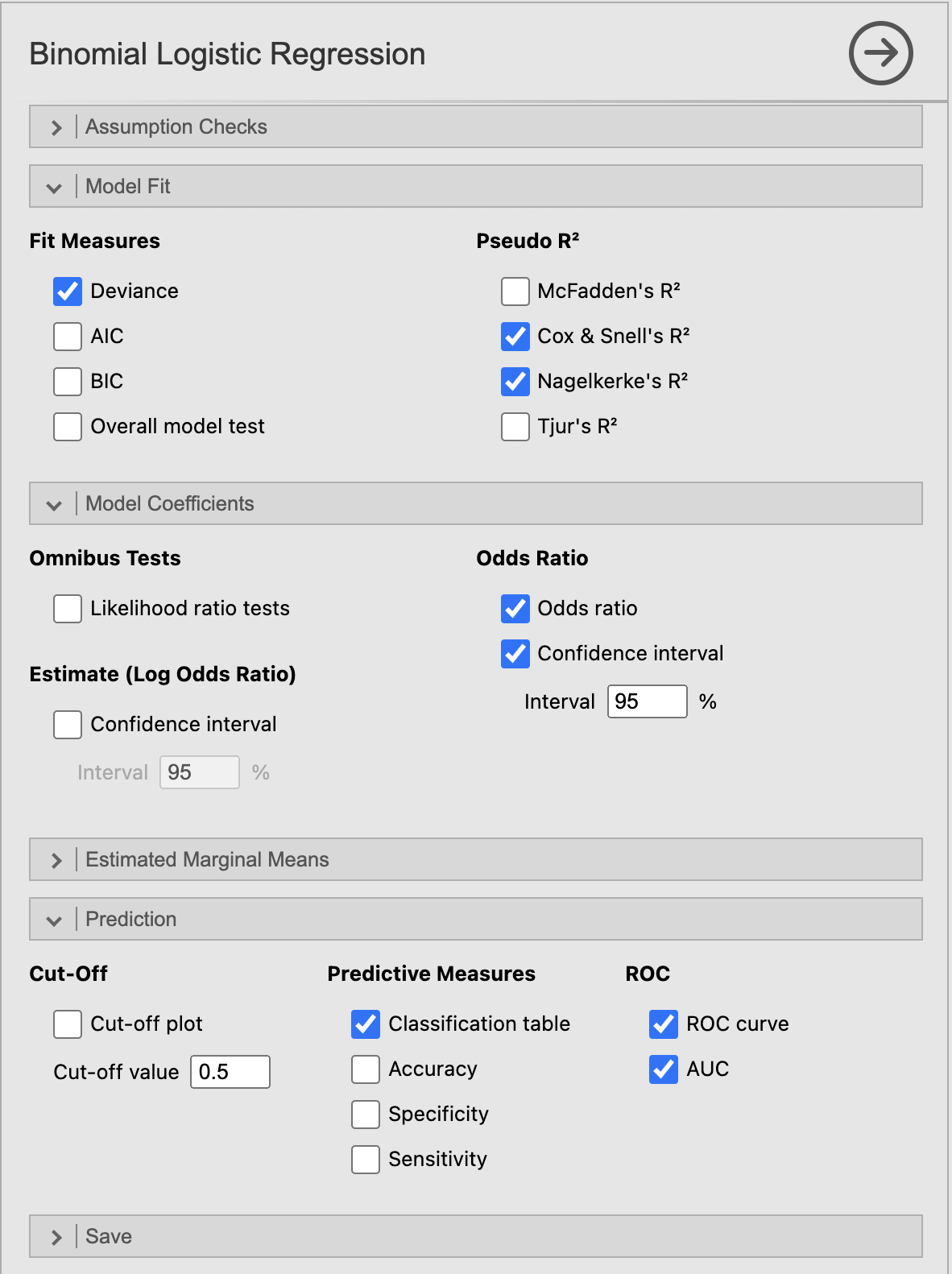
Pod razdelkom Model FIt pri Fit Measures označimo Deviance, pri Pseudo R2 pa Cox & Snell’s R2 in Nagelkerke’s R2 za izračun kakovosti logističnega modela.
Pod razdelkom Model Coefficients pri Odds Ratio označimo Odds ratio za izpis razmerja obetov in Confidence interval: 95 % za izpis intervalov zaupanja v ocene regresijskih parametrov.
Za preverjanje ustreznosti in učinkovitosti modela pod razdelkom Prediction pri Predictive Measures označimo Classification table in pri ROC izris ROC krivulje (ROC curve) in izračun AUC (AUC).
V desnem oknu Results dobimo rezultate željenih analiz.
V tabeli Model Coefficients - survived nas zanimajo predznaki regresijskih koeficientov (stolpec Estimate), statistična značilnost (stolpec p) in razmerje obetov (stolpec Odds ratio). Če je vrednost regresijskih koeficientov pozitivna pomeni, da se razmerje obetov za preživetje povečuje, če pa je negativna pa se razmerje obetov preživetja zmanjšuje. Statistična značilnost nam pove ali je regresijski koeficient od nič statistično značilno različen. Ugotovimo, da so statistično ustrezni parametri pclass, sex in age, parameter not alone pa ni statistično značilno od nič različen (p = 0.778), kar pomeni, da to, ali je nekdo potoval sam ali ne, ni statistično pomemben dejavnik za preživetje. Na podlagi vrednosti razmerja obetov v tabeli ugotovimo naslednje:
Potniki prvega razreda so imeli 9.757-krat večjo verjetnost preživetja kot potniki tretjega razreda (referenčna kategorija je zadnja kategorija, torej potniki tretjega razreda). Potniki drugega razreda so imeli 2.733-krat večjo verjetnost, da so preživeli kot potniki tretjega razreda. Ker noben od intervalov zaupanja ne vsebuje 1.0, sta ta razmerja obetov statistično značilna.
Pri spremenljivki spol, ugotovimo, da so imele ženske 12-krat večjo verjetnost preživetja kot moški (moški so referenčna kategorija).
Pri spremenljivki starost nam vrednost 0.967 pove, da se možnost preživetja zmanjša za 0.967-krat z vsakim letom starosti. Interval ne vsebuje 1.0, kar pomeni, da je to statistično značilno zmanjšanje.
Kakovost logističnega modela predstavljata naslednji tabeli:
Podatki v tabeli Model Fit Measures govorijo o izračunanem determinacijskem koeficientu, ki po prvem izračunu znaša 0.338, po drugem pa 0.457. Tako lahko zaključimo, da je determinacijski koeficient modela med 0.338 in 0.457, oziroma da z modelom opišemo med 33.8 % in 45.7 % variance preživelih.
Učinkovitost modela za pravilno napovedovanje preživetja na podlagi modeliranih spremenljivk preberemo iz spodnje tabele:
Tabela Classification Table predstavlja kontingenčno tabelo napovedovanja preživetja, če za mejno vrednost verjetnosti preživetja pri logističnem modelu izberemo verjetnost 0.5. Verjetnost modela nad 0.5 pomeni preživetje, verjetnost pod 0.5 pa ne. V tem primeru pravilno napovemo 518 umrlih in 304 preživele, s skupno točnostjo 78.6 %.
Ustreznost modela za napovedovanje preživelih pa lahko preverimo tudi z ROC analizo.
Ugotovimo, da je AUC za napovedovanje preživelih z modelom logistične regresije iz spremenljivk starosti, spola in potovalnega razreda enaka 0.840, kar je dobro.