4 Intervali zaupanja v oceno statistik
4.1 Intervali zaupanja v oceno povprečja
V datoteki kreatinin_akin.sav so podatki o pacientih, ki so imeli operacijo na srcu (Kališnik et al. 2017). Merili smo jim različne podatke, pacienti pa so ločeni glede na okvaro delovanja funkcije ledvic v dve skupini.
- Za vsako skupino določi intervale zaupanja v oceno povprečja in komentiraj, ali lahko samo na podlagi teh intervalov, kaj rečemo o skupinah brez in z okvaro delovanja funkcije ledvic.
V programu Jamovi odpremo podatke iz naloge: Open in najdemo ustrezno datoteko kreatinin_akin.sav.
Podatki so organizirani tako, kot je prikazano na spodnji sliki:
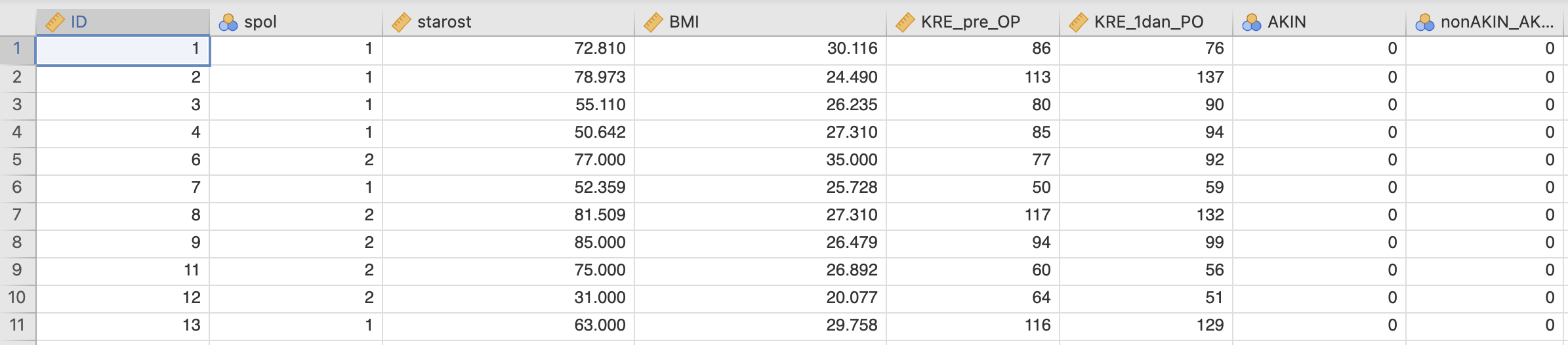
Pacienti, ki so imeli okvaro delovanja ledvic so v skupini nonAKIN_AKIN = 1, brez okvare pa nonAKIN_AKIN = 0. Skupaj imamo 263 pacientov.
Skalarnim spremenljivkam izračunamo povprečje in interval zaupanja v povprečje posebej za tiste, ki imajo okvaro ledvic (nonAKIN_AKIN = 1) in za tiste, ki okvare ledvic nimajo (nonAKIN_AKIN = 0). Zanimajo nas spremenljivke: starost, BMI, kreatinin pred operacijo in kreatinin po operaciji.
Željene vrednosti izračunamo z ukazom: Analyses -> Exploration -> Descriptives, kjer pod Variables izberemo spremenljivke: starost, BMI, KRE_pred, KRE_po glede na faktor (Split by): nonAKIN_AKIN. Pod razdelkom Statistics označimo Mean pri Central Tendency in Confidence interval for Mean pod Mean Dispersion. Interval zaupanja v oceno povprečja je 95 %.
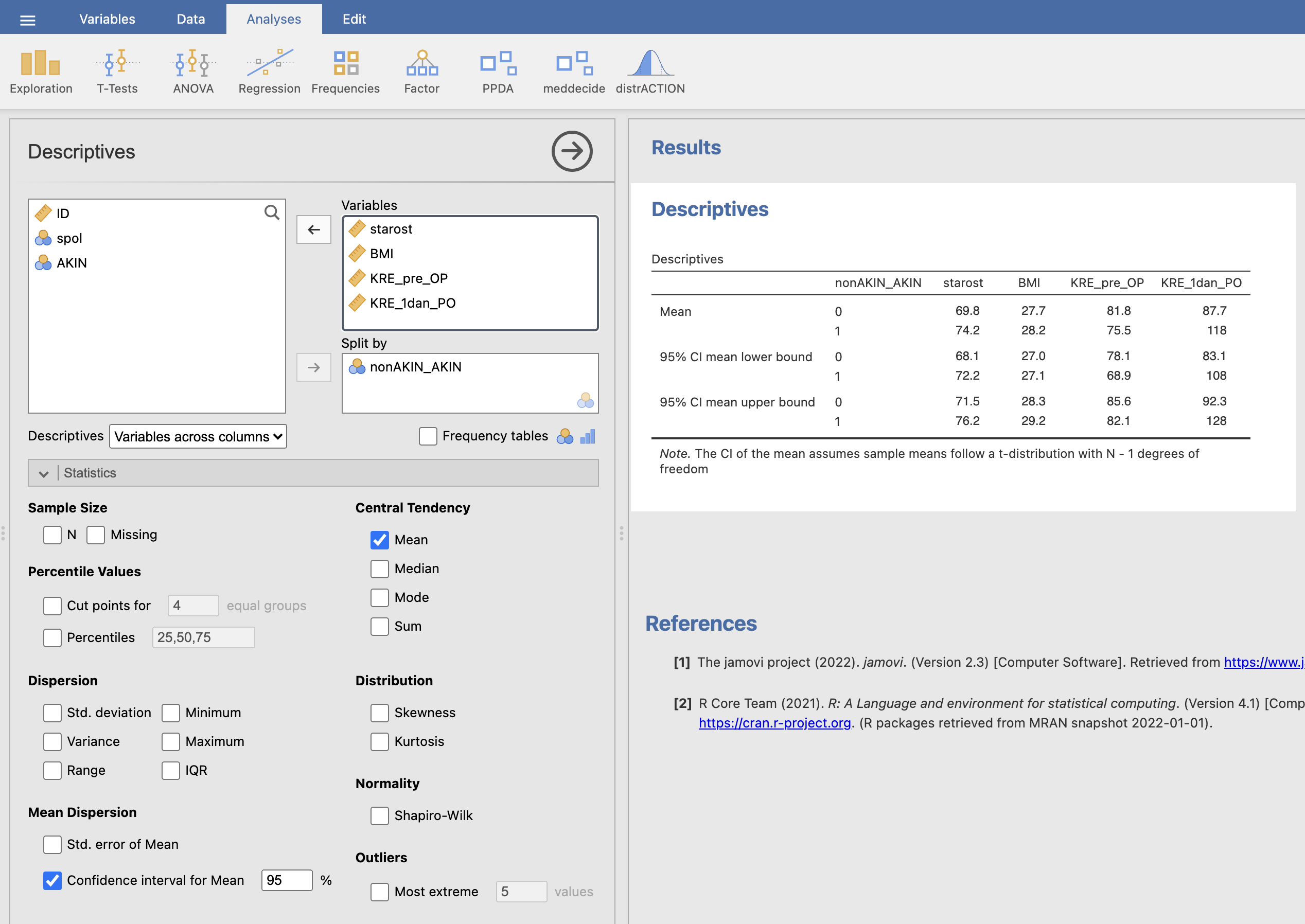
V desnem oknu Results dobimo tabelo, ki vsebuje povprečja in meje 95 % intervala zaupanja v povprečje za izbrane spremenljivke. Statistike so deljene posebej za paciente brez okvare ledvic (nonAKIN_AKIN = 0) in za paciente z okvaro ledvic (nonAKIN_AKIN = 1).
Iz dobljenih rezultatov naredimo tabelo in za vsako izmed spremenljivk izpišemo potrebne podatke (povprečje [95 % interval zaupanja]):
| AKIN NE povp. [95 % CI] |
AKIN DA povp. [95 % CI] |
|
|---|---|---|
| starost | 69.8 [68.1, 71.5] | 74.2 [72.2, 76.2] |
| BMI | 27.7 [27.0, 28.3] | 28.2 [27.1, 29.2] |
| kreatinin pred operacijo | 81.8 [78.1, 85.6] | 75.5 [68.9, 82.1] |
| kreatinin po operaciji | 87.7 [83.1, 92.3] | 118.0 [108.0, 128.0] |
Iz tabele lahko razberemo, da se povprečna starost med skupinama razlikuje. Ker se intervala zaupanja v oceno povprečja ne prekrivata, lahko trdimo, da je razlika med povprečjema starosti statistično značilna.
Na podoben način komentiramo tudi razlike med opazovanima skupinama pri ostalih spremenljivkah:
V povprečju je BMI pri bolnih višji, ampak ne moremo trditi, da je ta razlika statistično značilna, saj se intervala zaupanja prekrivata.
Kreatinin, izmerjen pred operacijo, je višji pri zdravih, vendar pa ker se intervala zaupanja prekrivata, ne moremo trditi, da je razlika statistično značilna.
Kreatinin, izmerjen po operaciji, je občutno nižji pri bolnikih, ki okvare ledvic nimajo v primerjavi z bolniki, ki imajo okvaro ledvic. Ta razlika je statistično značilna, saj se intervala zaupanja ne prekrivata.
Interval zaupanja v povprečje je interval, za katerega lahko s 95 % verjetnostjo trdimo, da se populacijsko povprečje nahaja znotraj tega intervala.
Če primerjamo dva intervala zaupanja v povprečje lahko ugotovimo, ali obstajajo statistično značilne razlike med dvema povprečjema. V primeru prekrivanja intervalov statistično značilnih razlik ni, če pa se intervala ne prekrivata, obstajajo statistično značilne razlike med povprečjema.
Tako ugotovimo, da so bolniki z okvaro ledvic v povprečju statistično značilno starejši in imajo višje vrednosti kreatinina po operaciji kot bolniki brez okvare ledvic.
4.2 Intervali zaupanja v epidemiološki statistiki
Pri vaji v pog. 2.3 smo računali relativno tveganje in razmerje obetov pri presečni študiji.
- Izračunaj še intervale zaupanja v oceno RR in OR in komentiraj rezultate.
Ponovimo postopek vaje iz pog. 2.3, kjer smo pripravili podatke za statistično analizo.
Ko smo pripravili podatke za obdelavo, izvedemo statistično analizo z izvedbo ukaza Analyses -> Frequencies in pod Contingency Tables izberemo Independent Samples χ2 test of assosiation.
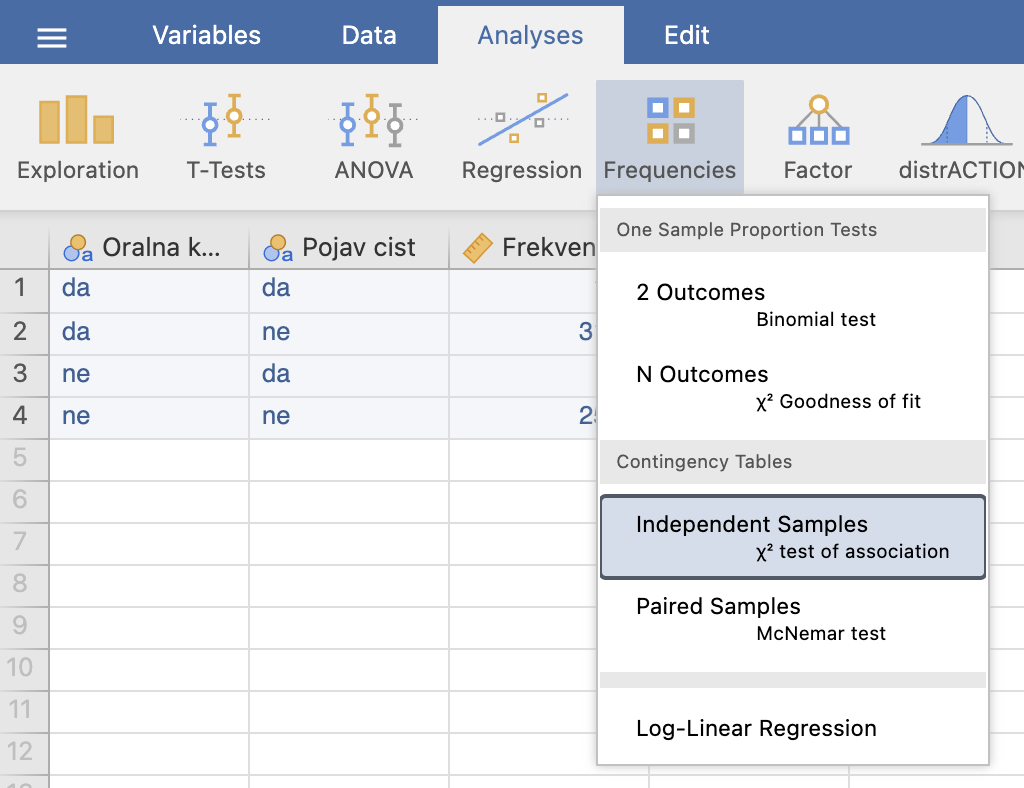
V levem oknu Contingency Tables izberemo, katera kategorijska spremenljivka bo izpisana v vrsticah (Rows = Oralna kontracepcija) in v stolpcih (Columns = Pojav cist) kontingenčne tabele. Pod možnost Counts (optional) dodamo spremenljivko Frekvenca. S tem posamezne kombinacije meritev obtežimo s števili zapisanimi v spremenljivki Frekvenca.
Za izračun relativnega tveganja v razdelku Statistics označimo Relative risk, za izračun razmerja obetov pa Odds ratio. Prav tako označimo Confidence intervals za izpis intervala zaupanja v RR in OR, ki je enak 95 %.
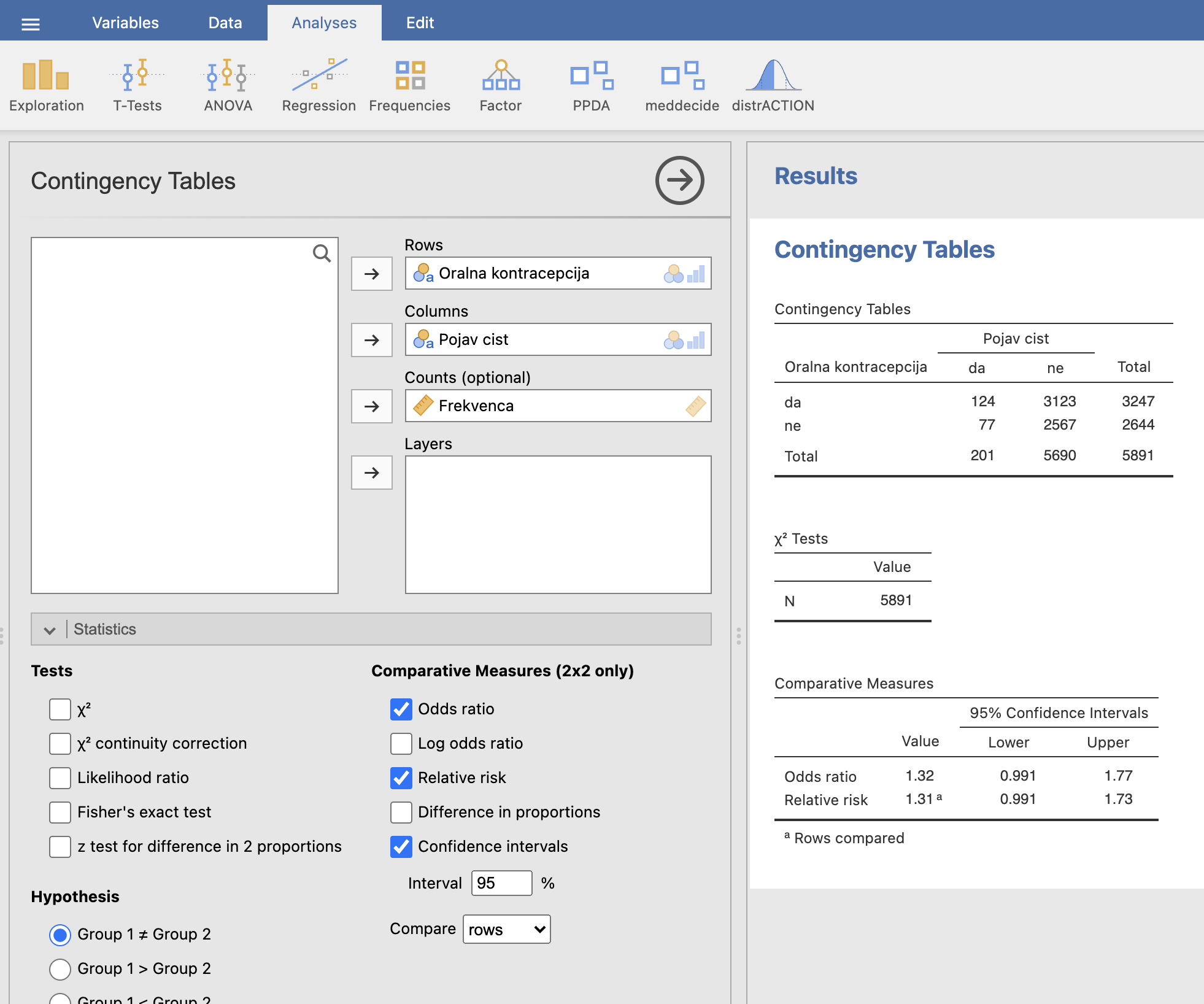
V desnem oknu Results se izpiše tabela izračuna tveganj Comparative Measures s pripadajočimi intervali zaupanja.
Razmerje obetov je OR = 1.32, relativno tveganje pa RR = 1.31. 95 % interval zaupanja za OR je med 0.991 in 1.77, za RR pa med 0.991 in 1.73.
Z izračunom tveganja v Jamovi smo izvedli analizo presečne študije, kjer analiziramo uporabo oralne kontracepcije in pojav cist na dojkah.
Razmerje obetov OR je 1.32, kar pomeni, da je v skupini preiskovank s cistami na dojkah za 1.32-krat večji delež preiskovank, ki uporabljajo oralno kontracepcijo. 95 % interval zaupanja razmerja obetov OR je med 0.991 in 1.767. V intervalu zaupanja se nahaja vrednost 1, kar pomeni, da v skupini preiskovank ni statistično večjega deleža preiskovank z uporabo oralne kontracepcije. Vrednost intervala zaupanja je zelo pomembna, saj se na podlagi tega odločimo o statistični značilnosti OR. Zato se vrednosti OR vedno zapisujejo kot OR [95 % CI]. V našem primeru to pomeni: OR = 1.32 [0.991, 1.77]
Podobno lahko zaključimo tudi, če zapišemo RR v obliki RR [95 %CI]. V našem primeru je RR = 1.31 [0.991, 1.73], kar pomeni, da oralna kontracepcija ne predstavlja statistično značilnega tveganja za pojav cist.