3  Osnovne statistike v diagnostiki

3.1 Senzitivnost, specifičnost, točnost

Navodila vaje

V datoteki diag_sistemi.xlsx imamo podatke o dveh diagnostičnih metodah, s katerima diagnosticiramo neko bolezen:

1. če bolezen diagnosticiramo, označimo s P,
2. če bolezni ne diagnosticiramo, označimo z N.

Postopka primerjajmo z dejansko diagnozo:

1. izračunaj specifičnost in senzitivnost obeh postopkov,
2. izračunaj še točnost diagnostičnih postopkov,
3. podaj ustrezne zaključke.

Postopek reševanja

Odpremo podatke, zapisane v Excel datoteki, s programom Jamovi. Open -> diag_sistemi.xlsx.

Podatki so shranjeni v treh spremenljivkah diag sistem 1, diag sistem 2 in dejanska diagnoza.

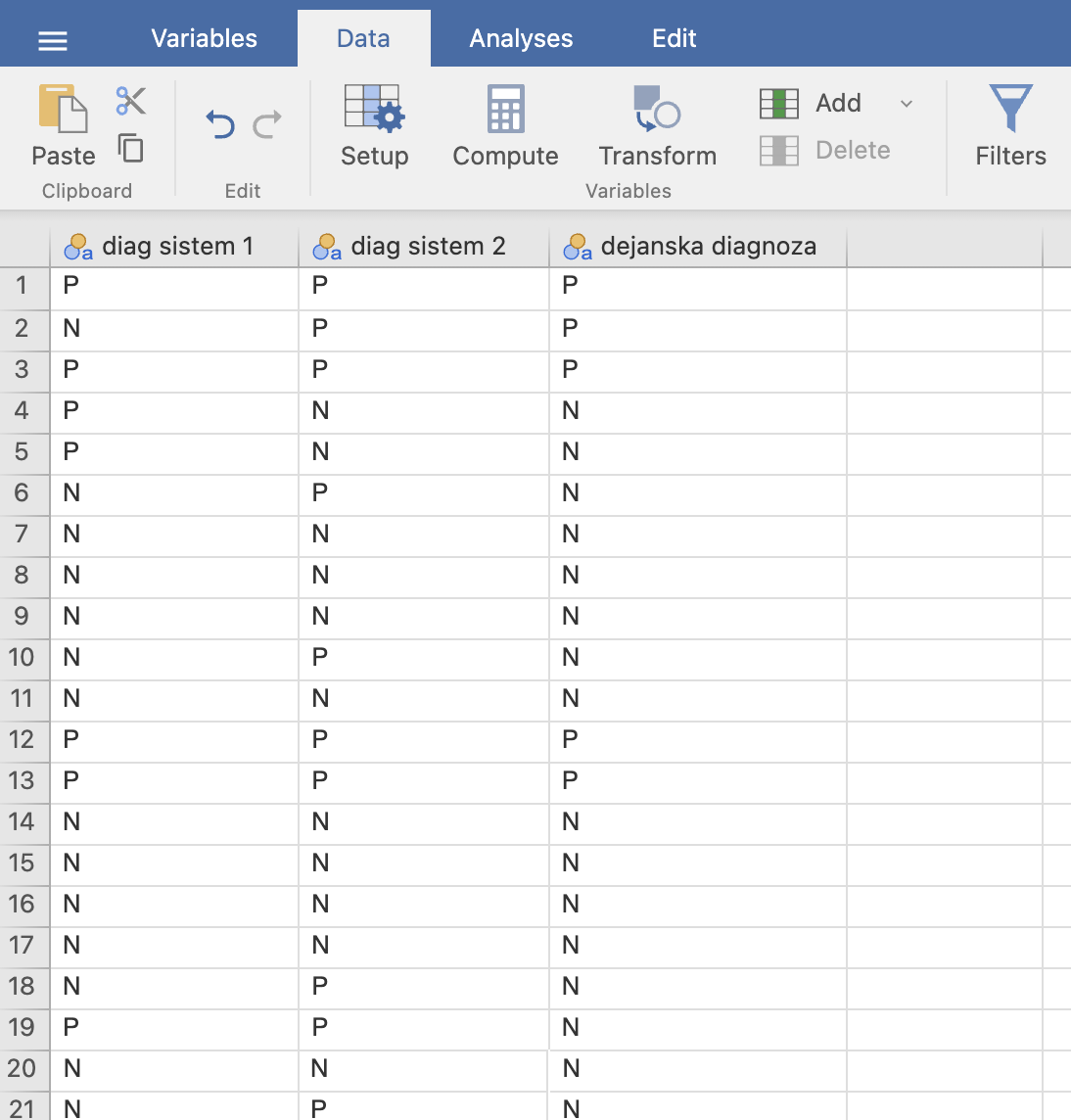
Spremenljivka diag sistem 1 predstavlja testno diagnozo prvega diagnostičnega sistema, spremenljivka diag sistem 2 predstavlja testno diagnozo drugega diagnostičnega sistema, spremenljivka dejanska diagnoza pa dejansko referenčno diagnozo, s katero bomo primerjali oba testna diagnostična sistema. Število primerjav je 51.

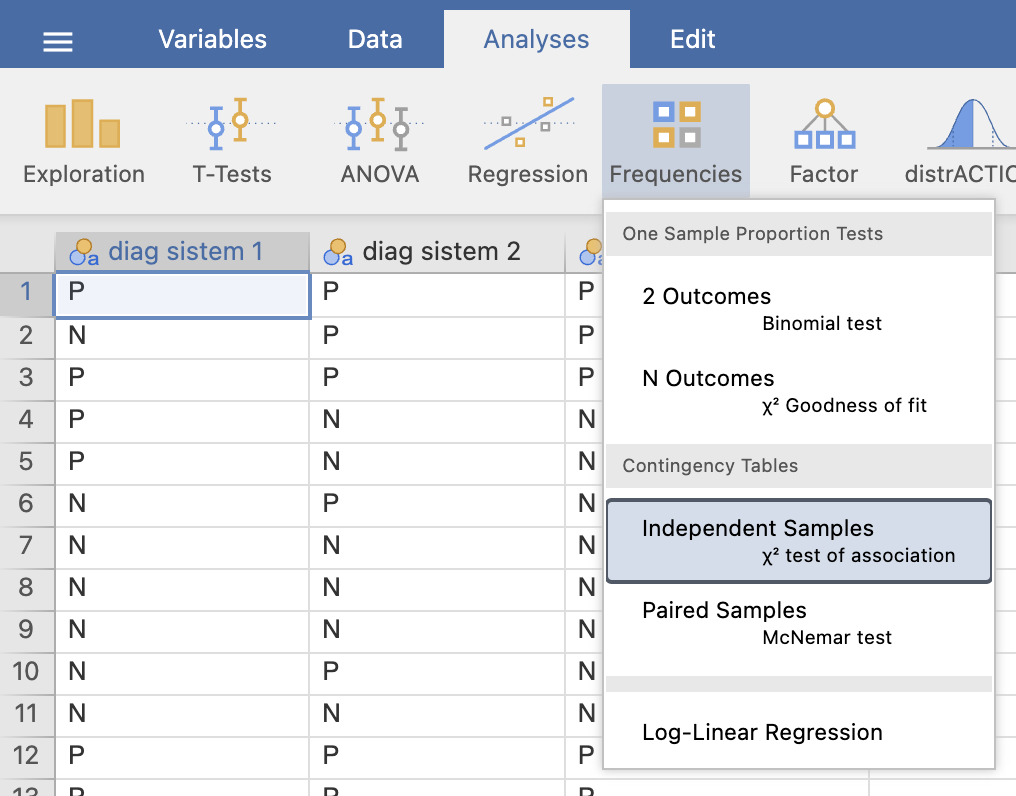
Specifičnost in senzitivnost izračunamo z Analyses -> Frequencies in pod Contingency Tables izberemo Independent Samples χ2 test of assosiation.

V levem oknu izberemo, da bo spremenljivka diag sistem 1 v kontingenčni tabeli zapisana v vrsticah (Rows), dejanska diagnoza pa v stolpcih (Columns). Da bi izračunali senzitivnost in specifičnost diagnostičnega sistema 1, pod razdelkom Cells označimo Observed counts in Column. S tem bomo izpisali odstotke po stolpcih.

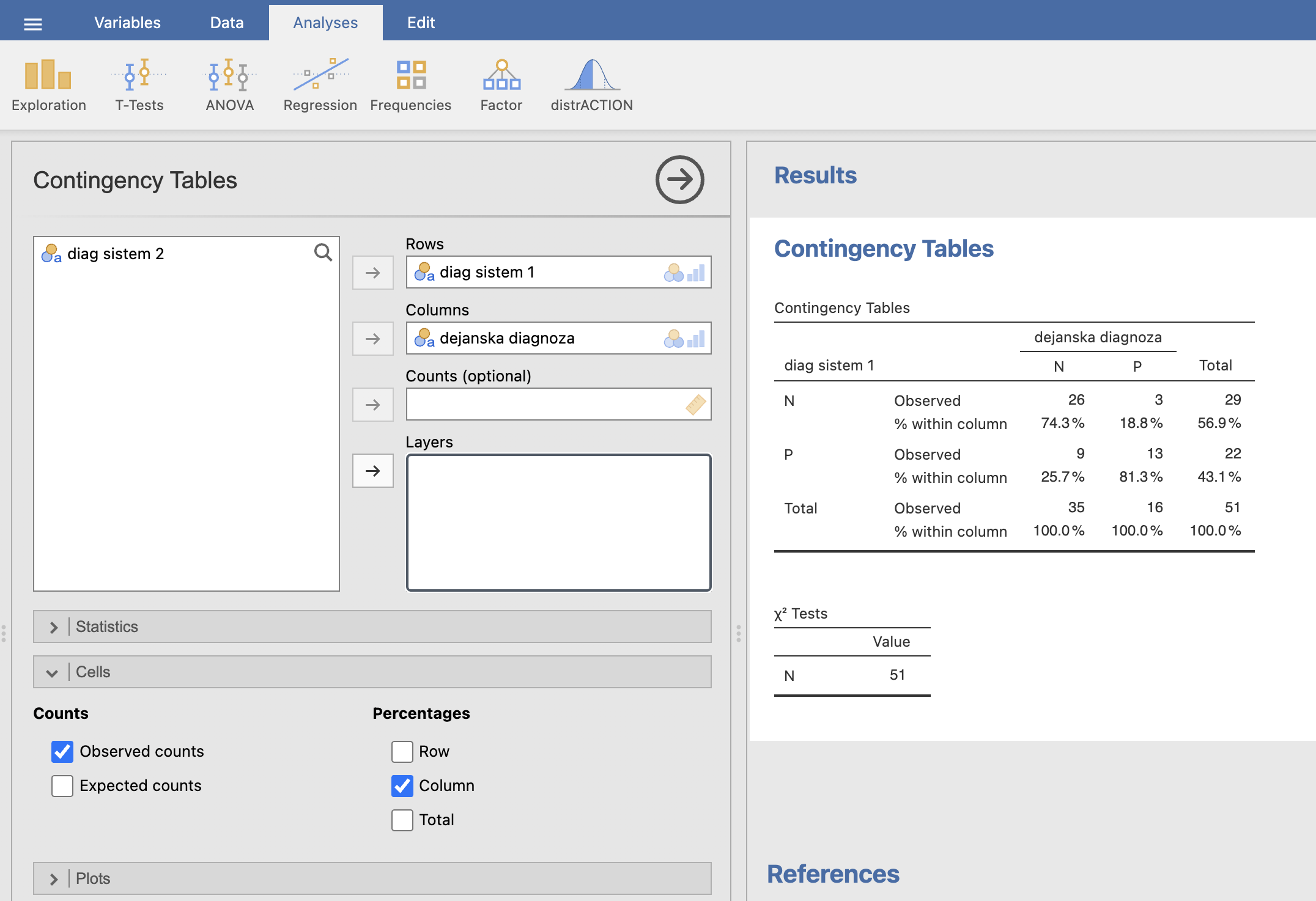
V desnem oknu Results dobimo izpisano kontingenčno tabelo s pripadajočimi odstotki, iz katere lahko preberemo senzitivnost in specifičnost.

Senzitivnost preberemo iz odstotka celice s pozitivno dejansko diagnozo in pozitivno diagnozo prvega diagnostičnega sistema, torej \(senzitivnost = 81.3\) %. Senzitivnost predstavlja delež, kako dobro testni diagnostični sistem napove pozitivno diagnozo (bolezen) glede na referenčno diagnozo.

Specifičnost preberemo iz odstotka celice z negativno dejansko in negativno testno diagnozo, kar v našem primeru znaša \(specifičnost = 74.3\) %. Specifičnost predstavlja delež pravilno diagnosticiranih negativnih diagnoz (zdravih) v primerjavi z referenčno diagnozo.

Enako ponovimo še za diagnostični sistem 2: Analyses -> Frequencies in pod Contingency Tables izberemo Independent Samples χ2 test of assosiation.

V levem oknu izberemo, da bo spremenljivka diag sistem 2 v kontingenčni tabeli zapisana v vrsticah (Rows), dejanska diagnoza pa v stolpcih (Columns). Da bi izračunali senzitivnost in specifičnost diagnostičnega sistema 2, pod razdelkom Cells označimo Observed counts in Column. S tem bomo izpisali odstotke po stolpcih.

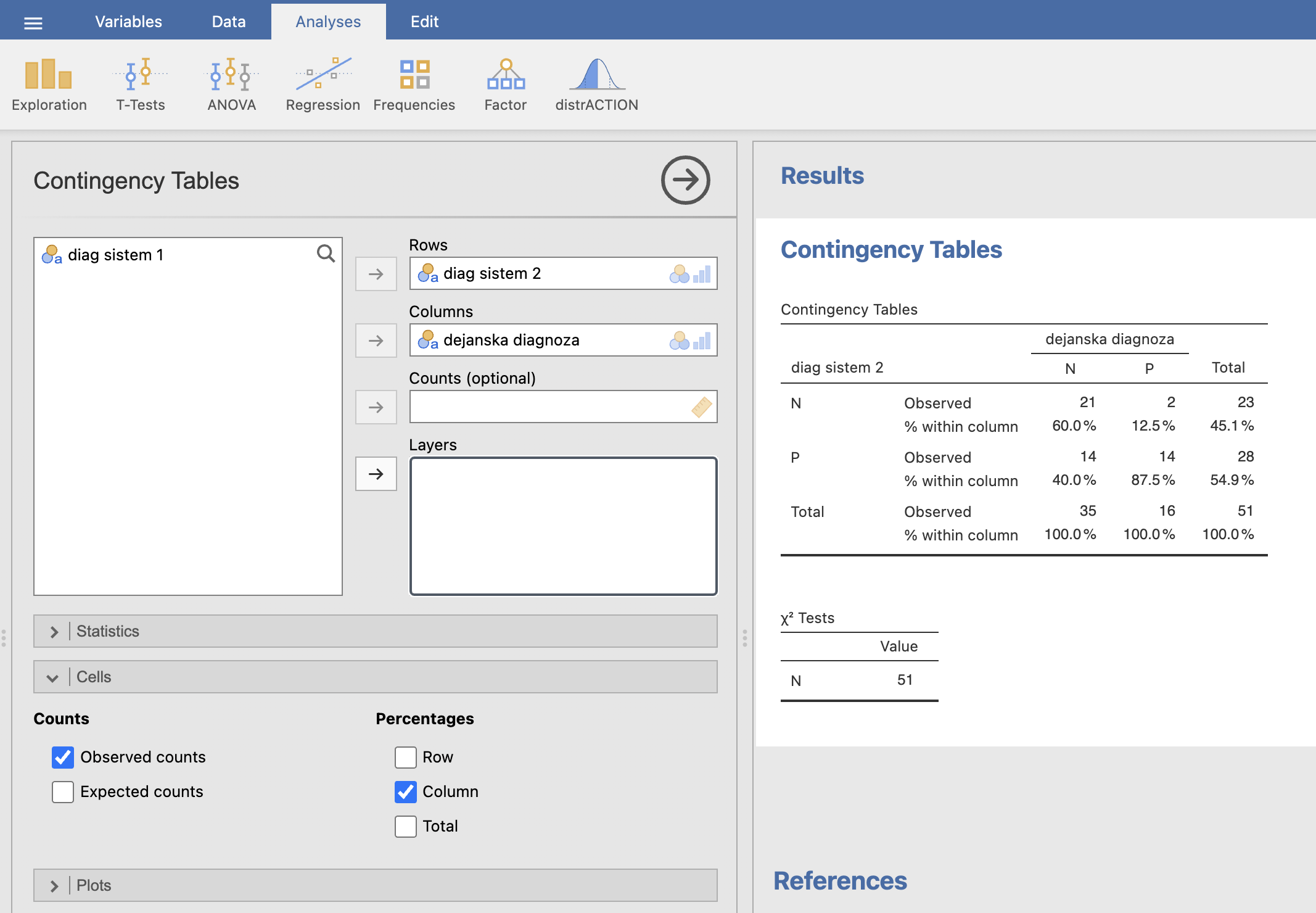
V desnem oknu Results dobimo izpisano kontingenčno tabelo s pripadajočimi odstotki, iz katere lahko preberemo senzitivnost in specifičnost.

\(Senzitivnost\) drugega diagnostičnega sistema je enaka \(87.5\) %, \(specifičnost\) pa \(60.0\) %.

Točnost obeh diagnostičnih sistemov lahko izračunamo iz kontingenčnih tabel po obrazcu \(točnost = (TP+TN) / N\). V primeru prvega diagnostičnega sistema znaša \(točnost = (26+13)/51 = 76.5\) %, v drugem primeru pa \(točnost = (21+14)/51 = 68.6\) %.

Končne ugotovitve

Z izvedbo kontingenčne tabele smo izračunali senzitivnost, specifičnost in točnost dveh testnih diagnostičnih sistemov v primerjavi z dejansko diagnozo.

V primeru prvega diagnostičnega sistema smo izračunali senzitivnost = 81.3 %, specifičnost = 74.3 % ter točnost = 76.5 %. V primeru drugega diagnostičnega sistema smo izračunali senzitivnost = 87.5 %, specifičnost = 60.0 % ter točnost = 68.6 %. Na podlagi rezultatov lahko ugotovimo, da ima drugi sistem višjo senzitivnost na račun nižje specifičnosti v primerjavi s prvim diagnostičnim sistemom.

Vendar pa s pomočjo izračunanih mer ne moremo določiti, kateri sistem je boljši, zato smo izračunali še točnost obeh sistemov, pri čemer smo ugotovili višjo točnost prvega diagnostičnega sistema (76.5 %) v primerjavi s točnostjo drugega diagnostičnega sistema (68.6 %).

Hkrati je potrebno opozoriti, da sta meri senzitivnost in specifičnost povezani - ko eno povišujemo, se druga niža in obratno. Točnost je ustrezna mera za primerjavo, če je pozitivnih in negativnih primerov približno enako, sicer pa tudi točnost lahko ‘popravljamo’ tako, da napovedujemo več tistih diagnoz, ki jih je več.

3.2 Krivulja ROC

Navodila vaje

V datoteki kreatinin_akin.sav imamo podatke o pacientih po operaciji srca z okvaro delovanja ledvic (Kališnik et al. 2017). Pri pacientih merimo kreatinin pred in po operaciji in poznamo diagnozo okvare delovanja ledvic.

1. Ugotovi, katera izmed meritev kreatinina dobro napove okvaro ledvic.

   To naredi z izdelavo ROC krivulje.

2. Izračunaj AUC in primerjaj AUC obeh krivulj ter komentiraj rezultate.

3. Določi tudi ‘optimalno’ vrednost kreatinina, s katero boš dosegel najboljšo specifičnost in senzitivnost (t.i. Youden cut-off point (Youden 1950)).

Postopek reševanja

Odpremo podatke, zapisane v SPSS datoteki, s programom Jamovi. Open -> kreatinin_akin.sav.

To so dejanski podatki o pacientih po operaciji na srcu, kjer smo jim merili različne parametre, med drugim tudi kreatinin pred operacijo in kreatinin en dan po operaciji. Del podatkov je prikazan v nadaljevanju:

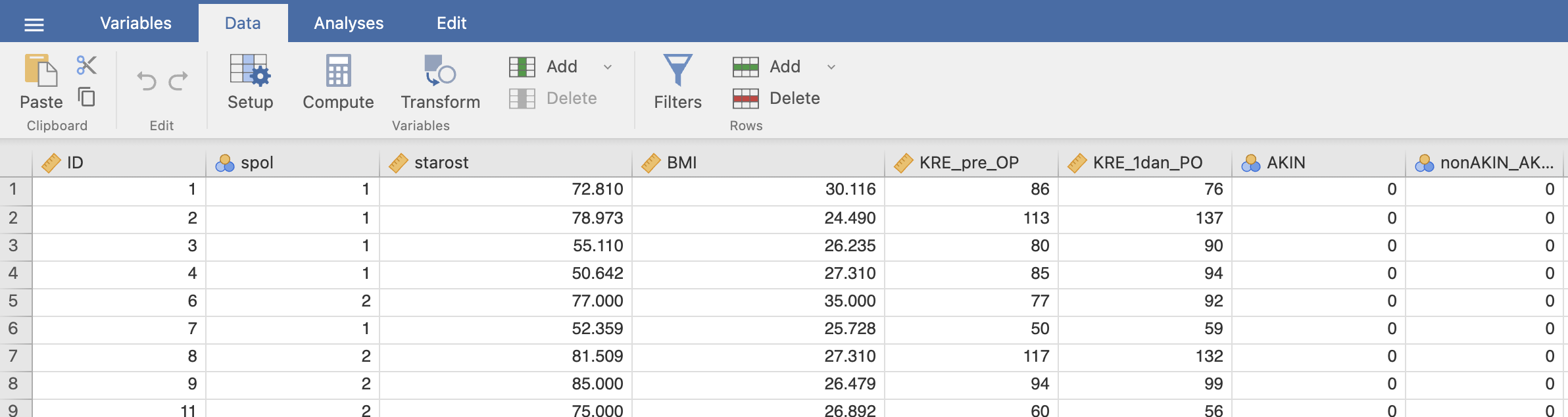
V našem primeru nas zanimajo spremenljivke KRE_pre_OP, kjer imamo meritve kreatinina pred operacijo, spremenljivka KRE_1dan_PO, kjer imamo meritve kreatinina pri pacientih en dan po operaciji in spremenljivka nonAKIN_AKIN, kjer imamo dejanske diagnoze okvare delovanja ledvic, pri čemer vrednost 1 pomeni okvaro delovanja ledvic, 0 pa ne. Skupaj imamo 263 pacientov.

V tem primeru predstavlja dejansko diagnozo spremenljivka nonAKIN_AKIN, testne diagnoze pa spremenljivki KRE_pre_OP in KRE_1dan_PO, ki sta skalarja. V takšnem primeru testiramo uspešnost napovedovanja dejanske diagnoze z binomsko odločitvijo (odločitvijo, kjer sta možna le dva izida: P ali N, 0 ali 1 ipd.) z uporabo krivulje ROC.

V programu Jamovi moramo najprej dodati nov modul z ukazom +Modules, kjer izberemo jamovi library:

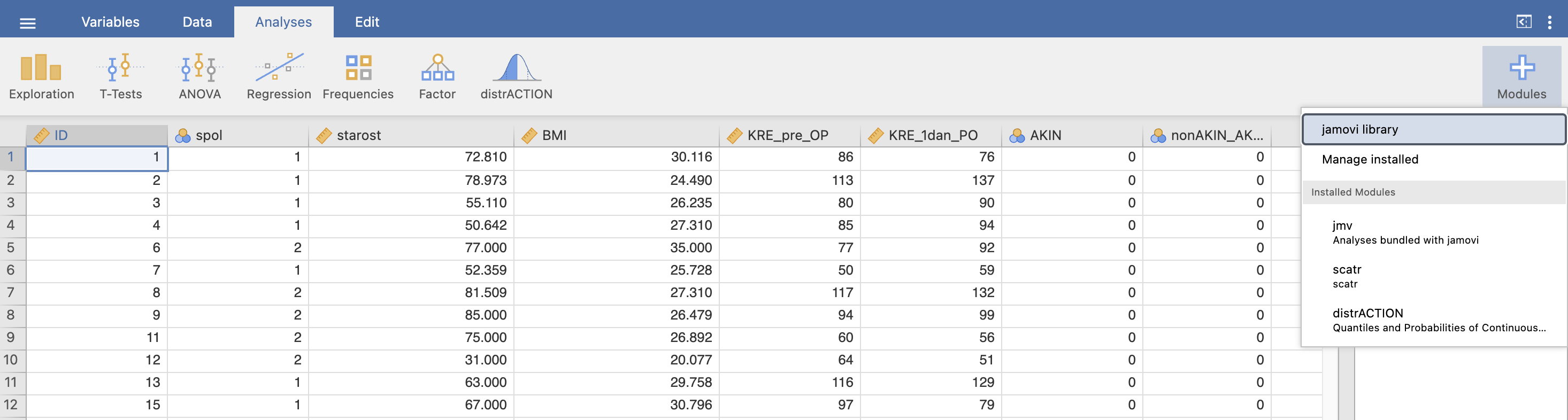
V knjižnici modulov poiščemo modul psychoPDA in ga namestimo v program:

Po namestitvi se nam nov modul (PPDA) pokaže v orodni vrstici programa Jamovi:

Analizo z ROC krivuljo izvedemo z izbiro Analyses -> PPDA in pod Measure Diagnostics izberemo Test ROC.

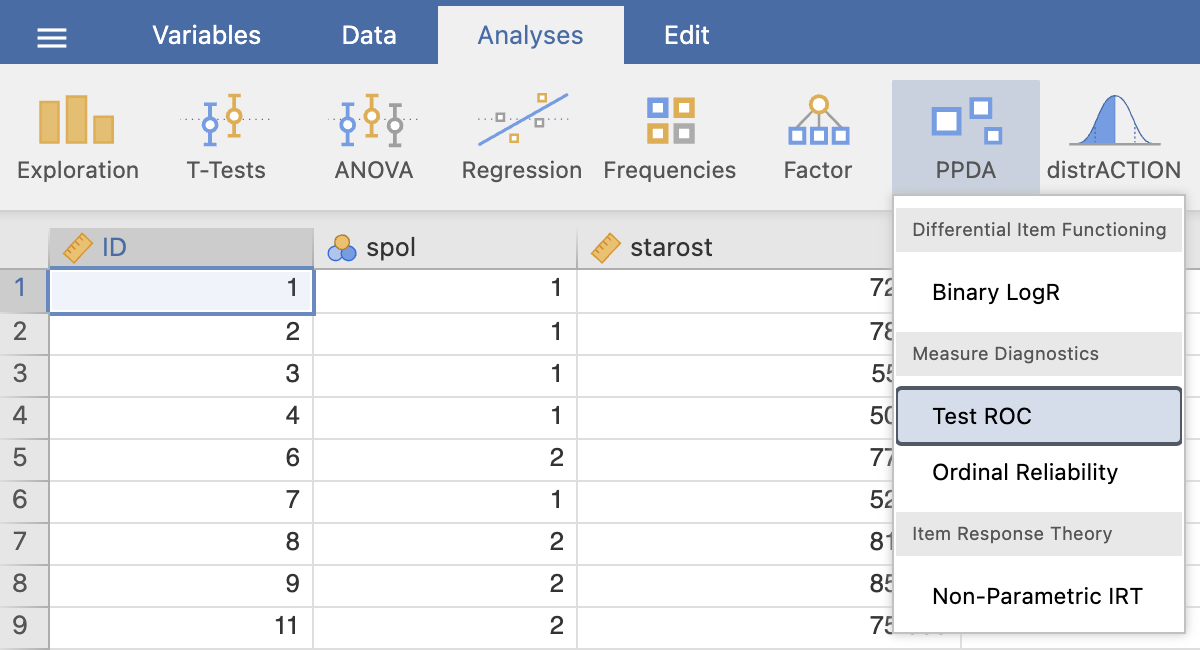
V levem oknu za Dependent Variable izberemo spremenljivko KRE_pre_OP, ki predstavlja testno diagnozo, kot Class Variable pa izberemo spremenljivko nonAKIN_AKIN, ki predstavlja dejansko diagnozo. Pri Positive class določimo, katera vrednost spremenljivke predstavlja pozitivno diagnozo (1).

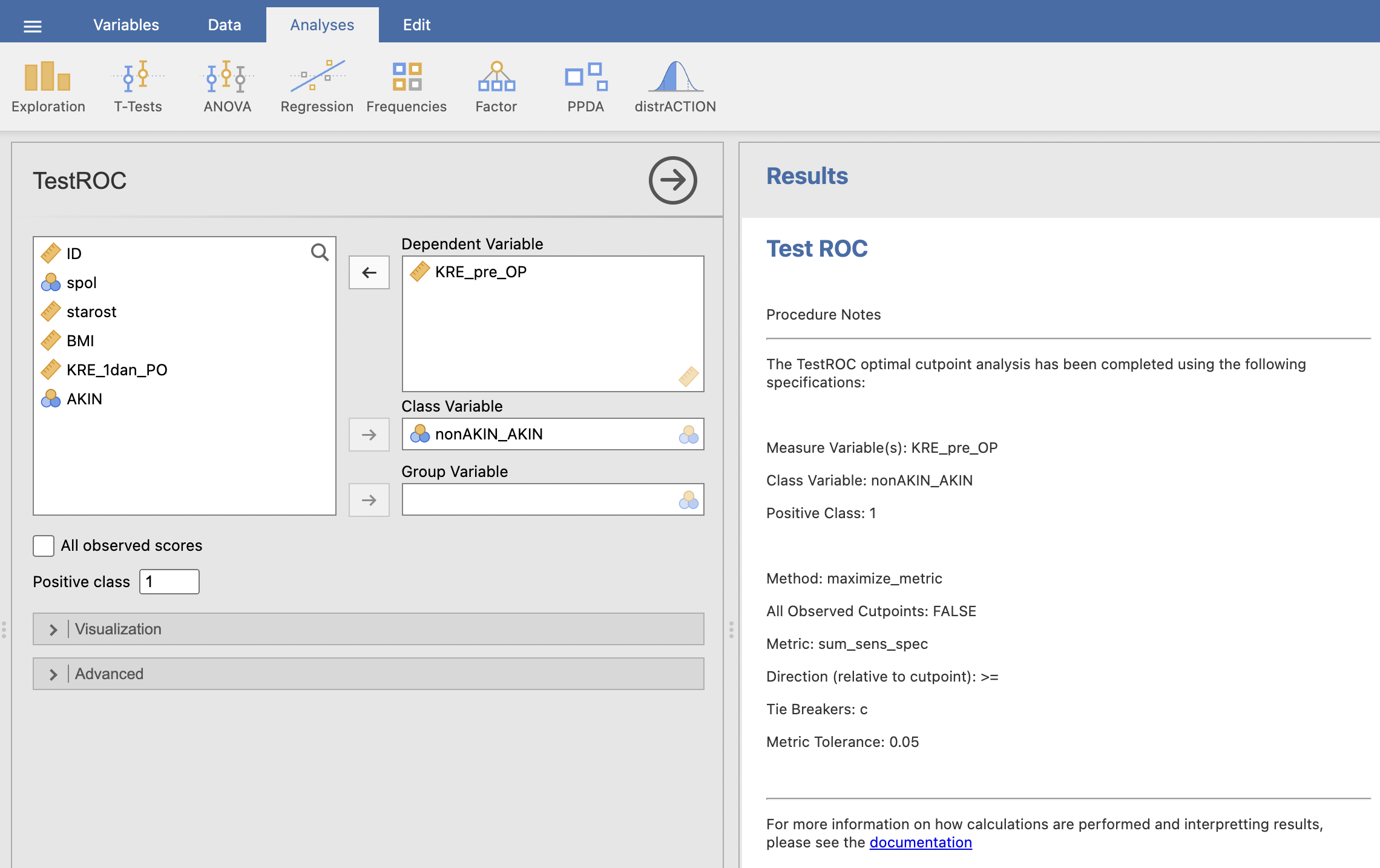
V desnem oknu Results se nam izriše ROC krivulja in izpiše tabela mejnih vrednosti.

Iz tabele lahko razberemo vrednost ploščine pod krivuljo (AUC) in s pomočjo Youden-ovega indeksa določimo optimalno vrednost kreatinina, s katero dosežemo najboljšo specifičnost in senzitivnost. Po (Youden 1950) sta optimalna senzitivnost in specifičnost doseženi, ko je njuna vsota največja. Youden-ov indeks je enak \((senzitivnost + specifičnost) - 1\).

Vrednost \(AUC = 0.406\), optimalna vrednost kreatinina pa je enaka \(121.0\). To vrednost smo razbrali iz stolpca Cutpoint, pri kateri je Youden’s index najvišji (0.05376). Senzitivnost je pri tej vrednosti enaka 0.100, specifičnost pa 0.954, skupna vsota je 1.054.

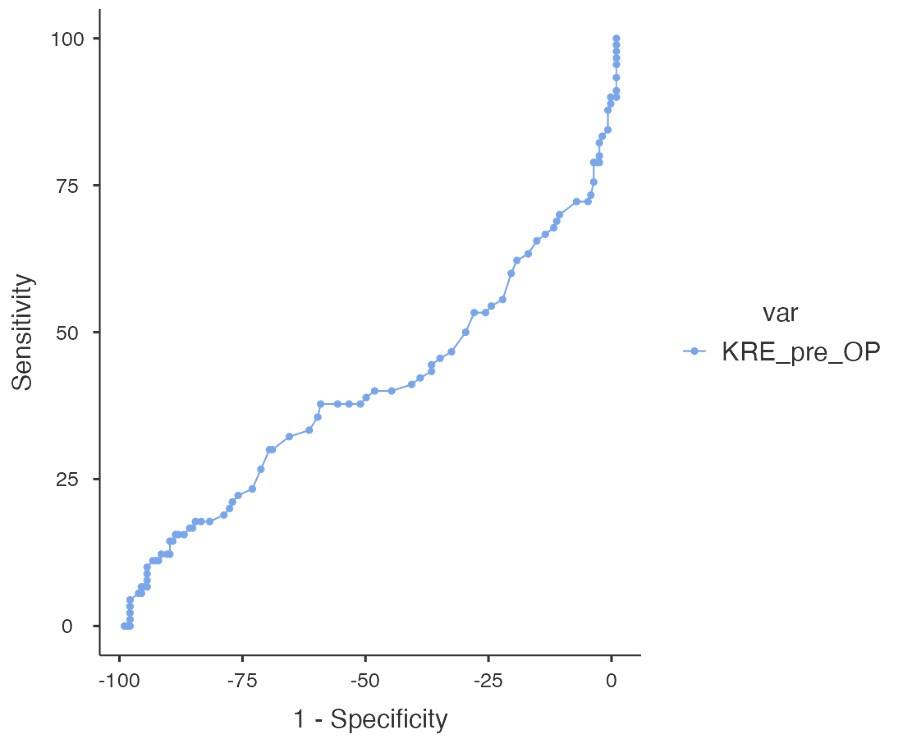
Enako ponovimo še za spremenljivko KRE_1dan_PO: Analyses -> PPDA in pod Measure Diagnostics izberemo Test ROC.

V levem oknu za Dependent Variable izberemo spremenljivko KRE_1dan_PO, ki predstavlja testno diagnozo, kot Class Variable pa izberemo spremenljivko nonAKIN_AKIN, ki predstavlja dejansko diagnozo. Pri Positive class določimo, katera vrednost spremenljivke predstavlja pozitivno diagnozo (1).

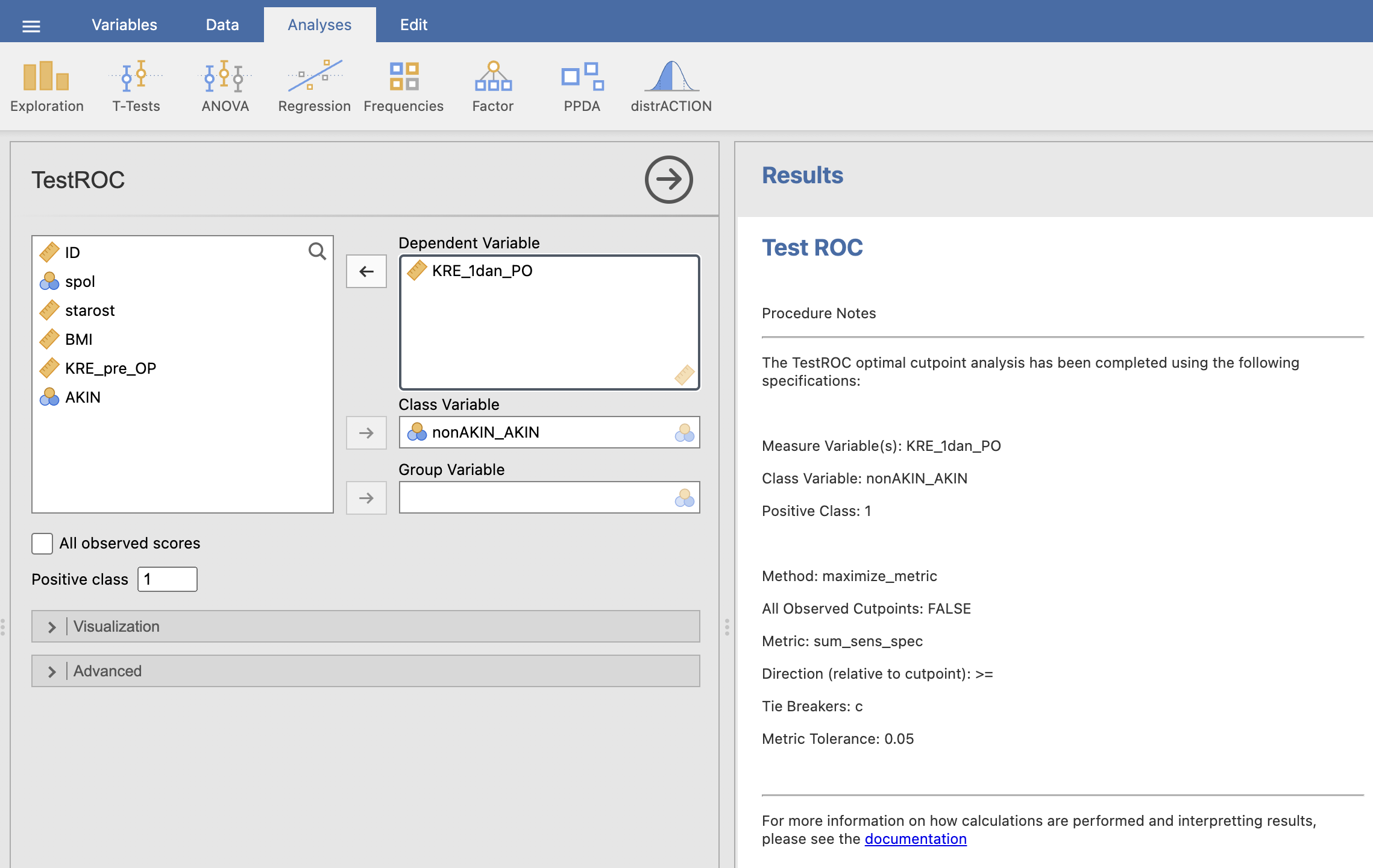
V desnem oknu Results se nam izriše ROC krivulja in izpiše tabela mejnih vrednosti.

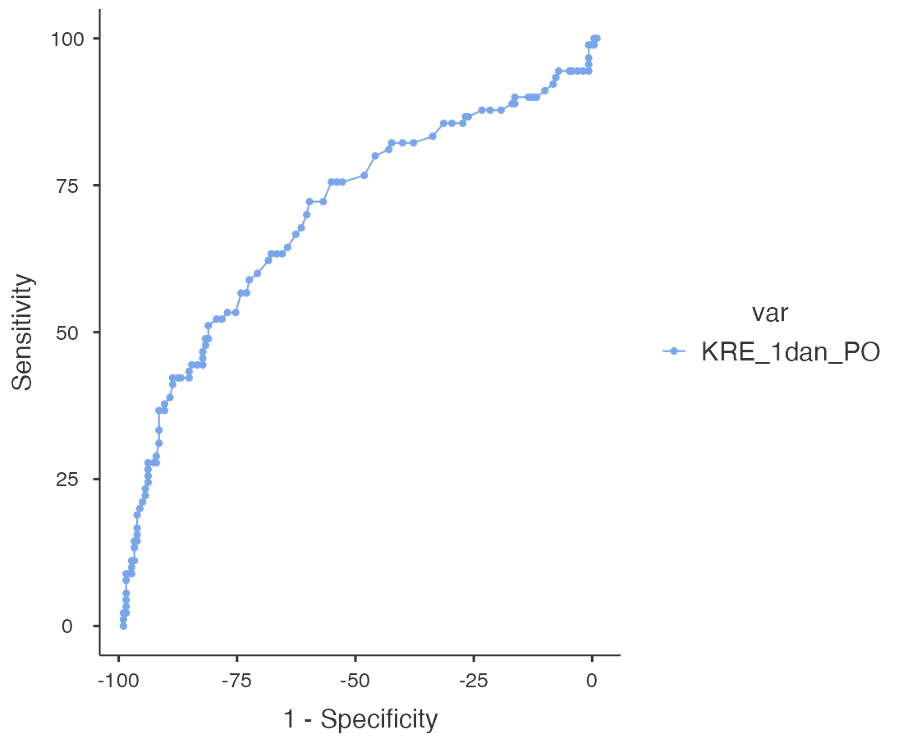
Iz tabele razberemo željene vrednosti.

Vrednost \(AUC = 0.702\), optimalna vrednost kreatinina pa je enaka \(87.0\). To vrednost smo razbrali iz stolpca Cutpoint, pri kateri je Youden’s index najvišji (0.329). Pri tej vrednosti imamo senzitivnost = 0.722 in specifičnost = 0.607, skupna vsota je 1.329.

Končne ugotovitve

Z ROC analizo smo ugotavljali, katera meritev kreatinina je uspešnejša pri napovedovanju motenj delovanja ledvične funkcije. Izrisali smo ROC krivulje in izračunali AUC za meritve kreatinina pred in po operaciji pri diagnozi okvare ledvične funkcije.

Ugotovili smo, da meritve kreatinina pred operacijo neuspešno diagnosticirajo okvaro ledvic, saj je vrednost AUC = 0.406, kar je slabše kot če bi naključno določevali diagnozo. Glede na rezultate kreatinin, ki je merjen 1 dan po operaciji, bolje diagnosticira okvaro delovanja ledvic, saj je AUC = 0.702.

Pri vrednostih kreatinina smo računali mejno vrednost kreatinina za optimalno senzitivnost in specifičnost po Youdenu. Ugotovili smo, da je optimalen prag kreatinina pred operacijo 121.0, pri čemer dobimo senzitivnost določanja okvare ledvic 0.100 in specifičnost 0.954. Mejna vrednost kreatinina 1 dan po operaciji pa je pri 86.5, pri čemer dobimo senzitivnost 0.722 in specifičnost 0.607.

3.3 Ujemanje med ocenjevlaci – koeficient kappa

Navodila vaje

V datoteki oznacevanje_artefaktov.sav so zbrane ocene označevanja artefaktov na mamografskih slikah (Žibert et al. 2016). Slike sta označevala dva označevalca.

1. Ugotovi stopnjo ujemanja označevanja med označevalcema pri vsakem tipu artefakta posebej:

   1. Najprej izračunaj točnost ujemanja med obema označevalcema.
   2. Nato izračunaj Cohenov koeficient kappa in komentiraj rezultate.
   3. Kaj predstavljajo kapa koeficienti?

Postopek reševanja

V programu Jamovi preberemo podatke iz naloge za statistično analizo: Open in najdemo datoteko oznacevanje_artefaktov.sav.

Podatki so organizirani tako, kot je prikazano na spodnji sliki:

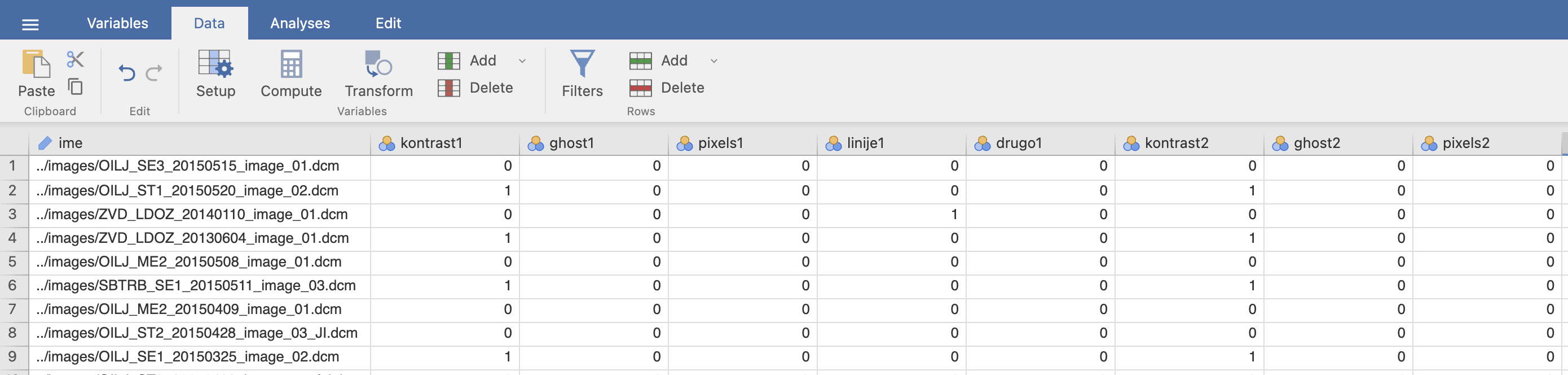
Vsaka mamografska slika je bila ocenjena s strani dveh označevalcev, ki sta na slikah označevala prisotnost artefaktov: kontrasta (spr. kontrast), ghost-a (spr. ghost), skupkov mrtvih pikslov (spr. pixels), linije (spr. linije) in drugo (spr. drugo). Označevalec 1 ima ocene zapisane v spremenljivkah z dodano številko 1, označevalec 2 pa v spremenljivkah z dodano številko 2. Če je na sliki prisoten artefakt, je vrednost spremenljivke 1, sicer je 0.

Izračun stopnje ujemanja med označevalcema izračunamo z uporabo Cohenovega koeficienta kappa. V programu Jamovi moramo najprej dodati nov modul z ukazom +Modules, kjer izberemo jamovi library:

V knjižnici modulov poiščemo modul meddecide in ga namestimo v program:

Po namestitvi se nam nov modul (meddecide) pokaže v orodni vrstici programa Jamovi:

Za izračun Cohenovega koeficienta kappa, izvedemo ukaz Analyses -> meddecide in pod Agreement izberemo Interrater Reliability.

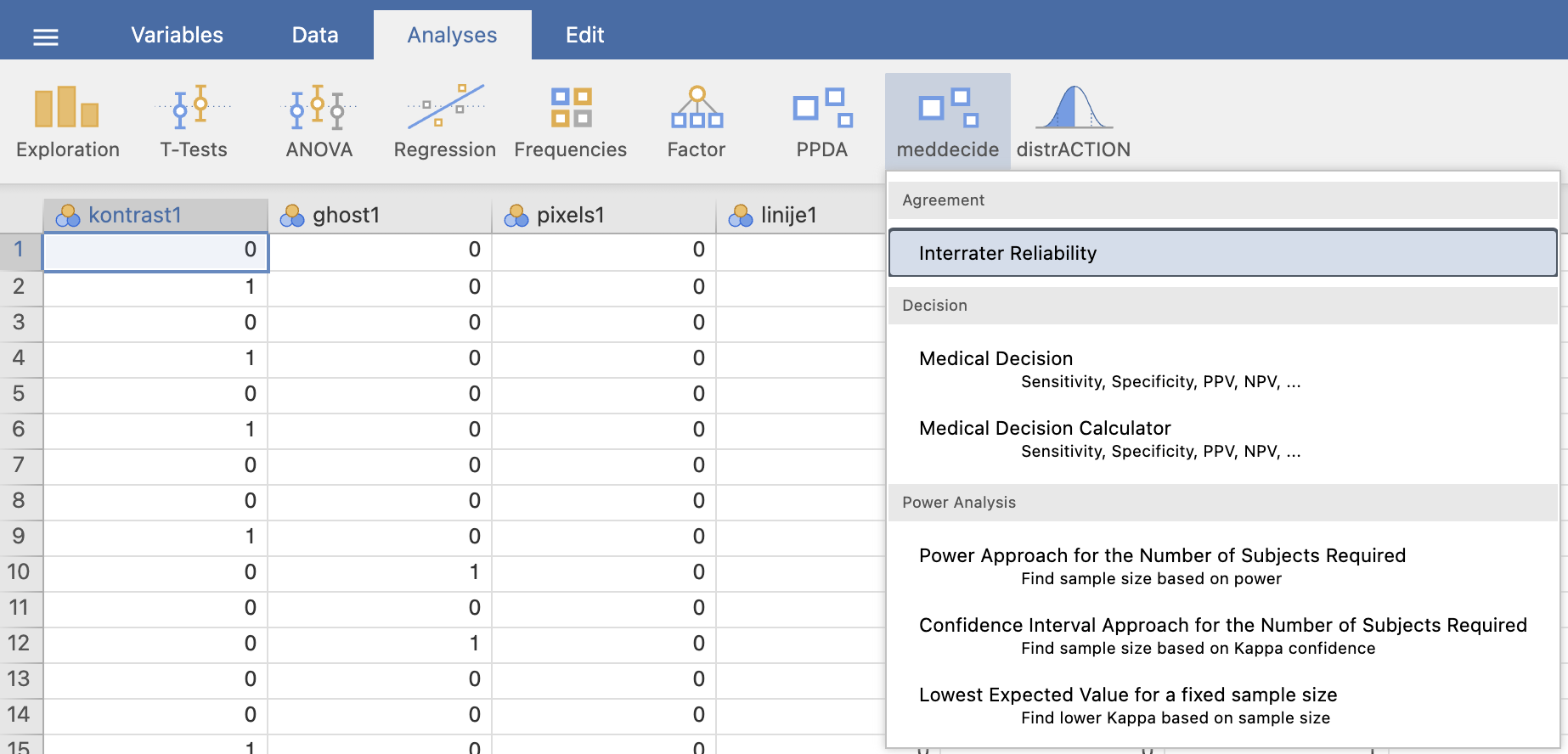
V levem oknu izberemo ustrezne spremenljivke za izračun kappa koeficienta in izris kontingenčne tabele. Najprej bomo preverili ujemanje označevalcev pri ocenjevanju kontrasta, zato pod Raters izberemo spremenljivki kontrast1 in kontrast2. Za izpis kontingenčne tabele pod razdelkom Table označimo možnost Frequency Tables.

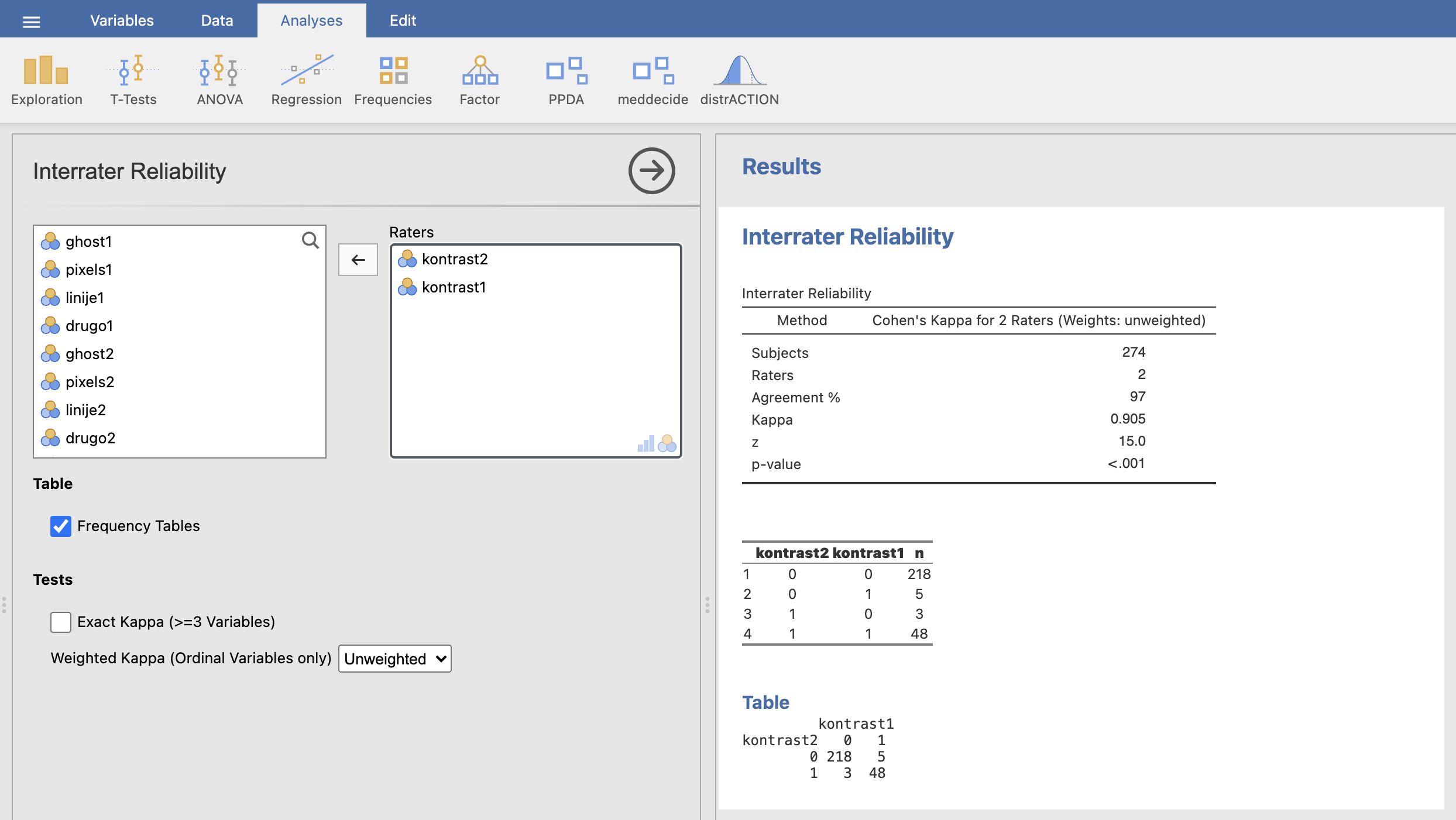
Enak postopek ponovimo za ujemanje označevalcev v ostalih artefaktih, le da namesto spremenljivk kontrasta vpišemo spremenljivke ghost, pixels, linije in drugo.

V desnem oknu Results smo tako dobili kontingenčne tabele, izračunano točnost ujemanja med označevalcema (pod Agreement %) in koeficiente kappa za vsak artefakt posebej:

Artefakt kontrast:

Artefakt ghost:

Artefakt piksli:

Artefakt linije:

Artefakt drugo:

Končne ugotovitve

Izračunani koeficient kappa za ujemanje označevalcev pri ocenjevanju artefakta kontrast je \(\kappa = 0.905\). Točnost njunega ujemanja je 97 %, pri čemer se nista ujemala v 8 oznakah od 274 slik.

Izračunani koeficient kappa za ujemanje označevalcev pri ocenjevanju artefakta ghost je \(\kappa = 0.761\). Točnost njunega ujemanja je 95 %, pri čemer se nista ujemala v 13 oznakah od 274 slik.

Izračunani koeficient kappa za ujemanje označevalcev pri ocenjevanju artefakta piksli je \(\kappa = 0.329\). Točnost njunega ujemanja je 99 %, pri čemer se nista ujemala v 4 oznakah od 274 slik.

Izračunani koeficient kappa za ujemanje označevalcev pri ocenjevanju artefakta linije je \(\kappa = 0.757\). Točnost njunega ujemanja je 95 %, pri čemer se nista ujemala v 15 oznakah od 274 slik.

Izračunani koeficient kappa za ujemanje označevalcev pri ocenjevanju artefakta drugo je \(\kappa = 0.975\). Točnost njunega ujemanja je 100 %, pri čemer se nista ujemala v 1 oznaki od 274 slik.

Tako lahko ugotovimo skoraj popolno ujemanje označevalcev pri artefaktih kontrast in drugo, dobro ujemanje pri artefaktih ghost in linije in slabše ujemanje pri artefaktu piksli, kjer pa je prišlo do slabega ujemanja predvsem zaradi tega, ker je artefaktov piksli na slikah zelo malo (označevalec 1 je označil 5 slik s prisotnim artefaktom piksli, označevalec 2 pa samo eno).

3.4 Koeficient kappa – več možnih oznak

Navodila vaje

V datoteki oznacevanje_3eksperti.xlsx so zbrani podatki o označevanju treh ekspertov, ki so na podlagi slik postavljali diagnoze: normalno (N), sumljivo (S), patologija (P).

1. Oceni ujemanje 3 ekspertov po parih z uporabo koeficientov kappa.

   1. Kaj lahko na podlagi kappa koeficientov povemo o ujemanju med ocenjevalci?
   2. Zakaj so vrednosti koeficientov kappa nižje kot v primeru vaje iz pog. 3.3, ko sta imela označevalca samo dve možnosti?

Postopek reševanja

V programu Jamovi preberemo podatke iz naloge za statistično analizo: Open in najdemo ustrezno datoteko oznacevanje_3eksperti.xlsx.

Podatki so organizirani tako, kot je prikazano na spodnji sliki:

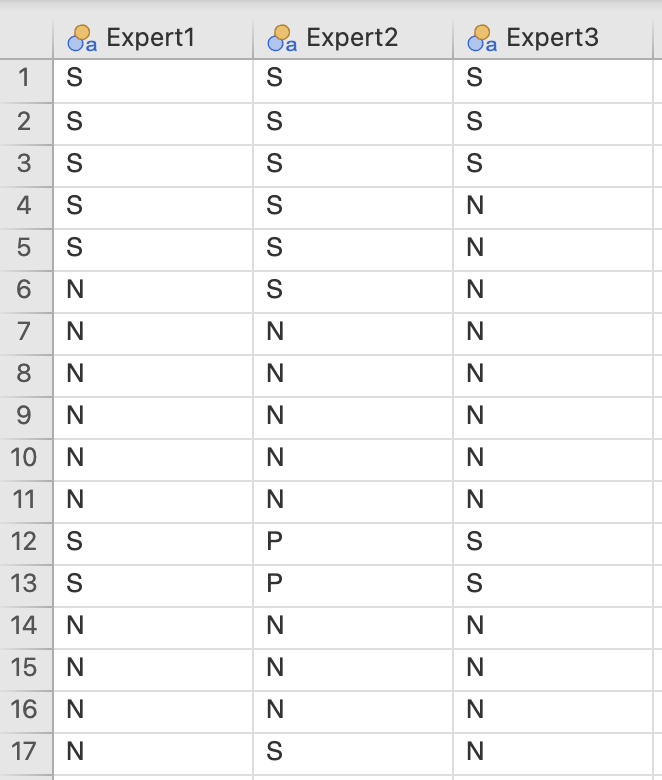
Imamo tri eksperte, ki so na podlagi radioloških slik podajali diagnoze: normalno (N), sumljivo (S), patologija (P). Tako so iz vsake slike pridobljene tri diagnoze.

Ujemanje med eksperti bomo izračunali po parih: ekspert1 : ekspert2, ekspert1 : ekspert3, ekspert2 : ekspert3. Izračunali bomo koeficiente kappa in na podlagi tega določili, kdo se boljše ujema in kako.

Analyses -> meddecide in pod Agreement izberemo Interrater Reliability.

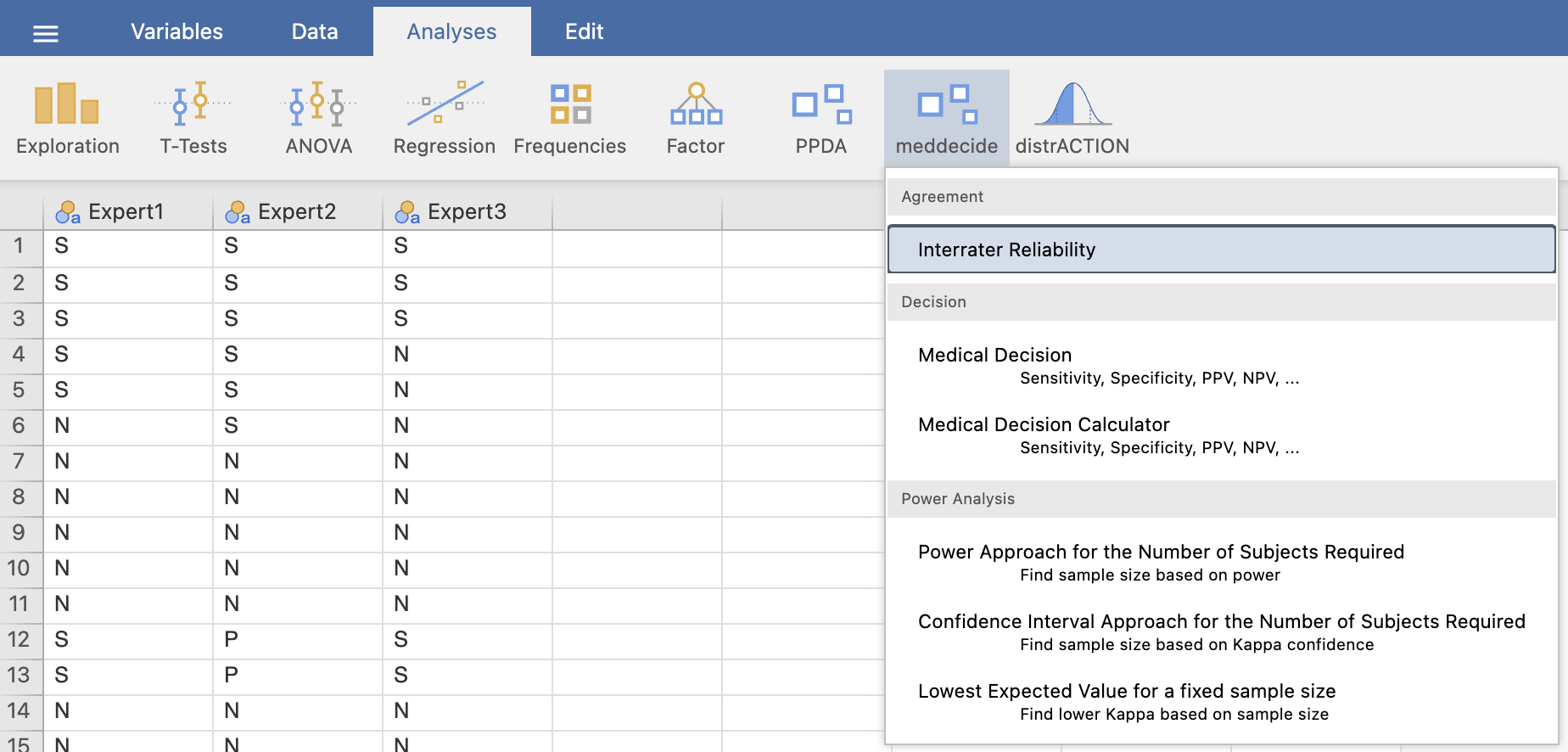
V levem oknu izberemo ustrezne spremenljivke za izračun kappa koeficienta in izris kontingenčne tabele. Najprej bomo preverili ujemanje eksperta 1 in eksperta 2, zato pod Raters izberemo spremenljivki Expert1 in Expert2. Za izpis kontingenčne tabele pod razdelkom Table označimo možnost Frequency Tables.

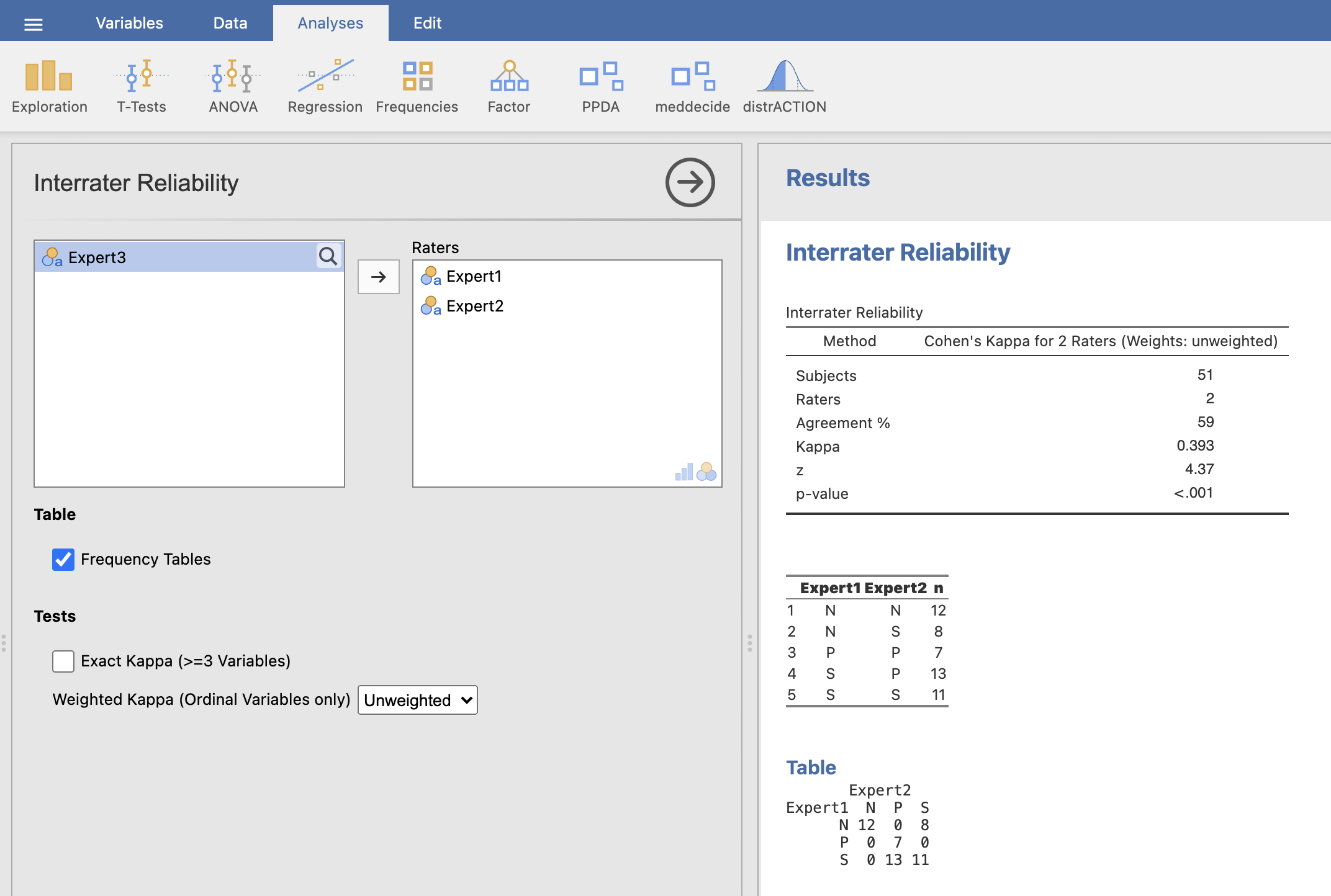
Enak postopek ponovimo za ujemanje eksperta 1 in 3 ter eksperta 2 in 3 tako, da v Raters vstavljamo ustrezne spremenljivke.

V desnem oknu Results dobimo kontingenčne tabele in koeficiente kappa za vsak par ekspertov posebej:

Ekspert 1 proti ekspert 2:

Ekspert 1 proti ekspert 3:

Ekspert 2 proti ekspert 3:

Končne ugotovitve

Izračunani koeficient kappa za ujemanje eksperta 1 in eksperta 2 pri diagnosticiranju 51 slik je \(\kappa = 0.393\).

Izračunani koeficient kappa za ujemanje eksperta 1 in eksperta 3 pri diagnosticiranju 51 slik je \(\kappa = 0.532\).

Izračunani koeficient kappa za ujemanje eksperta 2 in eksperta 3 pri diagnosticiranju 51 slik je \(\kappa = 0.318\).

Tako lahko ugotovimo, da se eksperta 1 in 3 boljše ujemata pri diagnosticiranju, ekspert 2 pa ima slabše ujemanje z ostalima ekspertoma.

Ugotovimo lahko tudi, da imamo precej slabše vrednosti kappa koeficientov kot pri vaji 3, ko so označevalci izbirali samo med dvema oznakama (artefakt je ali ga ni). V predstavljenem primeru pa imamo tri izbire normalno (N), sumljivo (S) in patologija (P).

V primeru večih izbir so vrednosti koeficientov kappa nižje. Problem pri računanju ujemanja, ki se pogosto pojavlja v diagnostiki, je vmesna oznaka sumljivo (S), ki se precej meša med oznakama normalno (N) in patologija (P). Tudi zaradi tega so vrednosti kappa koeficienta nižje.

V primeru, ko imamo vrednosti izbire, ki se lahko bolj mešajo med seboj, je potrebno napake med označevanji ustrezno kaznovati (penalizirati). V našem primeru bi lahko bolj kaznovali napako neujemanja N in P (npr. z utežjo 2) in manj kaznovali neujemanje S in P ter S in N (npr. z utežjo 1). Tako bi lahko tudi izračunali koeficient kappa, ki ga zaradi različnih uteži imenujemo uteženi koeficient kappa.

Kališnik, Jurij Matija, Eva Hrovat, Alenka Hrastovec, Janez Žibert, Aleš Jerin, Milan Skitek, Giuseppe Santarpino, and Tomislav Klokocovnik. 2017. “Creatinine, Neutrophil Gelatinase-Associated Lipocalin, and Cystatin c in Determining Acute Kidney Injury After Heart Operations Using Cardiopulmonary Bypass.” Artificial Organs 41 (5): 481–89. https://doi.org/https://doi.org/10.1111/aor.12779.

Youden, W. J. 1950. “Index for Rating Diagnostic Tests.” Cancer 3 (1): 32–35. https://doi.org/https://doi.org/10.1002/1097-0142(1950)3:1<32::AID-CNCR2820030106>3.0.CO;2-3.

Žibert, Janez, Nejc Mekiš, Urban Zdešar, Anja Golja, and Aljaž Iskra. 2016. “Avtomatična Detekcija Artefaktov Na Mamografskih Slikah = Automatic Detection of Artifacts on Mammographic Images.” Bilten : Strokovno in Informativno Glasilo Društva Radioloških Inženirjev Slovenije in Zbornice Radioloških Inženirjev Slovenije 33 (2): 21–26. https://mirtjournal.net/index.php/home/issue/view/72/218.