1 Osnovni pojmi statistične analize
1.1 Priprava podatkov v Jamovi in osnovna opisna statistika
Neko farmacevtsko podjetje testira novo zdravilo za zniževanje temperature. Zanima jih učinkovitost zdravila glede na hitrost zmanjšanja temperature.
V eksperiment so zajeli tri starostne skupine, ki so jih ločili po spolu. V vsaki skupini je bilo 10 udeležencev. Merili so čas v minutah, ko se po zaužitju zdravila telesna temperatura zniža pod dovoljeno mejo. Podatki so v spodnji tabeli:
| Moški | Ženske | |
|---|---|---|
| otroci | 54, 49, 59, 39, 55, 47, 55, 52, 52, 54 | 25, 29, 47, 26, 28, 33, 30, 28, 27, 30 |
| odrasli | 53, 72, 43, 56, 52, 67, 45, 72, 68, 59 | 46, 51, 33, 47, 41, 45, 47, 38, 42, 50 |
| starejši | 33, 30, 26, 25, 29, 31, 34, 27, 33, 28 | 18, 21, 34, 40, 24, 28, 30, 20, 18, 21 |
Podatke organiziraj v Jamovi tako, da jih boš lahko statistično obdelal.
Izvedi osnovno opisno statistiko na podatkih in pravilno poročaj rezultate:
- opisna statistika naj bo izvedena glede na spol,
- glede na starostno skupino in
- glede na oboje skupaj.
- opisna statistika naj bo izvedena glede na spol,
Komentiraj rezultate.
Iz podane tabele ugotovimo, da imamo 3 spremenljivke: spol, starostna skupina in čas. Spol in starostna skupina sta kategorijski spremenljivki, saj imamo pri spolu dve kategoriji: moški, ženska, pri starostni skupini pa tri: otroci, odrasli, starejši. Čas je skalarna spremenljivka.
Odpremo prazen dokument v programu Jamovi in v meniju Variables definiramo spremenljivke tako, kot prikazujejo naslednje slike. Spremenljivko dodamo z izbiro simbola +, ukazom Insert pod Data Variable in z možnostjo Edit uredimo njene lastnosti.
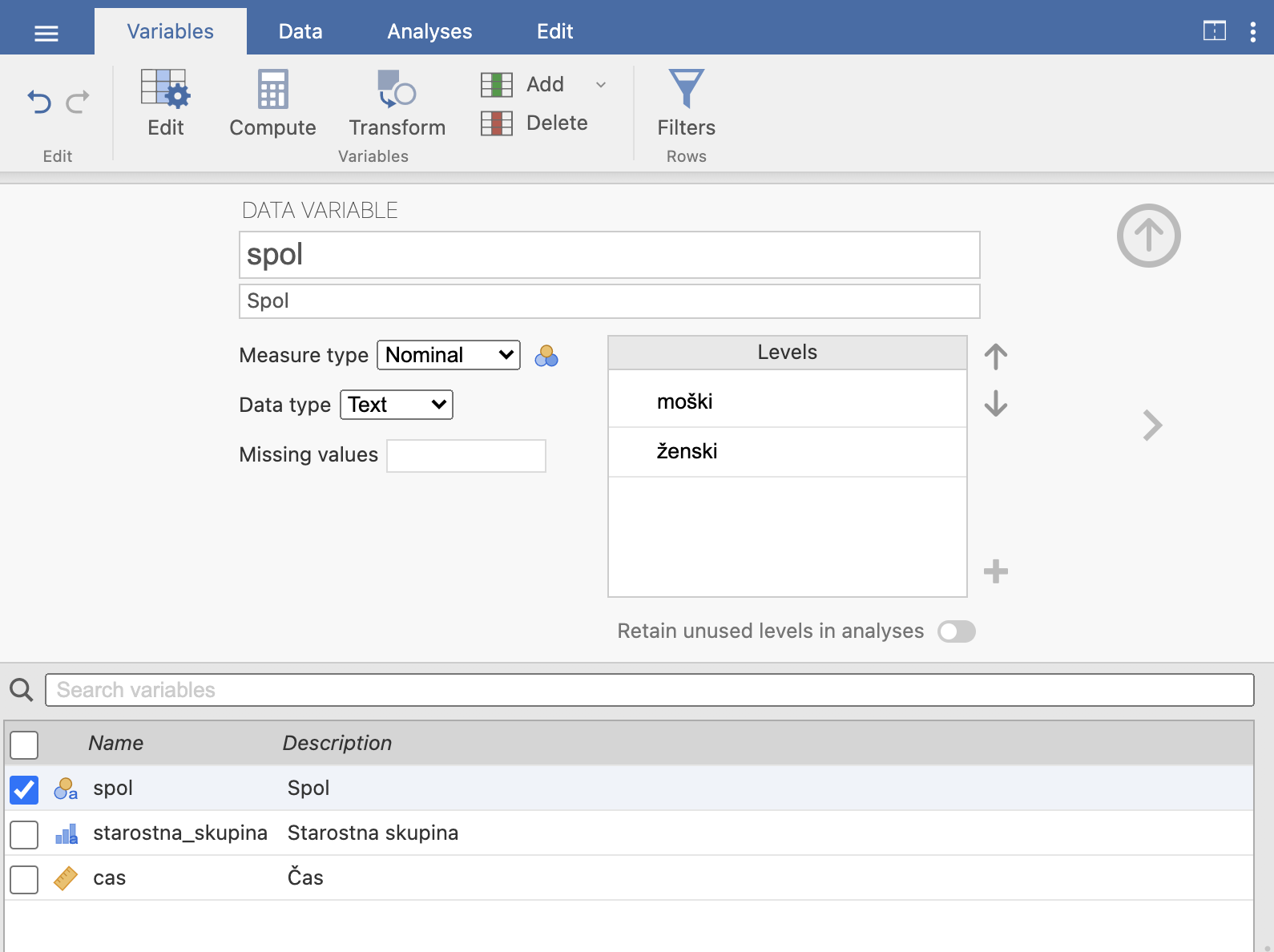
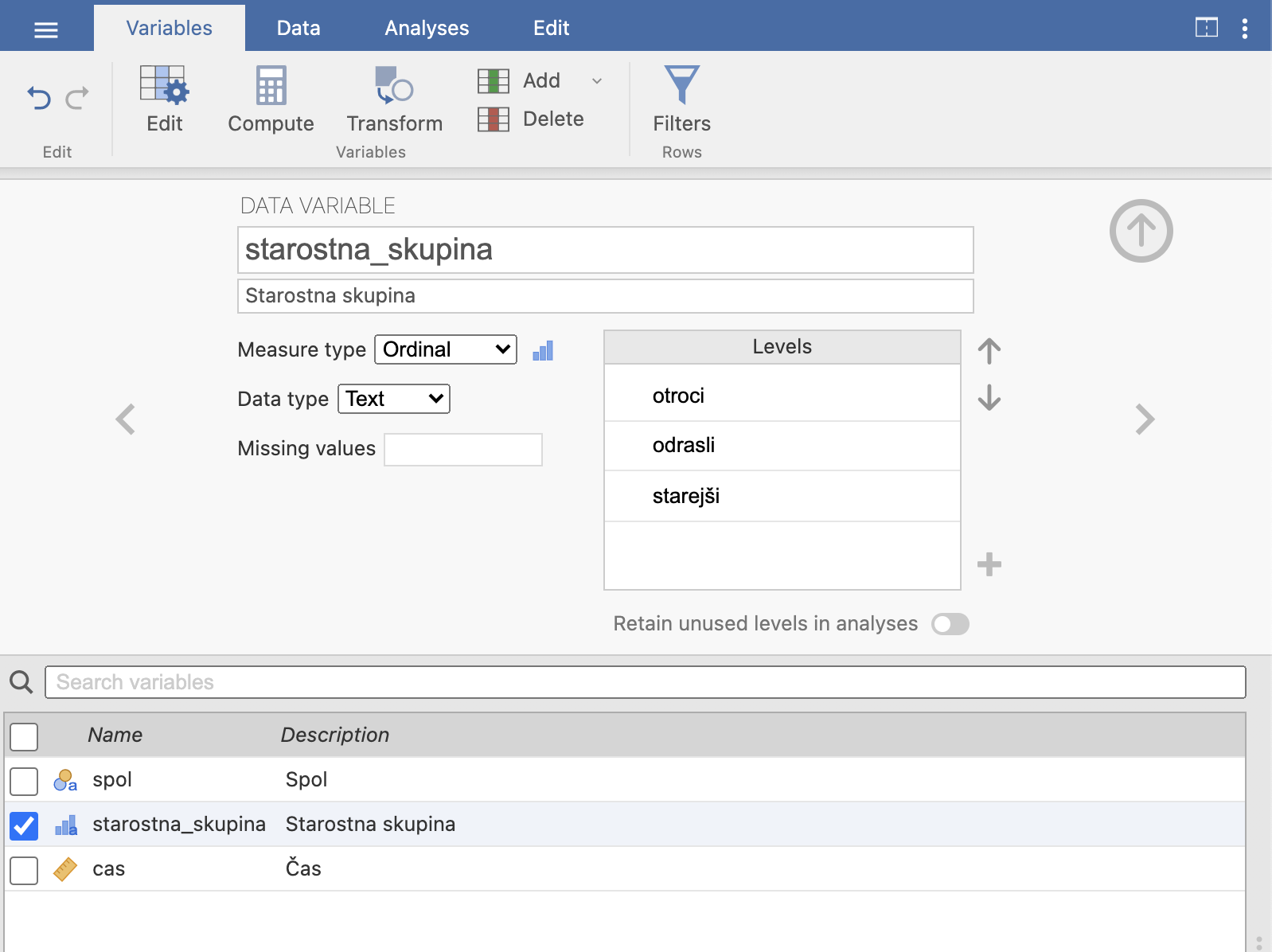
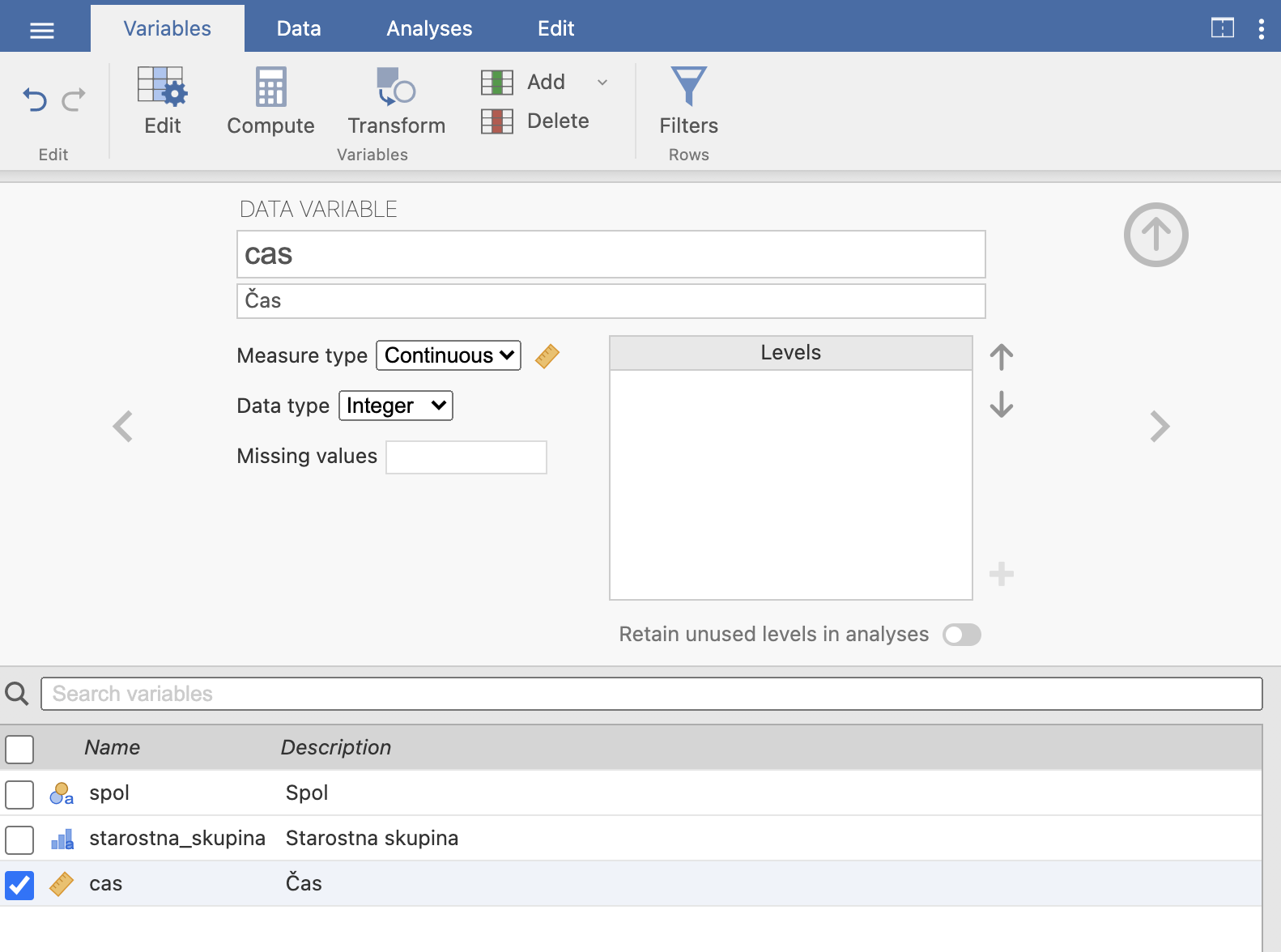
Pri spremenljivkah Spol in Starostna skupina smo določili vrednosti spremenljivke v okencu Levels, pri skalarni spremenljivki Čas pa smo ustrezno označili tip spremenljivke kot Continuous.
Opozoriti velja, da je spremenljivka spol kategorijska nominalna spremenljivka (Nominal), saj njene vrednosti ne morejo biti urejene, kategorijska spremenljivka starostna skupina pa je ordinalna spremenljivka (Ordinal), saj vrednosti spremenljivke lahko urejamo po velikosti.
Ko smo si pripravili spremenljivke, v Data vpišemo podatke iz podane tabele. Imamo izmerjene čase pri šestdesetih osebah, zato mora biti izpolnjenih 60 vrstic. Tabela je organizirana tako, da vsaka vrstica v programu Jamovi predstavlja podatke o eni osebi (to je najbolj priporočljiva organiziranost podatkov v tabelah v zdravstvu).

Ko imamo podatke vpisane, podatke shranimo, da jih lahko potem znova uporabljamo. To naredimo tako, kot je prikazano na spodnji sliki.
Podatki v Jamovi so shranjeni s končnico .omv. Sicer pa lahko podatke izvažamo z ukazom Export v različne formate.
Za izvedbo opisne statistike izberemo: Analyses -> Exploration -> Descriptives
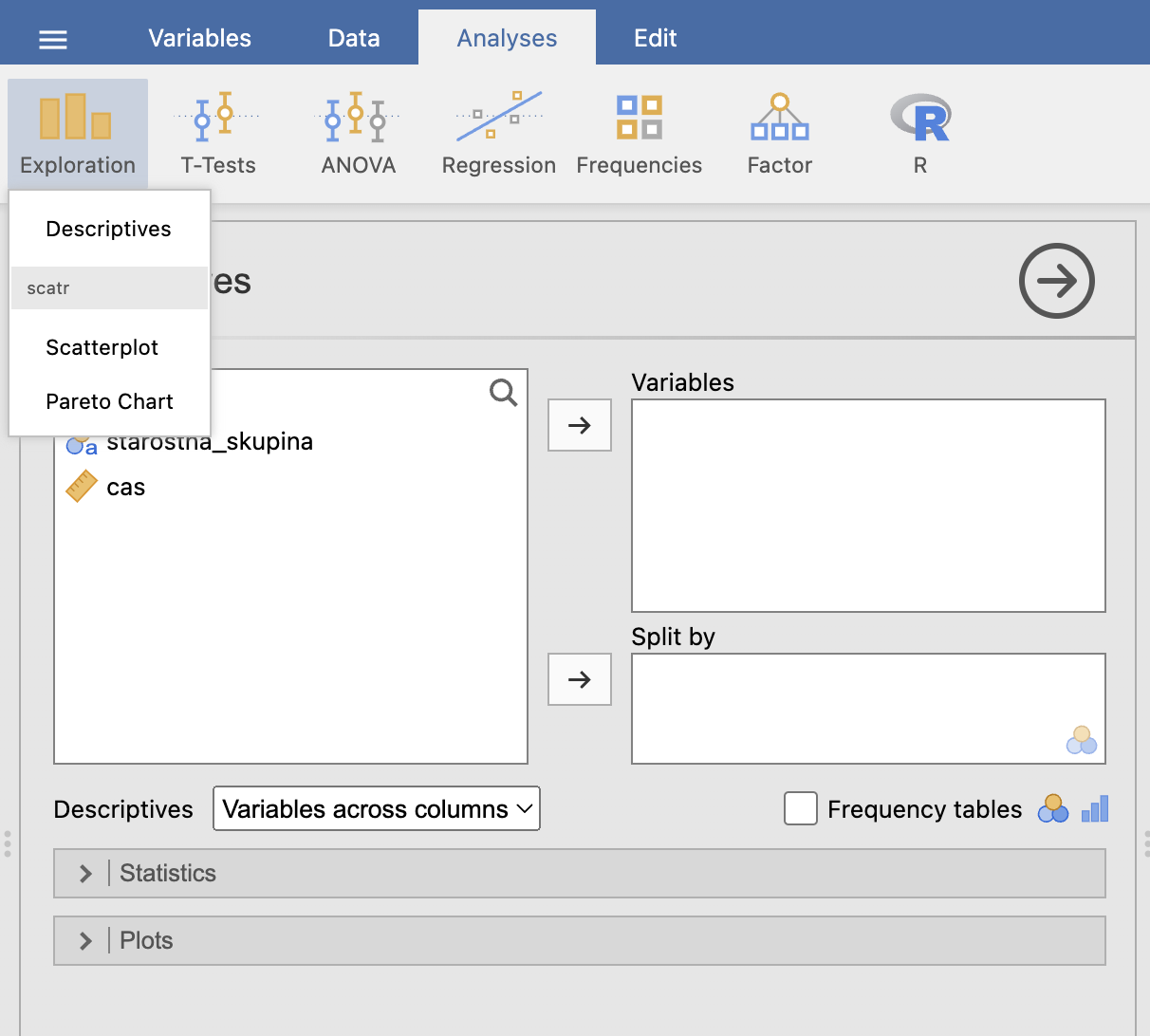
Najprej nas zanima čas v minutah, ko se po zaužitju zdravila telesna temperature zniža pod dovoljeno mejo, glede na spol, zato za Variables izberemo čas, glede na spol, kar izberemo v Split by. V razdelku Statistics pustimo izbrane parametre tako kot so.
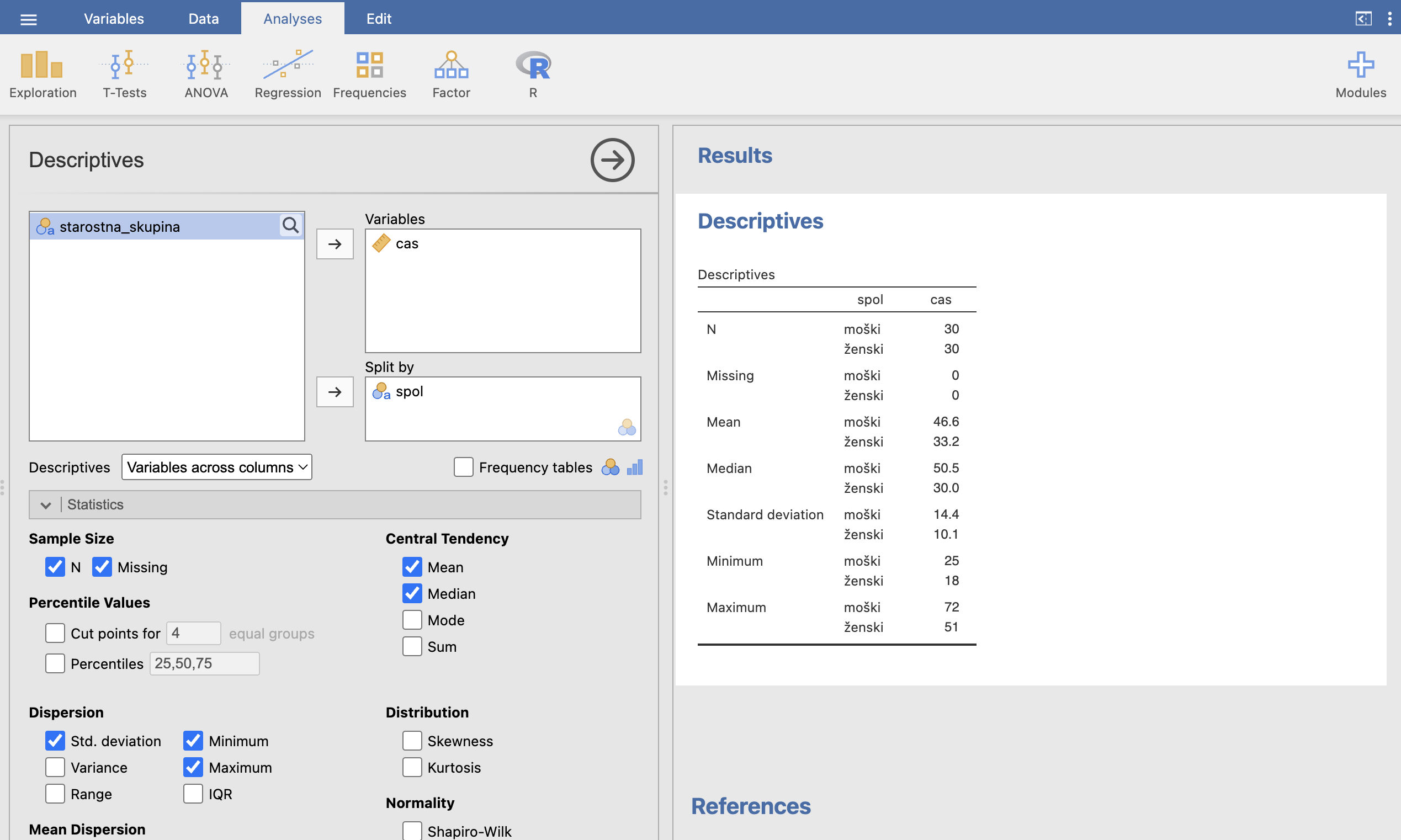
Na desni strani se nam že sproti izračuna izbrana opisna statistika. V tem primeru nas zanimata povprečje in standardni odklon časa glede na spol. Ostale statistike nas v tem primeru ne zanimajo. Iz tabele razberemo povprečje in standardni odklon časa v minutah pri moških in ženskah.
Rezultate lahko predstavimo v naslednji tabeli:
| SPOL | ||
|---|---|---|
| moški | ženski | |
| ČAS [min] | 46.6 ± 14.4 | 33.2 ± 10.1 |
V povprečju se pri moškem spolu po 46.6 ± 14.4 minutah od zaužitja zdravila telesna temperatura zniža pod dovoljeno mejo. Pri ženskem spolu se v povprečju od zaužitja zdravila telesna temperatura zniža pod dovoljeno mejo po 33.2 ± 10.1 minutah. Opazimo, da v povprečju pri moškem spolu zdravilo začne učinkovati po daljšem času kot pri ženskem spolu.
Na podoben način izvedemo opisno statistiko podatkov glede na starostne skupine: Analyses -> Exploration -> Descriptives. Zanima nas povprečni čas v minutah, ko se po zaužitju zdravila telesna temperatura zniža pod dovoljeno mejo, glede na starostno skupino, zato za odvisno spremenljivko (Variables) izberemo čas glede na starostno skupino (Split by).
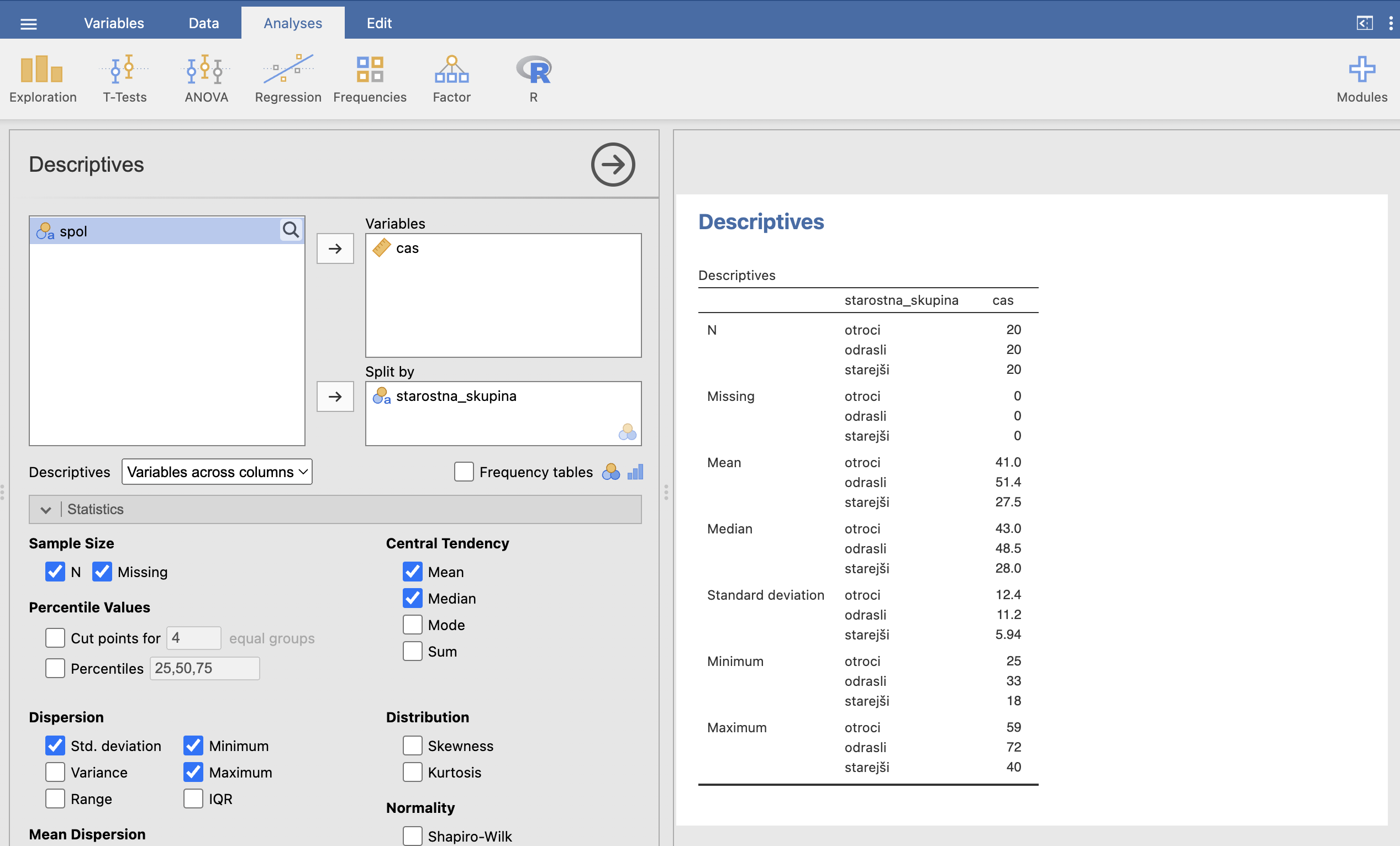
Enako kot prej se nam opisna statistika izračuna na desni strani. Iz tabele opisne statistike izpišemo povprečje in standardni odklon za vsako starostno skupino posebej. Rezultati so predstavljeni v naslednji tabeli:
| STAROSTNA SKUPINA | |||
|---|---|---|---|
| Otroci | Odrasli | Starejši | |
| ČAS [min] | 41.0 ± 12.4 | 51.4 ± 11.2 | 27.5 ± 5.9 |
Ugotovimo, da v povprečju pri starejših zdravilo učinkuje v najkrajšem času, pri odraslih mora v povprečju miniti največ časa. Standardni odkloni nam pokažejo, da pri starejši starostni skupini so izmerjeni časi bolj homogeni (standardni odklon je manjši), pri drugih skupinah izmerjeni časi od zaužitja zdravila do učinkovanja bolj variirajo (standardni odklon je večji).
Zanima nas še čas od zaužitja zdravila do učinkovanja zdravila glede na oba faktorja skupaj (spol in starostne skupine). Zopet izberemo Analyses -> Exploration -> Descriptives, kjer za odvisno spremenljivko (Variables) izberemo čas glede na obe kategorijski spremenljivki (Split by) starostna skupina in spol.
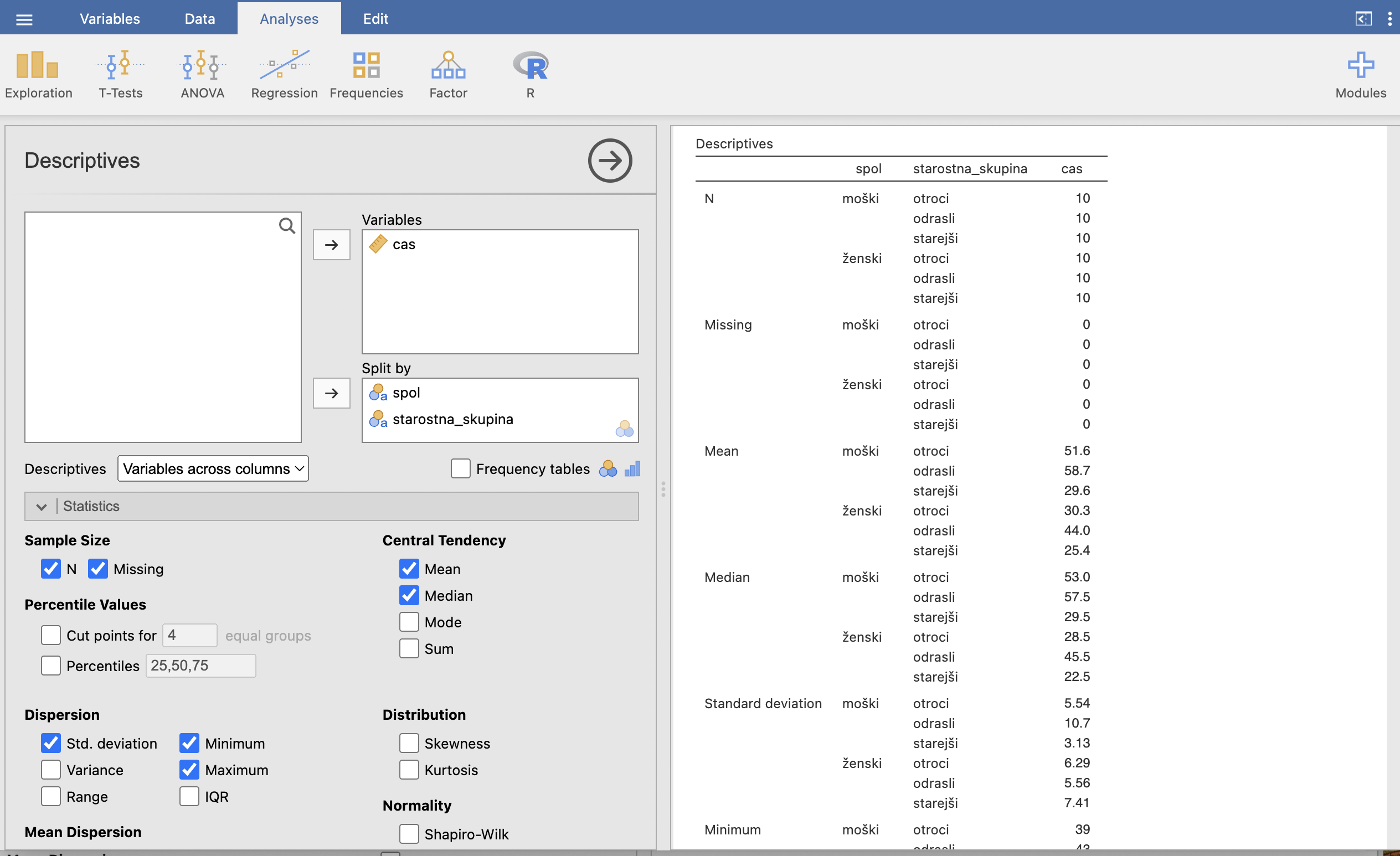
V desnem oknu se nam pripravi tabela, ki pokaže opisno statistiko glede na spol in starostne skupine hkrati. Iz dobljene opisne statistike izpišemo povprečne vrednosti in standardne odklone. Rezultati so predstavljeni v naslednji tabeli:
| STAROSTNA SKUPINA | ||||||
|---|---|---|---|---|---|---|
| Otroci | Odrasli | Starejši | ||||
| SPOL | M | Ž | M | Ž | M | Ž |
| ČAS [min] | 51.6 ± 5.5 | 30.3 ± 6.3 | 58.7 ±10.7 | 44 ± 5.6 | 29.6± 3.13 | 25.4 ± 7.4 |
Primerjamo povprečne čase po spolih pri posameznih starostnih skupinah. Ugotovimo, da obstajajo razlike v povprečnih časih pri otrocih in odraslih med moškimi in ženskami. Povprečni čas učinkovanja zdravila med spoloma pri starejših pa se ne razlikuje toliko kot v ostalih skupinah.
Iz vaje lahko ugotovimo, da novo zdravilo hitreje učinkuje pri ženskemu spolu. Ugotovili smo, da novo zdravilo v povprečju učinkuje najhitreje pri starejših osebah, nato pri otrocih in nazadnje pri odraslih.
Če upoštevamo oba faktorja hkrati, ugotovimo, da pri starejših osebah v povprečju pri obeh spolih zdravilo učinkuje približno enako hitro, pri otrocih in odraslih pa zdravilo v povprečju učinkuje prej pri ženskah kot pri moških.
Pri vaji smo organizirali podatke v Jamovi tako, da smo natančno opredelili spremenljivke v meritvah in da so bile meritve predstavljene v vrsticah po osebah, kar nam je omogočilo ustrezne analize s programom Jamovi.
1.2 Grafi pri statistični analizi
Na podlagi podatkov iz vaje iz pog. 1.1:
Definiraj osnovna raziskovalna vprašanja, ki jih lahko preveriš.
Podatke grafično prikaži tako, da si boš z grafi lahko pomagal pri preverjanju hipotez.
Grafično oceni, ali so porazdelitve podatkov po posameznih skupinah normalno porazdeljene.
Definirajmo osnovna raziskovalna vprašanja, ki jih lahko preverimo:
Ali obstaja statistično značilna razlika v času, ko se po zaužitju zdravila telesna temperatura zniža pod dovoljeno mejo glede na spol?
Ali obstaja statistično značilna razlika v času, ko se po zaužitju zdravila telesna temperatura zniža pod dovoljeno mejo glede na starostno skupino?
Ali obstaja statistično značilna razlika v času, ko se po zaužitju zdravila telesna temperatura zniža pod dovoljeno mejo glede na spol in starostno skupino?
Podatke moramo grafično prikazati tako, da bomo na podlagi grafov lahko preverjali hipoteze izpeljane iz zastavljenih raziskovalnih vprašanj.
Najprej naložimo podatke vaje iz pog. 1.1 vaja1.1.omv v Jamovi:
Preverimo prvo raziskovalno vprašanje: Ali obstaja statistično značilna razlika v času, ko se po zaužitju zdravila telesna temperatura zniža pod dovoljeno mejo glede na spol?
To bomo preverili z grafom okvir z ročaji (ang. boxplot). V Jamovi izvedemo izris boxplot-a na naslednji način: Analyses -> Exploration -> Descriptives, kjer za Variables izberemo spremenljivko čas glede na spremenljivko spol (Split by). Potem pa v razdelku Plots označimo Box Plot:
V oknu Rezultati se izrišeta grafa okvirja z ročajema.
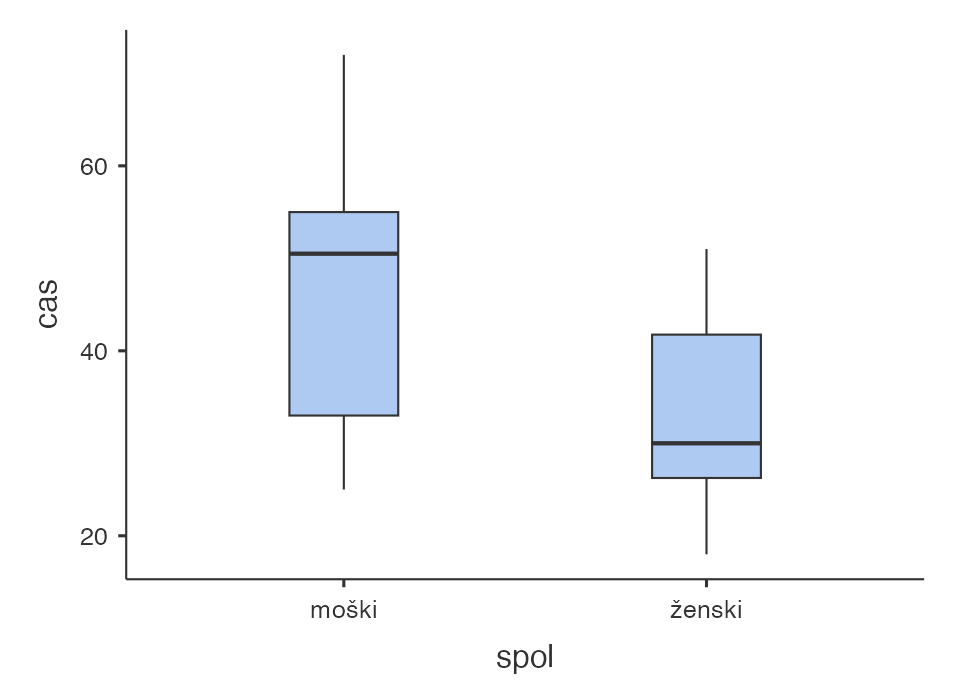
Grafa okvirja z ročajema prikazujeta porazdelitev meritev časa ločeno po spolu. Okvir grafa predstavlja meritve med 1. in 3. kvartilom, črta znotraj okvirja grafa predstavlja mediano meritev, ročaji grafa pa so dolgi 1.5 medkvartilne razdalje navzdol oziroma navzgor od mediane. Iz dobljenih grafov lahko ugotovimo, da grafa nista simetrična glede na neenako razdaljo med mediano ter 1. kvartilom in mediano ter 3. kvartilom, zato na podlagi tega lahko sklepamo, da verjetno meritve časa niso normalno porazdeljene. Mediana enega grafa leži zunaj intervala med 1. in 3. kvartilom drugega grafa, zato lahko potrdimo, da obstaja statistično značilna razlika v času med spoloma.
Preverimo drugo raziskovalno vprašanje: Ali obstaja statistično značilna razlika v času, ko se po zaužitju zdravila telesna temperatura zniža pod dovoljeno mejo glede na starostno skupino?
Narišimo graf okvir z ročaji oziroma boxplot z ukazom Analyses -> Exploration -> Descriptives, kjer za Variables izberemo spremenljivko čas glede na spremenljivko starostna skupina (Split by). Potem pa v razdelku Plots označimo Box Plot:
Izriše se naslednji graf:
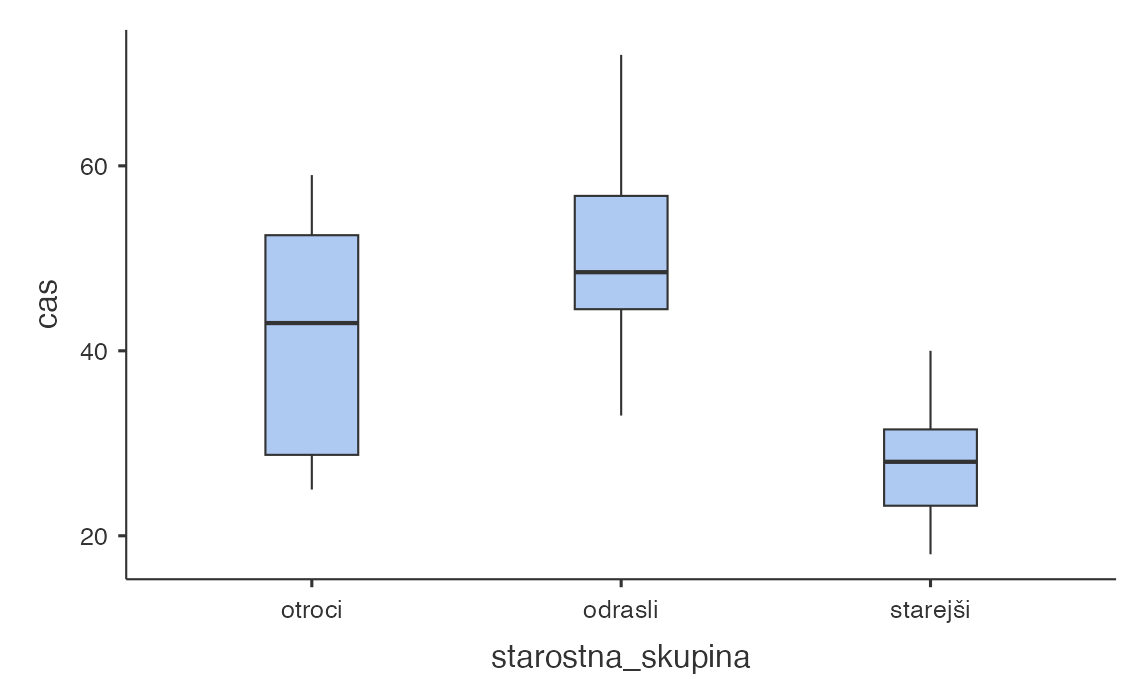
Na podlagi grafa okvir z ročaji ugotovimo, da skupina starejših izrazito odstopa od skupine odraslih in skupine otrok, saj mediana grafa skupine starejših ne seka območja znotraj 1. in 3. kvartila grafov skupine odraslih in skupine otrok. Skupina starejših je zato statistično značilno različna od skupine odraslih in od skupine otrok. Med skupino odraslih in skupino otrok pa ne moremo z gotovostjo trditi, da gre za statistično značilne razlike med njimi.
Preverimo tretje raziskovalno vprašanje: Ali obstaja statistično značilna razlika v času, ko se po zaužitju zdravila telesna temperatura zniža pod dovoljeno mejo glede na spol in starostno skupino?
Spet narišemo graf okvir z ročaji Analyses -> Exploration -> Descriptives, kjer za Variables izberemo spremenljivko čas glede na spremenljivko starostna skupina in spol (Split by). Potem pa v razdelku Plots označimo Box Plot:
Sedaj imamo drugačni izris, saj imamo 2 faktorja - starostno skupino in spol, zato dobimo boxplot različnih barv.
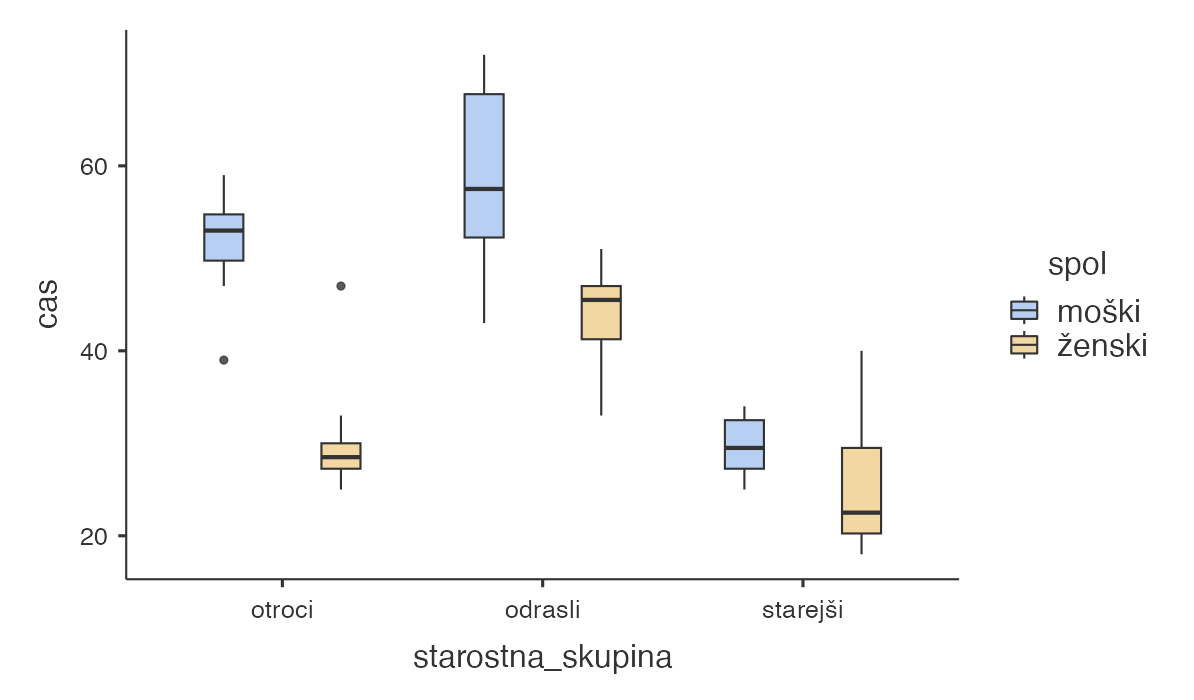
Ugotovimo, da se moški in ženske v starostni skupini otrok med seboj izrazito statistično značilno razlikujejo. Tudi v starostni skupini odraslih se moški in ženske razlikujejo, vendar nekoliko manj kot pri otrocih, še manj pa se razlikujejo moški in ženske glede na čas v starostni skupini starejših.
Pri primerjavi moških skupine otrok s skupino odraslih ugotovimo, da ni statistično značilnih razlik, medtem ko med moškimi skupine otrok in starejših ter odraslih in starejših statistično značilne razlike so.
Pri primerjavi žensk vseh treh starostnih skupin ugotovimo, da med skupino otrok in starejših ne obstajajo statistično značilne razlike, med skupino odraslih in starejših pa obstajajo statistično značilne razlike, prav tako pa tudi med skupino otrok in odraslih.
V skupini otrok vidimo še dve odstopajoči meritvi.
Grafična ocena, ali so podatki normalno porazdeljeni
Da lahko grafično ocenimo, ali so porazdelitve podatkov po posameznih skupinah normalno porazdeljene, bomo narisali graf kvartil-kvartil ali QQplot.
To naredimo na podoben način kot prej pri izrisu grafov okvir z ročajem, le da izberemo drugi graf za izris.
V primeru porazdelitev spremenljivke čas glede na spol izvedemo: Analyses -> Exploration -> Descriptives, kjer za Variables izberemo spremenljivko čas glede na spremenljivko spol (Split by). Potem pa v razdelku Plots označimo Q-Q Plots:
V oknu Rezultatov se nam izrišejo kvartil-kvartil grafi, ki so prikazani spodaj.
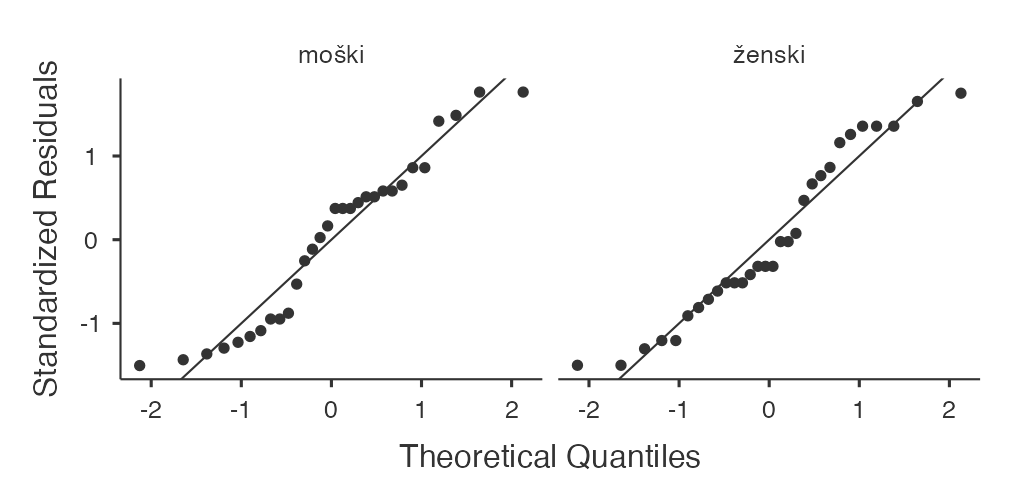
Subjektivno ocenimo, da podatki skupine moški niso normalno porazdeljeni, saj se podatki ne prilegajo premici kvartil-kvartil grafa, ampak od nje odstopajo z značilnim vzorcem v obliki črke S. Bolj kot podatki odstopajo od premice kvartil-kvartil, z večjo verjetnostjo lahko trdimo, da podatki niso normalno porazdeljeni.
Tudi pri skupini žensk po subjektivnem mnenju ugotovimo, da podatki niso normalno porazdeljeni. Vendar je odstopanje manjše kot v primeru moških. Zato lahko zaključimo, da je večja verjetnost, da so meritve časa v ženski skupini normalno porazdeljene kot pri moških.
Poglejmo še kvartil-kvartil grafe ločene po starostni skupini. Za izris grafov izvedemo: Analyses -> Exploration -> Descriptives, kjer za Variables izberemo spremenljivko čas glede na spremenljivko starostna skupina (Split by). Potem pa v razdelku Plots označimo Q-Q Plots:
Dobimo naslednje kvartil-kvartil grafe:
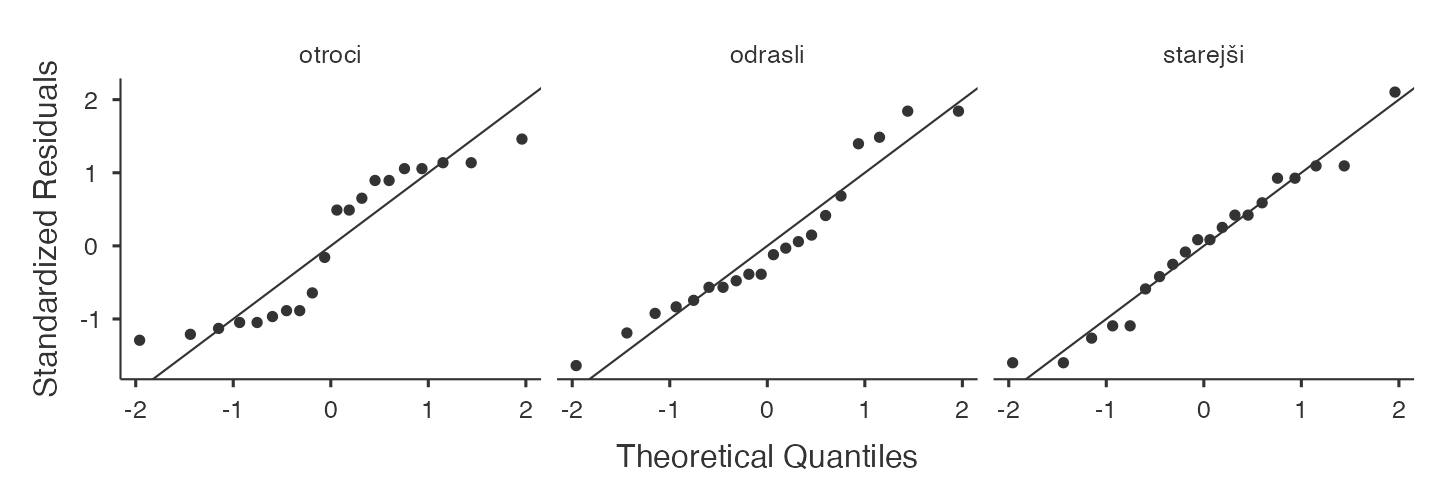
Tukaj lahko z gotovostjo trdimo, da podatki starostne skupine otrok niso normalno porazdeljeni, saj vidimo velika odstopanja od premice kvartil-kvartil grafa in značilni vzorec v obliki črke S. Podobno lahko ugotovimo tudi pri meritvah časa pri starostni skupini odraslih, medtem ko so odstopanja pri skupini starejših manjša, kar pomeni večjo verjetnost, da so te meritve normalno porazdeljene.
Glede na vse tri kvartil-kvartil grafe glede na starostno skupino lahko trdimo, da je večja verjetnost, da so meritve časa starostne skupine starejših normalno porazdeljene, medtem ko je verjetnost, da so meritve starostne skupine otroci in odrasli normalno porazdeljene, manjša.
Graf okvir z ročaji (ang. boxplot) je graf, ki nam prikaže obliko porazdelitve skalarnih spremenljivk. Okvir grafa predstavlja meritve med 1. in 3. kvartilom, črta znotraj okvirja grafa predstavlja mediano meritev, ročaji grafa pa so dolgi 1.5 medkvartilne razdalje navzdol oziroma navzgor od mediane. Meritve izven ročajev so prikazane posebej in jih štejemo med odstopajoče točke (ang. outliers). Če mediana grafa ene skupine meritev ne seka območja znotraj 1. in 3. kvartila grafa druge skupine meritev, lahko trdimo, da med skupinama obstajajo statistično značilne razlike v opazovani spremenljivki.
Z grafom kvartil-kvartil (ang. QQplot) preverjamo, ali so meritve normalno porazdeljene. V primeru normalno porazdeljenih meritev bodo meritve ležale na premici kvartil-kvartil, sicer bodo od nje odstopale. Premica kvartil-kvartil povezuje točki, ki predstavljata par 1. kvartil dejanskih meritev in pričakovani 1. kvartil v primeru normalne porazdelitve ter 3. kvartil dejanskih meritev in pričakovani 3. kvartil v primeru normalne porazdelitve.
1.3 Statistike za ugotavljanje oblike porazdelitve podatkov
V datoteki kreatinin_akin_pacienti.xlsx so podatki o pacientih, ki smo jim merili kreatinin pred in po operaciji, da smo ugotavljali, kateri pacienti imajo okvaro ledvične funkcije (Kališnik et al. 2017).
Pri teh pacientih nas zanimajo podatki o starosti:
Izvedi frekvenčno analizo pacientov po starosti.
Izračunaj povprečje, mediano in najpogostejšo meritev ter komentiraj te vrednosti. Zakaj so razlike med temi merami?
Izračunaj še 25., 50. in 75. percentil in komentiraj te vrednosti.
Kaj lahko poveš o porazdelitvi teh podatkov?
Uvozimo podatke iz Excel datoteke v Jamovi. Izberemo datoteko kreatinin_akin_pacienti.xlsx. Jamovi lahko bere datoteke iz Excela in SPSS.
Tako uvozimo podatke o pacientih v Jamovi:
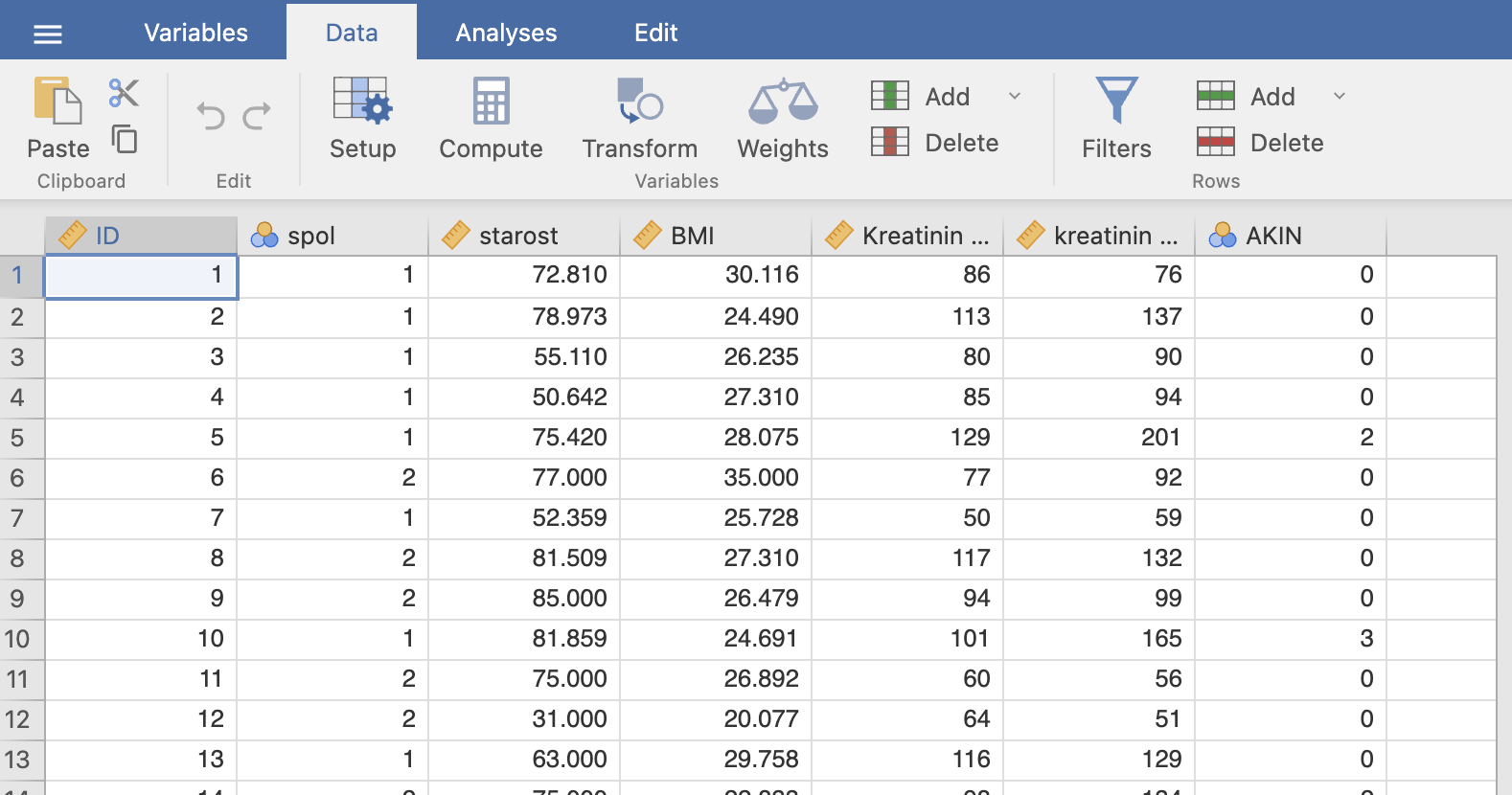
V teh podatkih nas zanimajo samo podatki o starosti, zato bomo v nadaljevanju delali s temi podatki.
Če hočemo podati frekvenčno analizo meritev starosti, bomo spremenljivko starost razdelili na starostne intervale po 10 let. To bomo naredili tako, da bomo uvedli novo spremenljivko starostne skupine, kjer bodo kategorije predstavljale starostne skupine po 10 let (od 21 do 30 let, od 31 do 40 let, od 41 do 50 let, ipd.). To naredimo tako z ukazom Data -> Transform, pri čemer ustvarimo novo spremenljivko starostne skupine, pod Source variable pa izberemo spremenljivko starost.
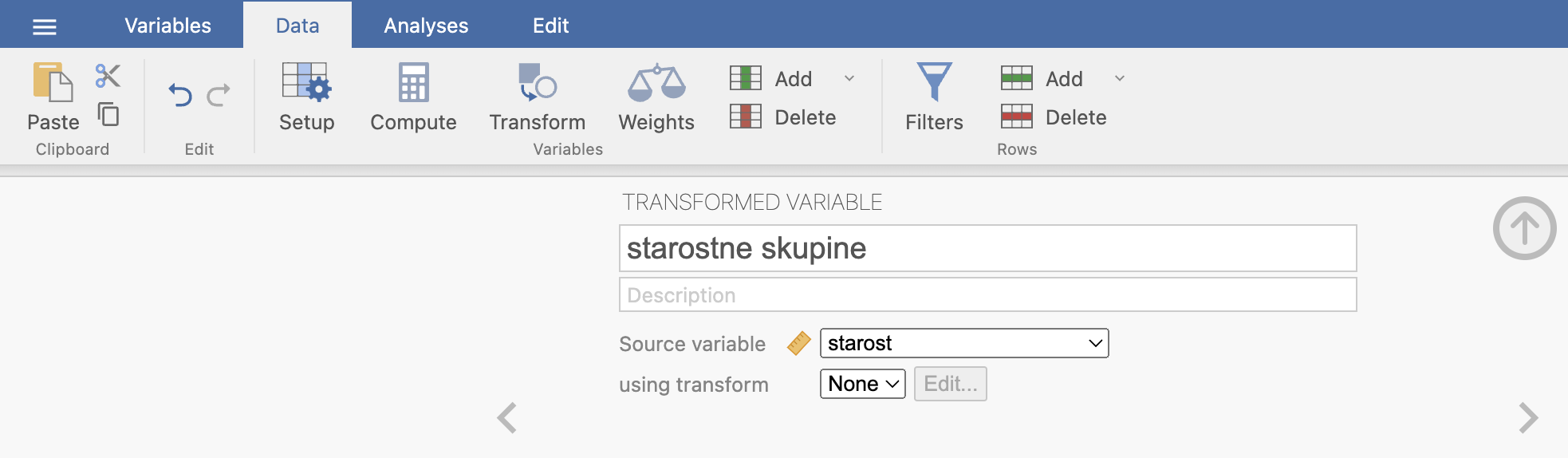
Novo transformacijo definiramo z using transform -> Create New Transform … in jo z gumbom Add recode condition izpolnimo na naslednji način:
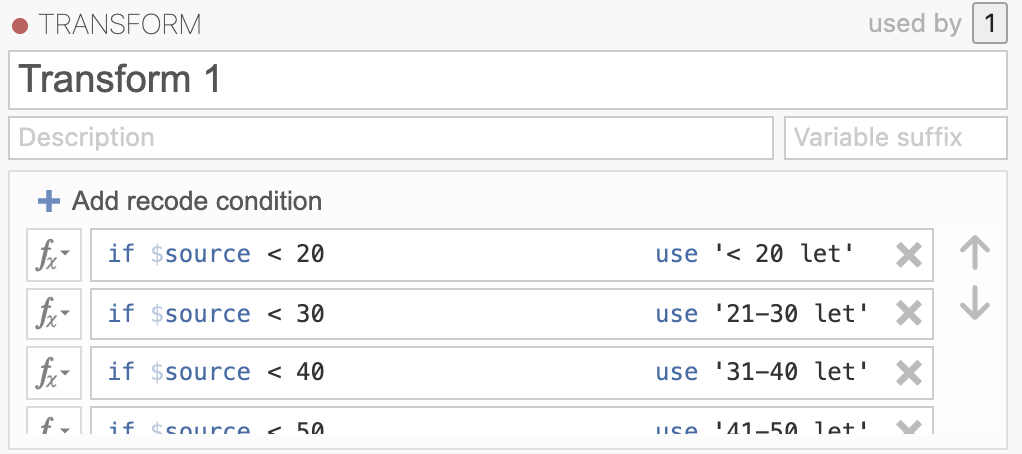
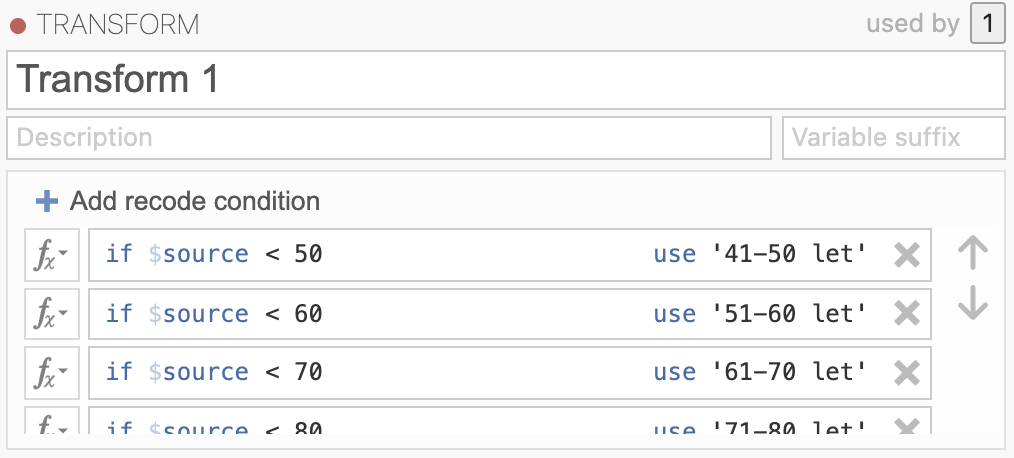
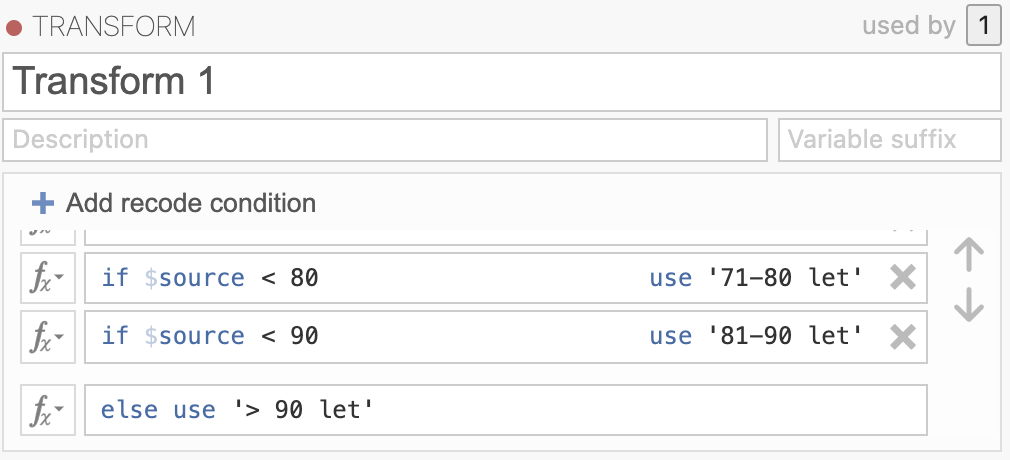
Tako dobimo novo kategorijsko spremenljivko starostne skupine, kjer imamo kategorije < 20 let, 21-30 let, 31-40 let, 41-50 let, 51-60 let, 61-70 let, 71-80 let, 81-90 let, > 90 let.
Za izvedbo frekvenčne analize pacientov po starosti izberemo Analyses -> Exploration -> Descriptives, kjer za Variables izberemo spremenljivko starostne skupine in označimo Frequency Tables.
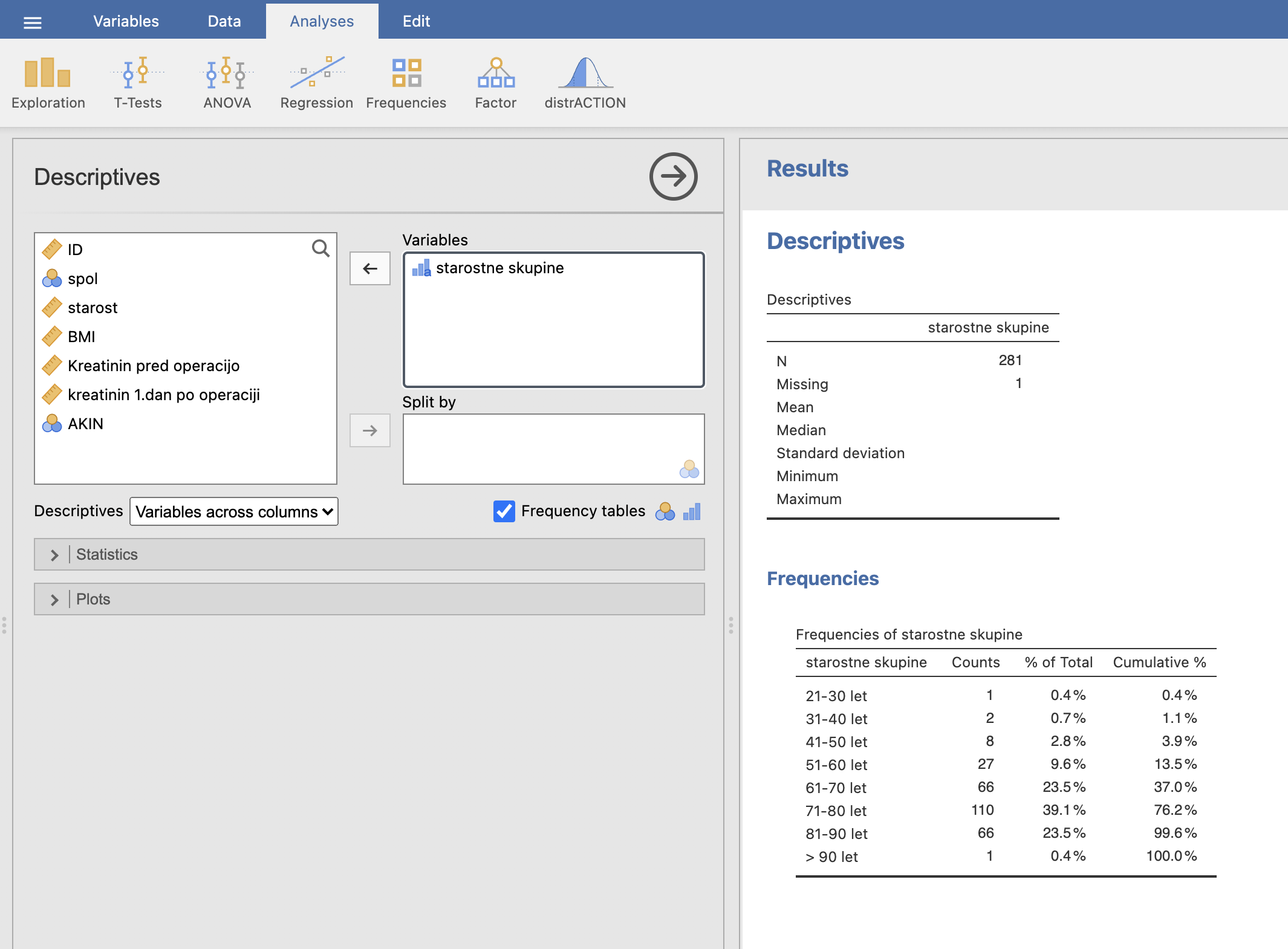
Iz frekvenčne tabele na desni strani lahko razberemo, koliko ljudi spada v določen starostni razred. Ugotovimo, da je največ pacientov starih med 71 in 80 let.
Podatke starostne skupine lahko tudi izrišemo, če v razdelku Plots izberemo Bar Plot.
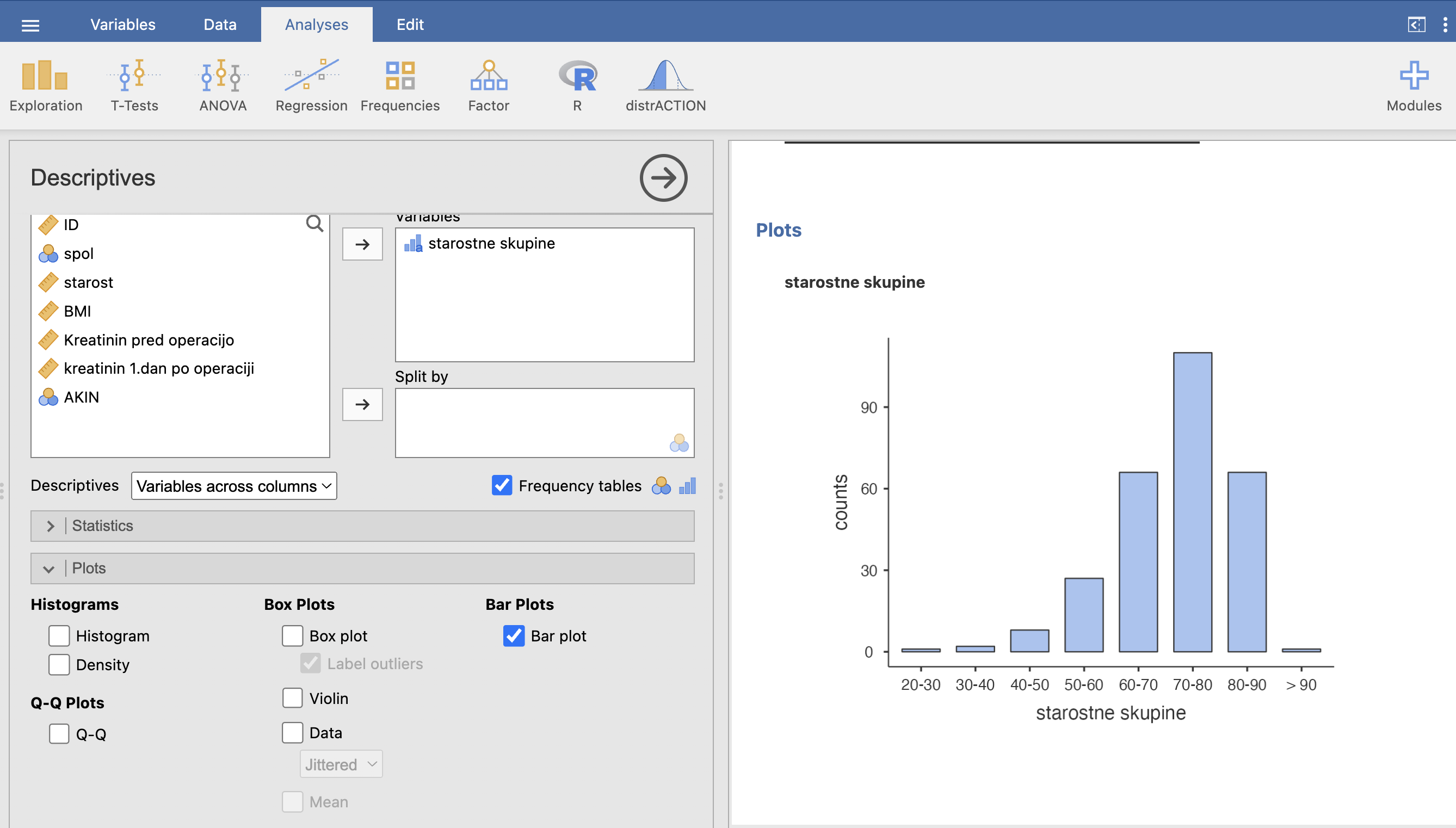
Iz frekvenčne tabele in stolpičnega diagrama lahko vidimo, da so podatki starosti nesimetrično porazdeljeni. Več imamo starejših pacientov kot mlajših, kar je pogosto pri analizi podatkov v zdravstvu.
Izračunajmo še statistike, ki jih uporabljamo za ugotavljanje oblike porazdelitve podatkov in jih lahko poročamo v takšnih primerih. To bomo sedaj delali neposredno na skalarni spremenljivki starost. Izračunali bomo mere središčnosti: povprečje, mediano in najbolj pogosto meritev ter 25., 50. in 75. percentil. To izvedemo z Analyses -> Exploration -> Descriptives, kjer za Variables izberemo spremenljivko starost in v razdelku Statistics označimo Mean, Median, Mode in Percentiles.
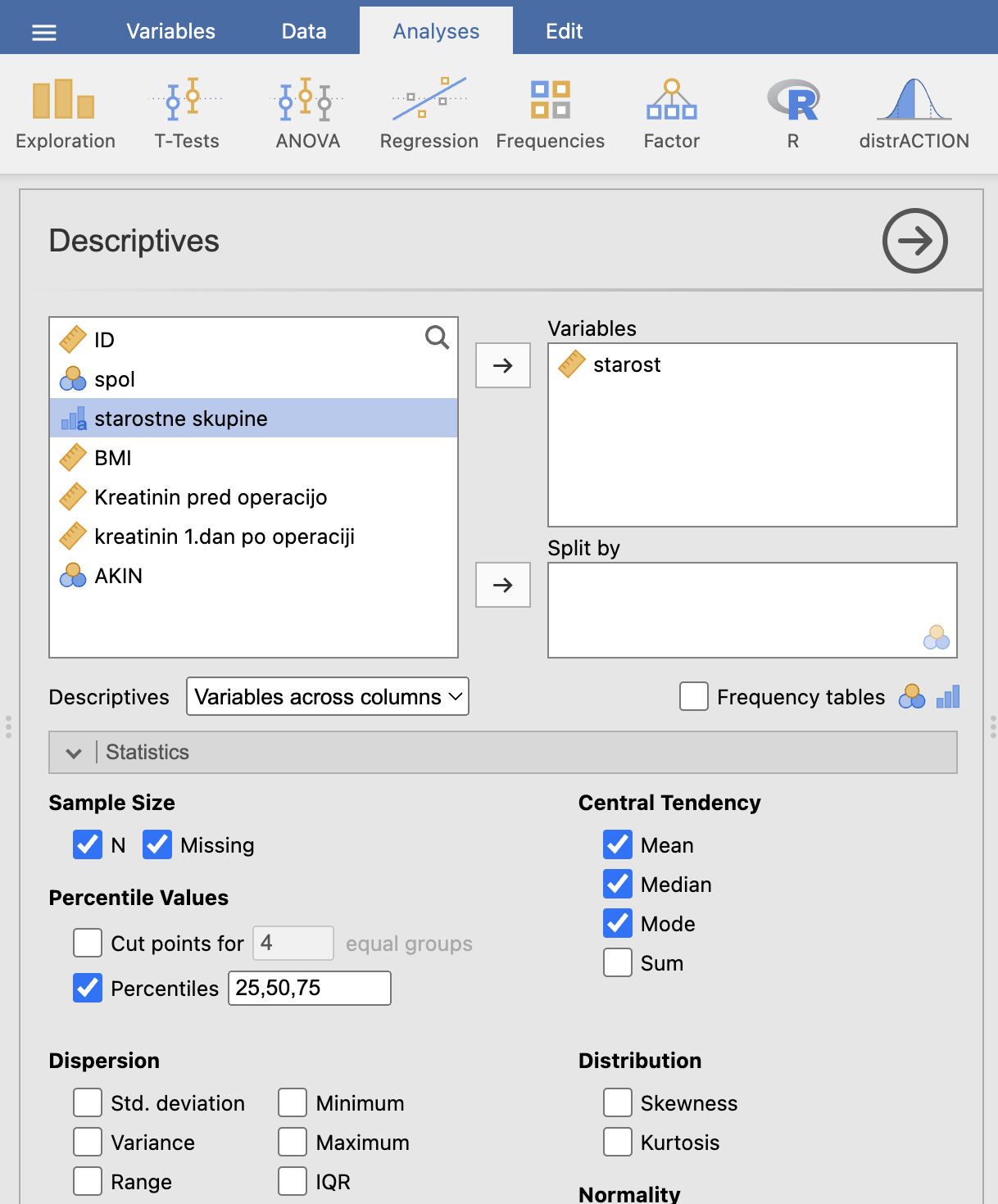
V oknu z rezultati dobimo naslednjo tabelo:
Iz rezultatov razberemo, da je povprečje enako 71.6 let, mediana 74 let in najpogostejša meritev 77 let. Opazimo, da so te vrednosti različne med seboj, kar je posledica nesimetrične porazdelitve podatkov. V primeru simetričnih porazdelitev so te vrednosti enake.
Da je porazdelitev nesimetrična lahko sklepamo tudi glede na razlike med vrednostmi posameznih percentilov. Porazdelitev meritev je raztegnjena v levo in strmo padajoča v desno.
Pri tej vaji smo se ukvarjali z obliko porazdelitve meritev. Ugotovili smo, da če je porazdelitev podatkov nesimetrična, potem so srednje vrednosti (povprečje, mediana in najpogostejša vrednost) različne. Če so te vrednosti enake, pomeni da je porazdelitev podatkov simetrična.
Podatek o obliki porazdeljenosti podatkov nam prikažejo tudi razlike med percentili. Če so te razlike enake, je porazdelitev simetrična, če so razlike neenakomerne je porazdelitev podatkov nesimetrična.
V našem primeru srednje vrednosti in razlike med percentili pri spremenljivki starost kažejo na nesimetričnost podatkov. V takem primeru je za mero središčnosti bolj smiselno poročati mediano ter 1. in 3. kvartil (25. in 75. percentil).
1.4 Delo s porazdelitvami – normalna porazdelitev
Merimo doze na 100 pacientih in ugotovimo, da so doze normalno porazdeljene s povprečjem 7 enot in standardnim odklonom 1.5.
Kakšna je verjetnost, da bo doza na pacienta večja od 9 enot?
Kakšna je verjetnost, da bo doza med 6 in 8 enotami?
Kakšna je doza, ki je presežena v 90 % meritev?
Kakšna je pričakovana vrednost 1. in 3. kvartila naših meritev in koliko znaša medkvartilna razdalja?
Na katerem intervalu se nahaja 95 % vseh meritev?
Kakšen bi moral biti standardni odklon, da bi lahko trdili, da bo v 99 % primerov doza manjša od 8 enot?
V programu Jamovi najprej dodamo nov modul v program z ukazom +Modules, kjer izberemo jamovi library:
 V knjižnici modulov poiščemo modul distrACTION in ga namestimo v program:
V knjižnici modulov poiščemo modul distrACTION in ga namestimo v program:

Po namestitvi se nam nov modul pokaže v orodni vrstici programa Jamovi:

Kakšna je verjetnost, da bo doza na pacienta večja od 9 enot?
Za izračun željene verjetnosti bomo uporabili funkcijo CDF, ki je definirana kot \(CDF(x1) = P(x \le x1)\). V našem primeru moramo izračunati \(p = 1- CDF(9) = P(x > 9)\) pri normalno porazdeljeni spremenljivki \(x\). To se z uporabo modula distrACTION v Jamovi izvede z distrACTION -> Normal Distribution.
V levem oknu izberemo ustrezne parametre normalne porazdelitve, torej povprečje 7 in standardni odklon (SD) 1.5 ter izračunamo verjetnost Compute probability z izbiro \(P(X \ge x1)\). V desnem oknu pa dobimo rezultate izračuna in sicer verjetnost 0.091 in izris, katero verjetnost smo izračunali na podlagi normalne porazdelitve z našimi parametri.
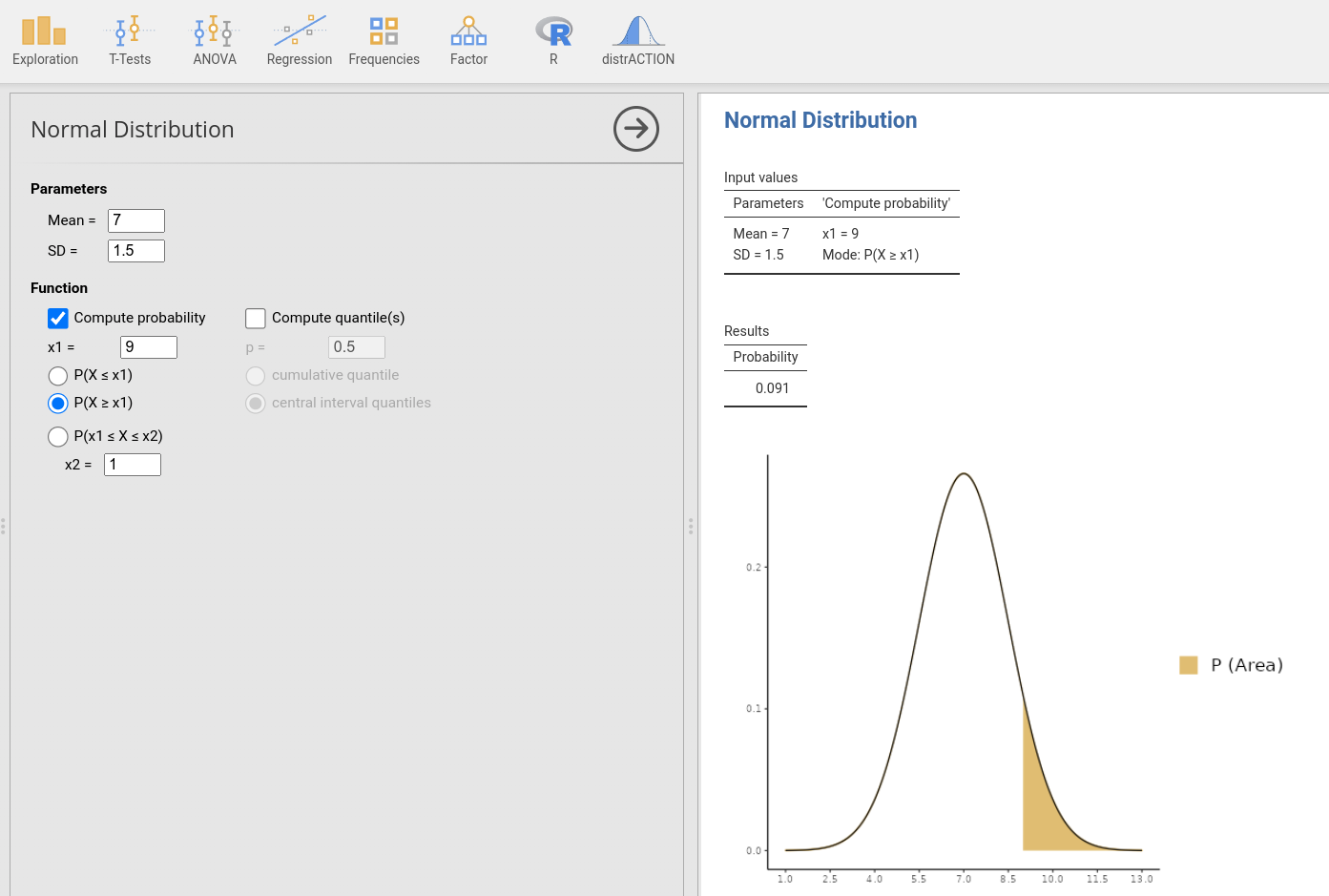
Rešitev 0.091 predstavlja verjetnost, da bo doza na pacienta višja od 9 enot oziroma, da imamo 9 % verjetnost, da dobi pacient dozo višjo od 9 enot.
Kakšna je verjetnost, da bo doza med 6 in 8 enotami?
Ker iščemo verjetnost, da bo doza na pacienta med 6 in 8 enotami, je potrebno izračunati verjetnost z distrACTION -> Normal Distribution.
V levem oknu izberemo ustrezne parametre normalne porazdelitve, torej povprečje 7 in standardni odklon (SD) 1.5 ter izračunamo verjetnost Compute probability z izbiro \(P(x1 \le X \le x2)\), kjer za \(x1\) izberemo spodnjo mejo, torej \(x1=6\) in za \(x2\) zgornjo mejo, torej \(x2=8\).
V desnem oknu pa dobimo rezultate izračuna in sicer verjetnost 0.495 in izris, katero verjetnost smo izračunali na podlagi normalne porazdelitve z našimi parametri.
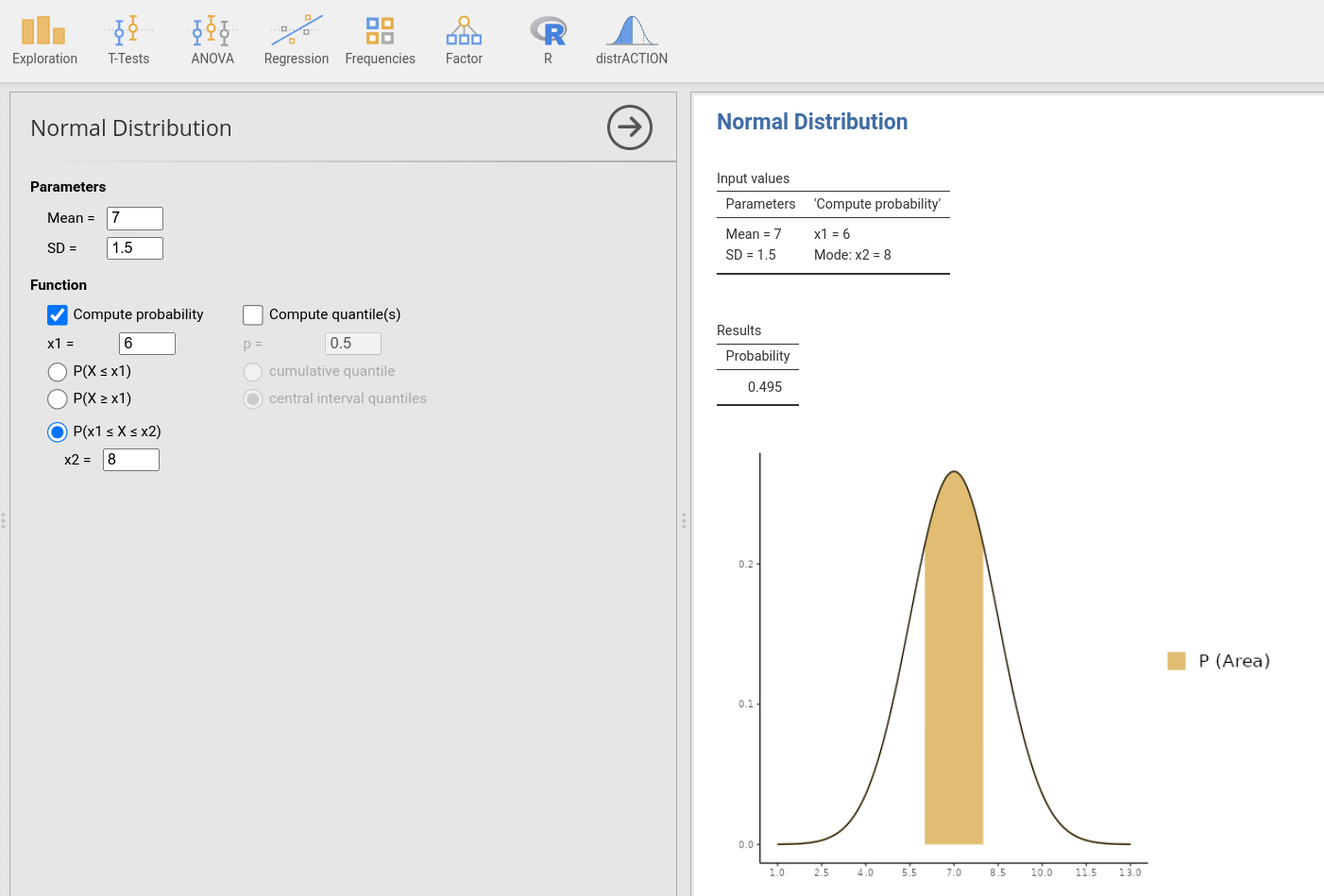
Rešitev 0.495 predstavlja verjetnost, da bo doza na pacienta med 6 in 8 enotami, oziroma da bodo pacienti prejeli dozo med 6 in 8 enotami v 49.5 % primerov.
Kakšna je doza, ki je presežena v 90 % meritev?
Za izračun iskane vrednosti bomo uporabili funkcijo IDF, ki je inverzna funkcija CDF. IDF je mejna vrednost meritve x, pri kateri je \(CDF(x) = p\).
Zanima nas, pri kateri vrednosti je CDF enak 0.1. Torej katera je tista vrednost doze (M), ki jo preseže 90 % pacientov. Poiskati moramo rešitev za M, da bo \(CDF(M) = 0.1\) z distrACTION -> Normal Distribution.
V levem oknu izberemo ustrezne parametre normalne porazdelitve, torej povprečje 7 in standardni odklon (SD) 1.5 ter izračunamo vrednost Compute quantile(s) z izbiro \(p = 0.1\) in izbiro cumulative quantile. V desnem oknu dobimo rezultate izračuna in sicer vrednost doze 5.08 in izris, katero vrednost smo izračunali na podlagi normalne porazdelitve z našimi parametri.
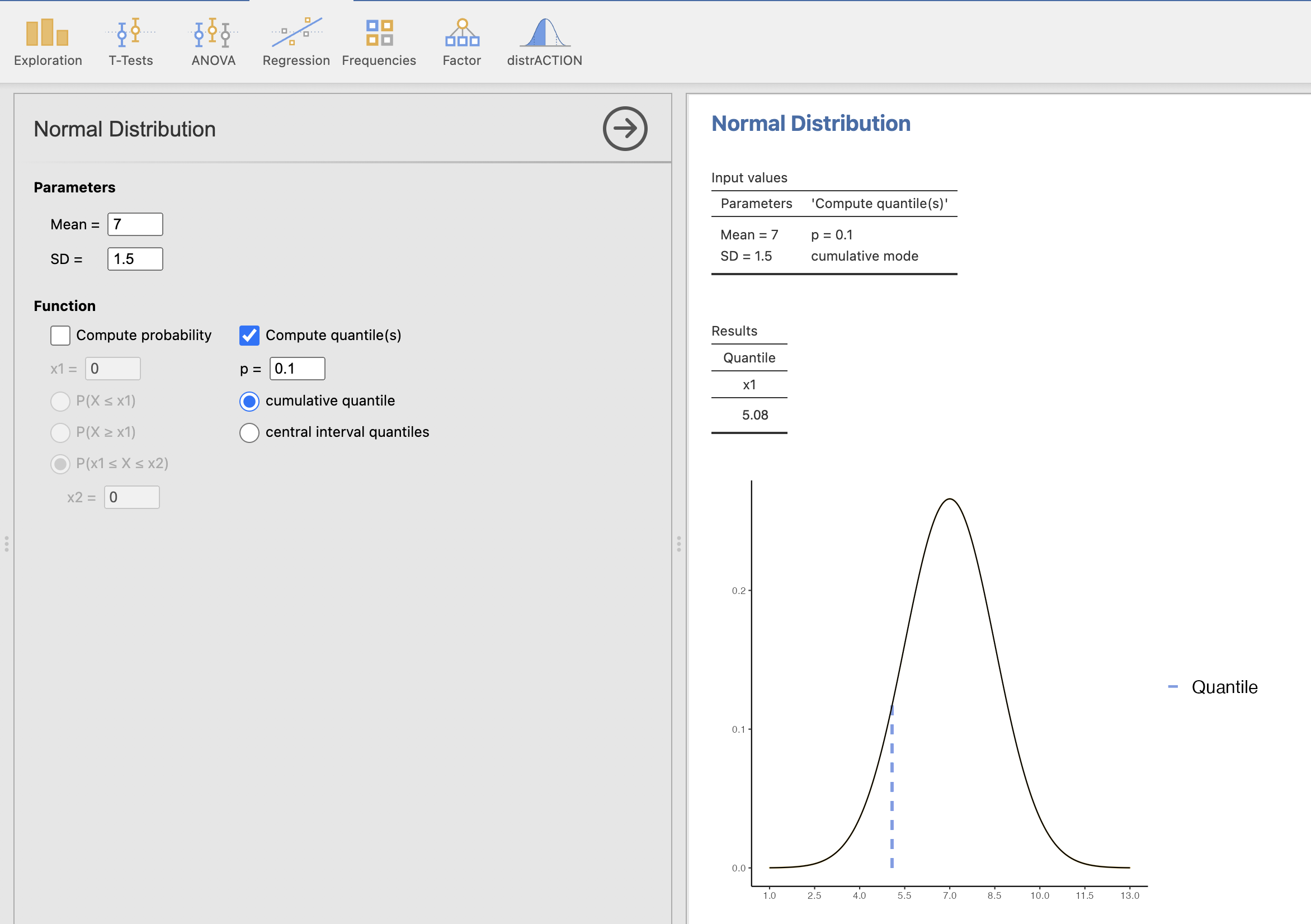
Vrednost doze, ki je presežena v 90 % meritev je 5,08 enot.
Kakšna je pričakovana vrednost 1. in 3. kvartila naših meritev in koliko znaša medkvartilna razdalja?
Medkvartilna razdalja je razdalja med 1. in 3. kvartilom. Izračunamo jo tako, da od vrednosti 3. kvartila odštejemo vrednost 1. kvartila.
Vrednost 1. kvartila izračunamo z \(IDF(0.25)\), vrednost 3. kvartila pa z \(IDF(0.75)\). Medkvartilna razdalja je \(IDF(0.75) - IDF(0.25)\). Zanima nas, pri kateri vrednosti je CDF enak 0.25 in pri kateri vrednosti je enak 0.75.
Najprej moramo poiskati rešitev za M1, da bo \(CDF(M1) = 0.25\) z distrACTION -> Normal Distribution.
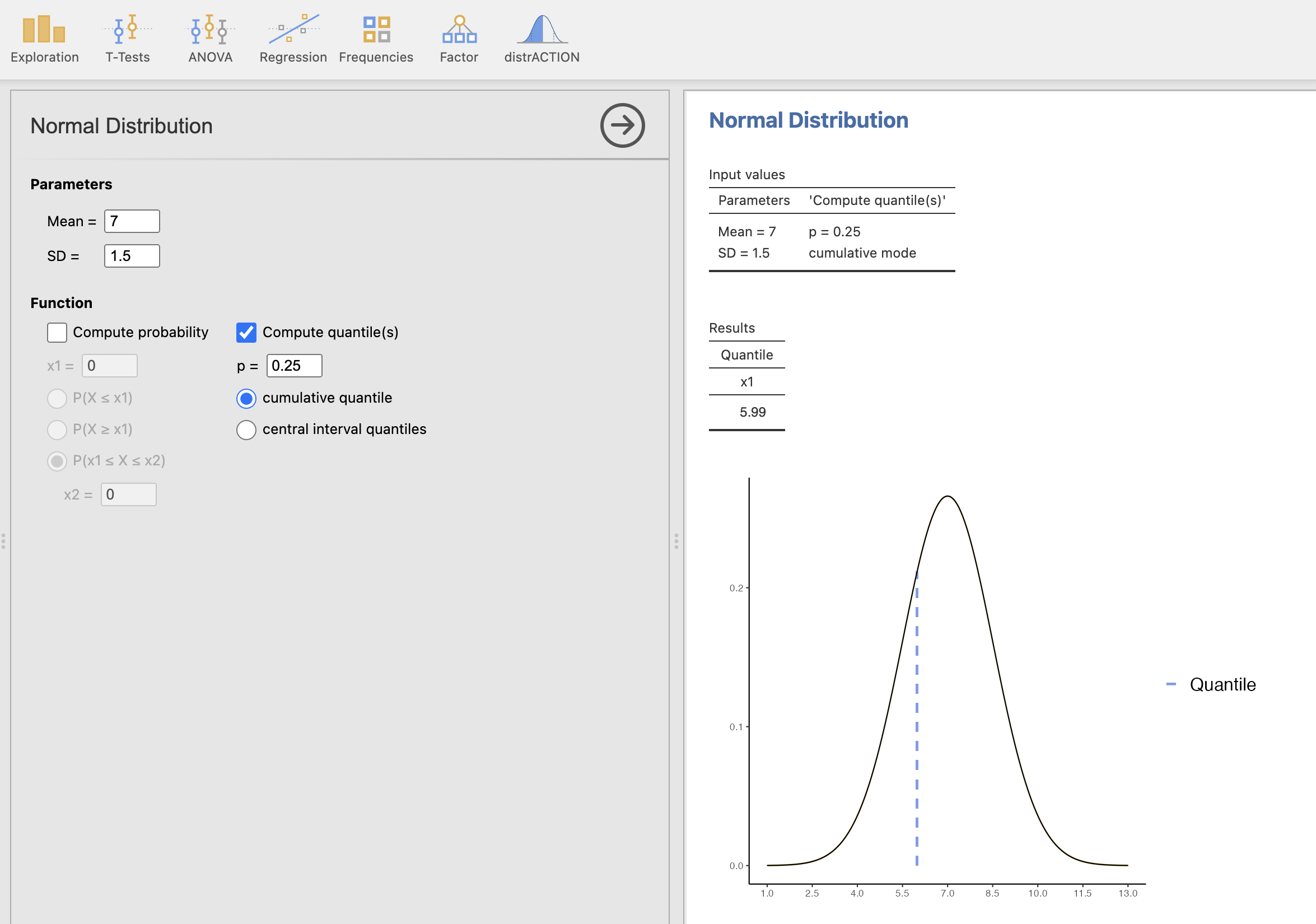
V levem oknu izberemo ustrezne parametre normalne porazdelitve, torej povprečje 7 in standardni odklon (SD) 1.5 ter izračunamo vrednost Compute quantile(s) z izbiro \(p = 0.25\) in izbiro cumulative quantile. V desnem oknu dobimo rezultate izračuna in sicer vrednost doze 5.99 in izris, katero vrednost smo izračunali na podlagi normalne porazdelitve z našimi parametri.
Poiščimo še rešitev za M2, da bo \(CDF(M2) = 0.75\) z distrACTION -> Normal Distribution.
V levem oknu izberemo ustrezne parametre normalne porazdelitve, torej povprečje 7 in standardni odklon (SD) 1.5 ter izračunamo vrednost Compute quantile(s) z izbiro \(p = 0.75\) in izbiro cumulative quantile. V desnem oknu dobimo rezultate izračuna in sicer vrednost doze 8.01 in izris, katero vrednost smo izračunali na podlagi normalne porazdelitve z našimi parametri.
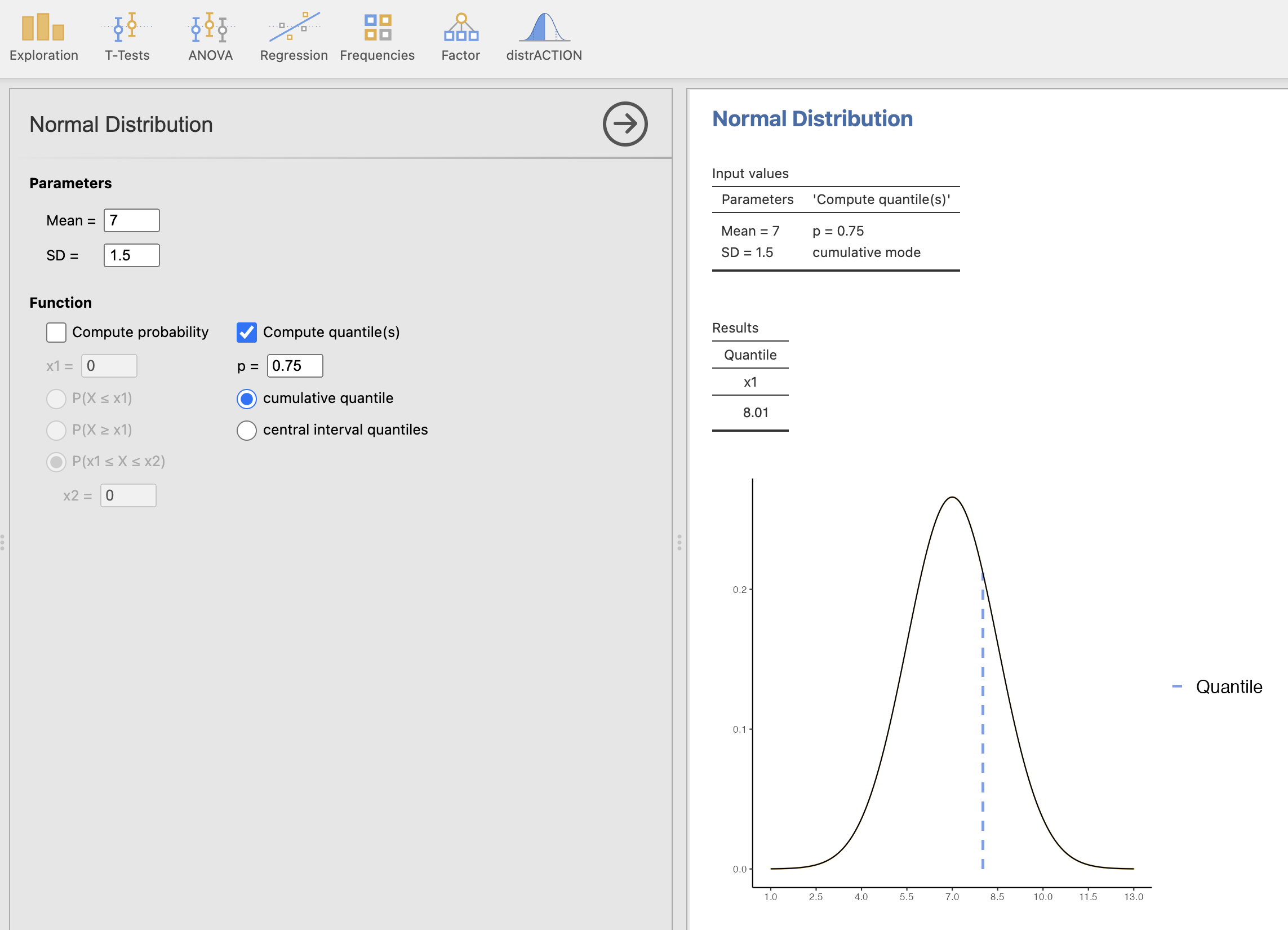
Medkvartilna razdalja (IQR) \(= IDF(0.75) - IDF(0.25) = 8.01 - 5.99 = 2.02\)
Na katerem intervalu se nahaja 95 % vseh meritev?
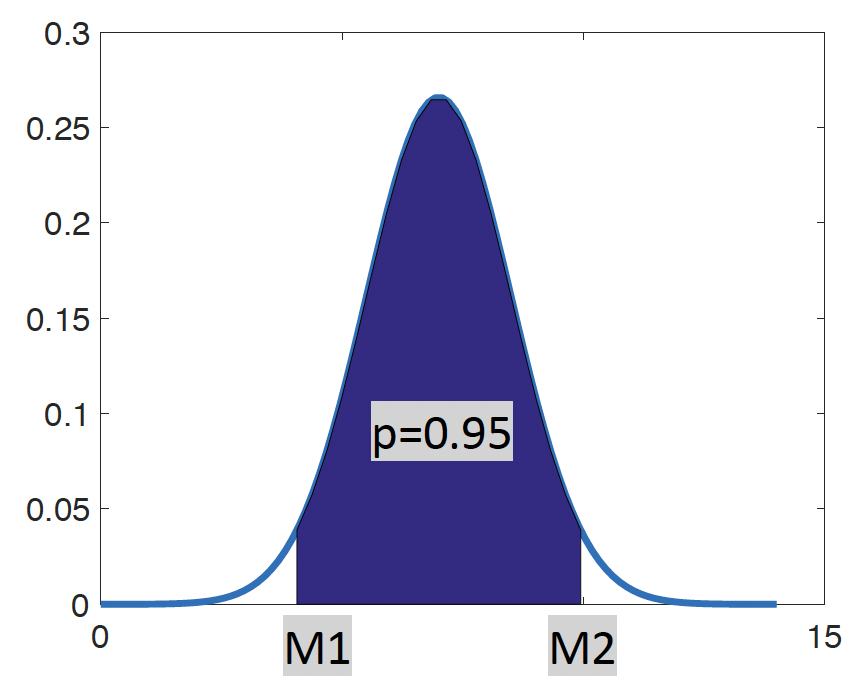
Vrednost M1 izračunamo z \(IDF(0.025),\) vrednost M2 pa z \(IDF(0.975)\).
Z ukazom distrACTION -> Normal Distribution najprej v levem oknu izberemo ustrezne parametre normalne porazdelitve, torej povprečje 7 in standardni odklon (SD) 1.5 ter izračunamo vrednost Compute quantile(s) z izbiro \(p = 0.025\) in izbiro cumulative quantile.
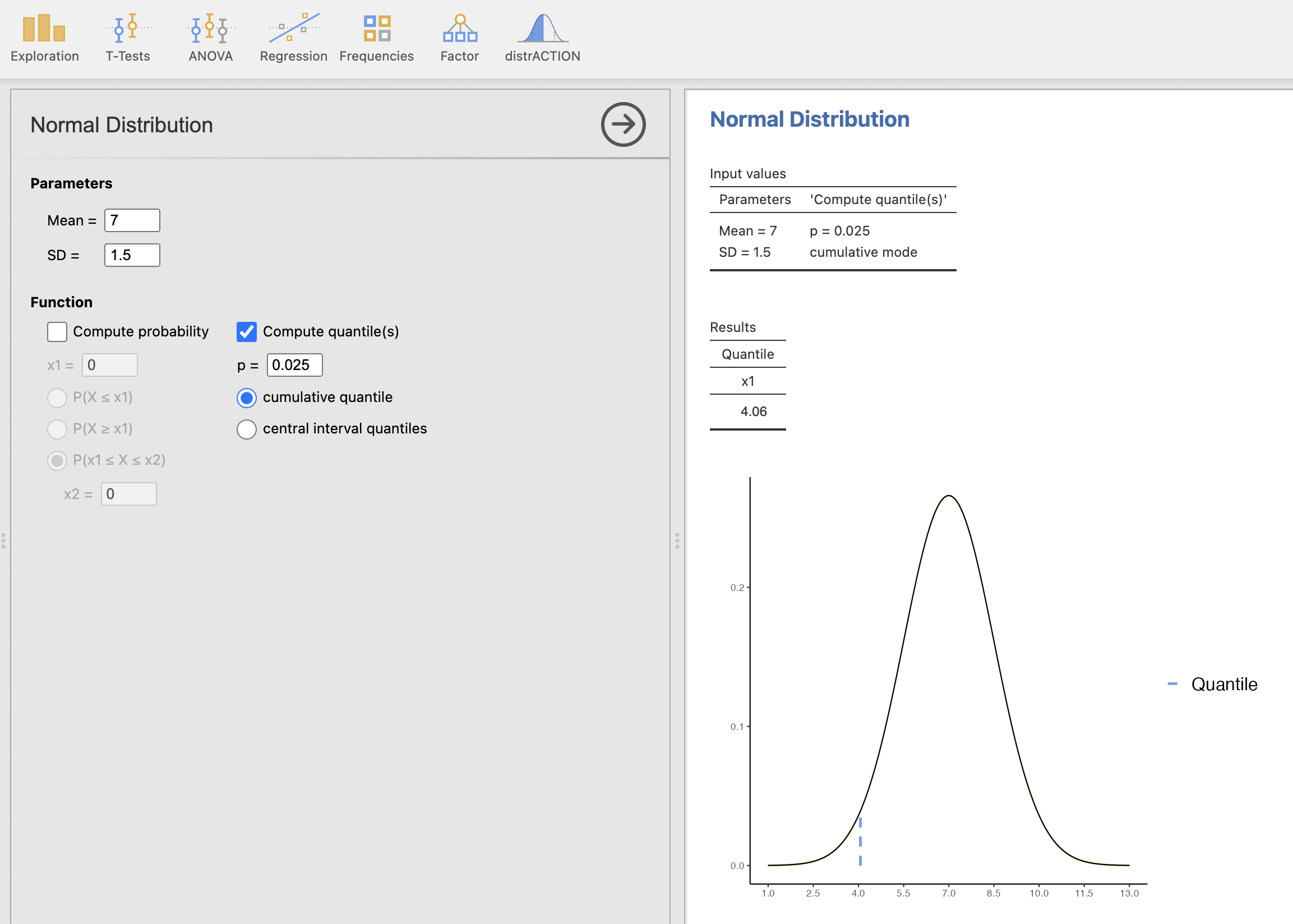
V desnem oknu dobimo rezultate izračuna in sicer vrednost doze M1 = 4.06 in izris, katero vrednost smo izračunali na podlagi normalne porazdelitve z našimi parametri.
Enak postopek ponovimo za \(p = 0.975\) za izračun M2:
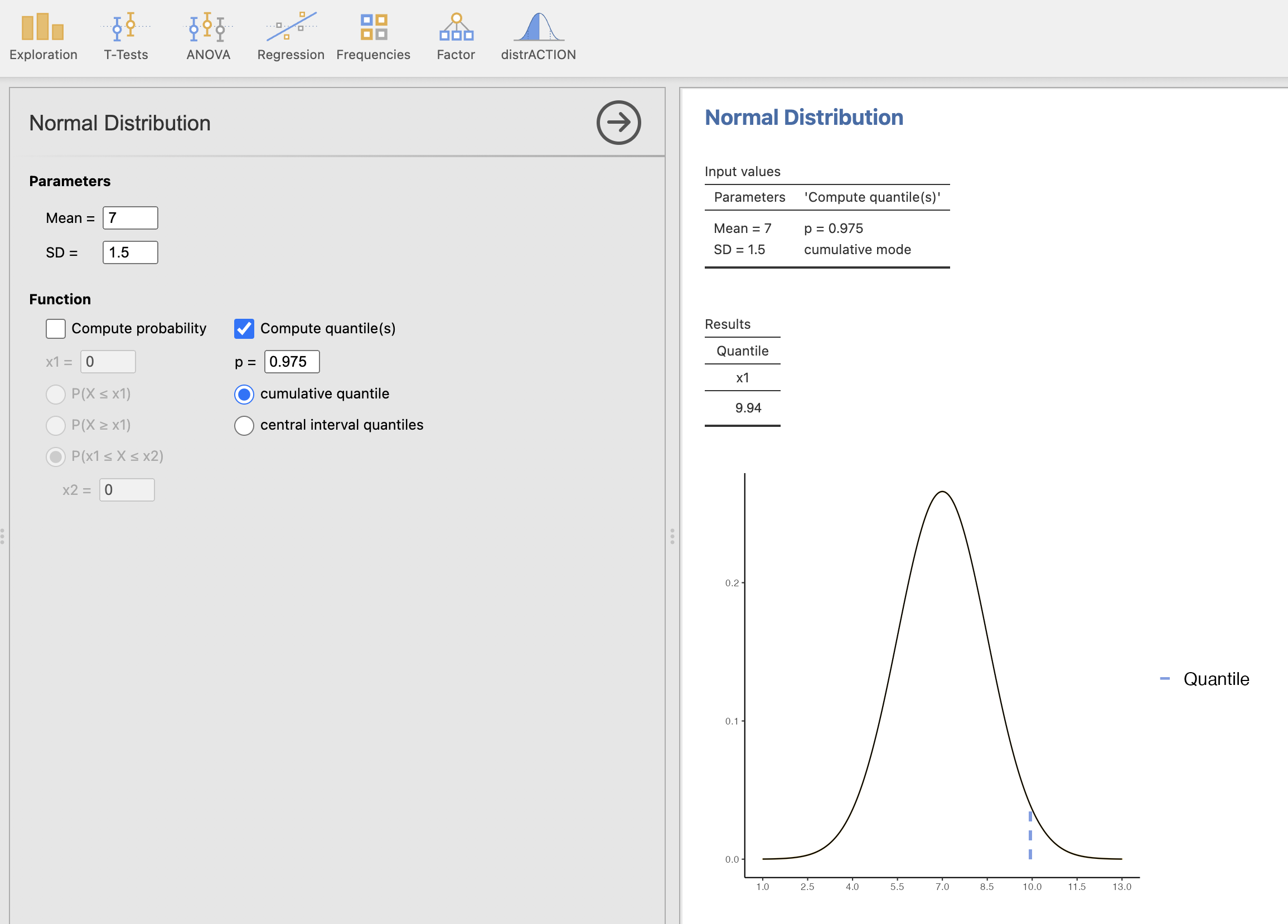
V desnem oknu dobimo rezultate izračuna M2 in sicer vrednost doze 9.94 in izris, katero vrednost smo izračunali na podlagi normalne porazdelitve z našimi parametri.
95 % vseh meritev se torej nahaja na intervalu med 4.06 in 9.94.
Kakšen bi moral biti standardni odklon, da bi lahko trdili, da bo v 99 % primerov doza manjša od 8 enot?
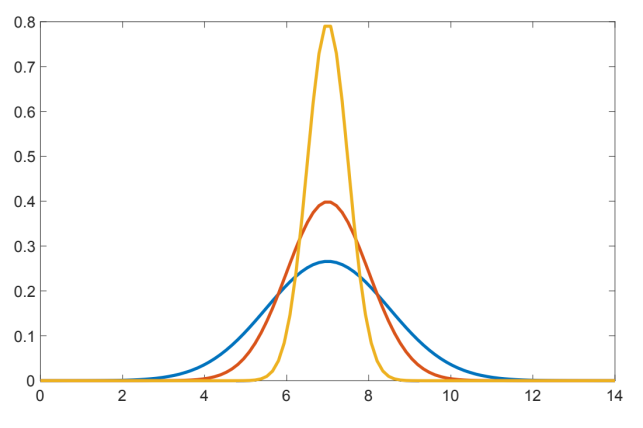
Spreminjati moramo standardni odklon normalne porazdelitve toliko časa, dokler ne bo \(CDF(8,7,s) = 0.99\). Pri tem se spreminja oblika normalne porazdelitve, kot je prikazano na sliki.
Uporabimo modul distrACTION v Jamovi in izvedemo ukaz distrACTION -> Normal Distribution.
V levem oknu izberemo ustrezne parametre normalne porazdelitve, torej povprečje 7 in manjši standardni odklon (SD) kot 1.5, saj želimo imeti manj razpršene podatke. Izračunamo verjetnost Compute probability pri x1 = 8 in izbiro \(P(X \le x1)\). Postopoma nižamo vrednost standardnega odklona in v desnem oknu z rezultati spremljamo izračune, ko verjetnost doseže vrednost 0.99. To se zgodi pri standardnem odklonu velikosti 0.4.
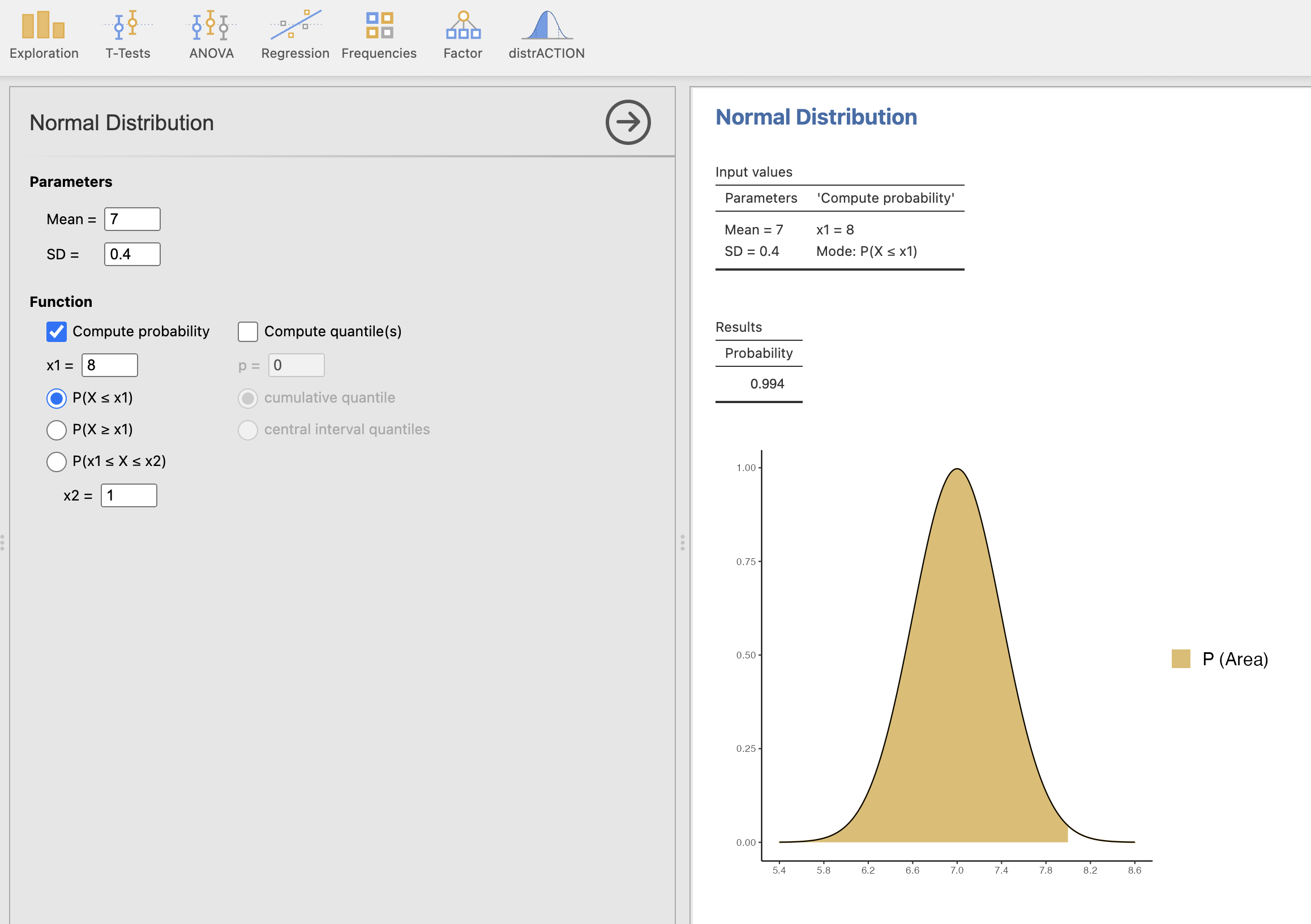
\(PDF(x)\) je funkcija porazdelitve verjetnosti meritev. Pove nam, kolikšna je verjetnost, da je meritev enaka x.
\(CDF(t)\) je kumulativna funkcija porazdelitve verjetnosti meritev. Pove nam, kolikšna je ploščina pod krivuljo \(PDF\) do točke \(t\). \(CDF(t)\) je naraščajoča funkcija in je lahko največ 1. Funkcijo \(CDF\) uporabljamo pri računanju verjetnosti, če poznamo porazdelitev podatkov.
\(IDF\) je inverzna funkcija funkcije \(CDF\). \(y=IDF(p)=CDF^{-1}(p)\). Pove nam, pri kakšni mejni vrednosti \(y\), dosežemo verjetnost \(p\).
Če poznamo porazdelitev verjetnosti meritev, lahko s temi funkcijami računamo različne verjetnosti in mejne vrednosti glede na verjetnosti v meritvah.
1.5 Delo s porazdelitvami – binomska porazdelitev
Verjetnost, da pacient umre pri infarktu je 0.04. Denimo, da imamo 10 pacientov, ki so doživeli infarkt.
Kakšna je verjetnost, da noben od pacientov ne bo umrl?
Kakšna je verjetnost, da bo 1 pacient umrl?
Kakšna je verjetnost, da bo polovica pacientov umrla?
V tem primeru imamo opravka z binomsko porazdelitvijo. To je porazdelitev verjetnosti, ko nas zanima, kakšna je verjetnost \(x\) izidov (v kakršnem koli vrstnem redu) v \(N\) dogodkih v primeru, ko je verjetnost enega izida \(p\). Porazdelitev računamo po naslednji formuli:
\[PDF(x) = \begin{pmatrix} N \\ x \end{pmatrix}p^{x}{(1 - p)}^{N - x},\]
kjer je \(x\) število izidov v \(N\) dogodkih, \(p\) je verjetnost enega izida, binomski simbol \(\small \begin{pmatrix} N \\ x \end{pmatrix}\) pa predstavlja število vseh kombinacij \(x\) izidov v \(N\) dogodkih. Primer binomske porazdelitve predstavlja met kovanca. Če se sprašujemo, kakšna je verjetnost, da vržemo 3 cifre v 10-ih metih kovanca ob verjetnosti, da vržemo cifro p = 0.5, to izračunamo na naslednji način:
\[PDF(3) = \begin{pmatrix} 10 \\ 3 \end{pmatrix}{0.5}^{3}{(1 - 0.5)}^{7} = 0.1172.\]
Razlaga zgornjega izračuna je naslednja. Število kombinacij, da vržemo 3 cifre v 10-ih metih, izračunamo z \(\small \begin{pmatrix} 10 \\ 3 \end{pmatrix}\), verjetnost, da vržemo 3 cifre je \({0.5}^{3}\), verjetnost, da vržemo preostalih 7 grbov pa \({(1 - 0.5)}^{7}\). Vrednost 0.1172 je verjetnost, da vržemo 3 cifre v 10-ih metih.
Na podoben način lahko obravnavamo verjetnost v našem primeru. Verjetnost, da pacient umre zaradi infarkta je \(p=0.04\), \(N = 10\), \(x\) pa je odvisen od naloge, ki jo rešujemo.
V programu Jamovi najprej dodamo nov modul v program z ukazom +Modules, kjer izberemo jamovi library (enako kot pri vaji pog. 1.4):
 V knjižnici modulov poiščemo modul distrACTION in ga namestimo v program:
V knjižnici modulov poiščemo modul distrACTION in ga namestimo v program:

Po namestitvi se nam nov modul pokaže v orodni vrstici programa Jamovi:

Kakšna je verjetnost, da noben od pacientov ne bo umrl?
Če želimo izračunati točno določen dogodek, v našem primeru točno določeno število pacientov, ki umrejo, uporabimo funkcijo \(PDF\). Imamo binomsko porazdelitev podatkov, saj imamo dva možna izida (pacient umre, pacient ne umre).
V našem primeru moramo izračunati \(p = PDF (X = 0)\) pri binomsko porazdeljeni spremenljivki \(x\). To se z uporabo modula distrACTION v Jamovi izvede z distrACTION -> Binomial Distribution.
V levem oknu izberemo ustrezne parametre binomske porazdelitve, torej velikost 10 in verjetnost, da pacient umre zaradi infarkta 0.04. Izračunamo verjetnost, da noben pacient ne umre z ukazom Compute probability z izbiro \(P(X = x1)\), pri čemer je x1 enak 0.
 V desnem oknu dobimo rezultate izračuna in sicer verjetnost 0.665 in izris, katero verjetnost smo izračunali na podlagi binomske porazdelitve z našimi parametri.
V desnem oknu dobimo rezultate izračuna in sicer verjetnost 0.665 in izris, katero verjetnost smo izračunali na podlagi binomske porazdelitve z našimi parametri.
Obstaja 66,5 % verjetnost, da noben od pacientov ne bo umrl (p = 0.665).
Kakšna je verjetnost, da bo 1 pacient umrl?
Po enakem postopku izračunamo verjetnost, da bo 1 pacient umrl. Izračunamo \(p = PDF (X = 1)\) pri binomsko porazdeljeni spremenljivki \(x\) z distrACTION -> Binomial Distribution.
V levem oknu izberemo ustrezne parametre binomske porazdelitve, torej velikost 10 in verjetnost, da pacient umre zaradi infarkta 0.04. Izračunamo verjetnost, da umre en pacient z ukazom Compute probability, izbiro \(P(X = x1)\), pri čemer je x1 enak 1.
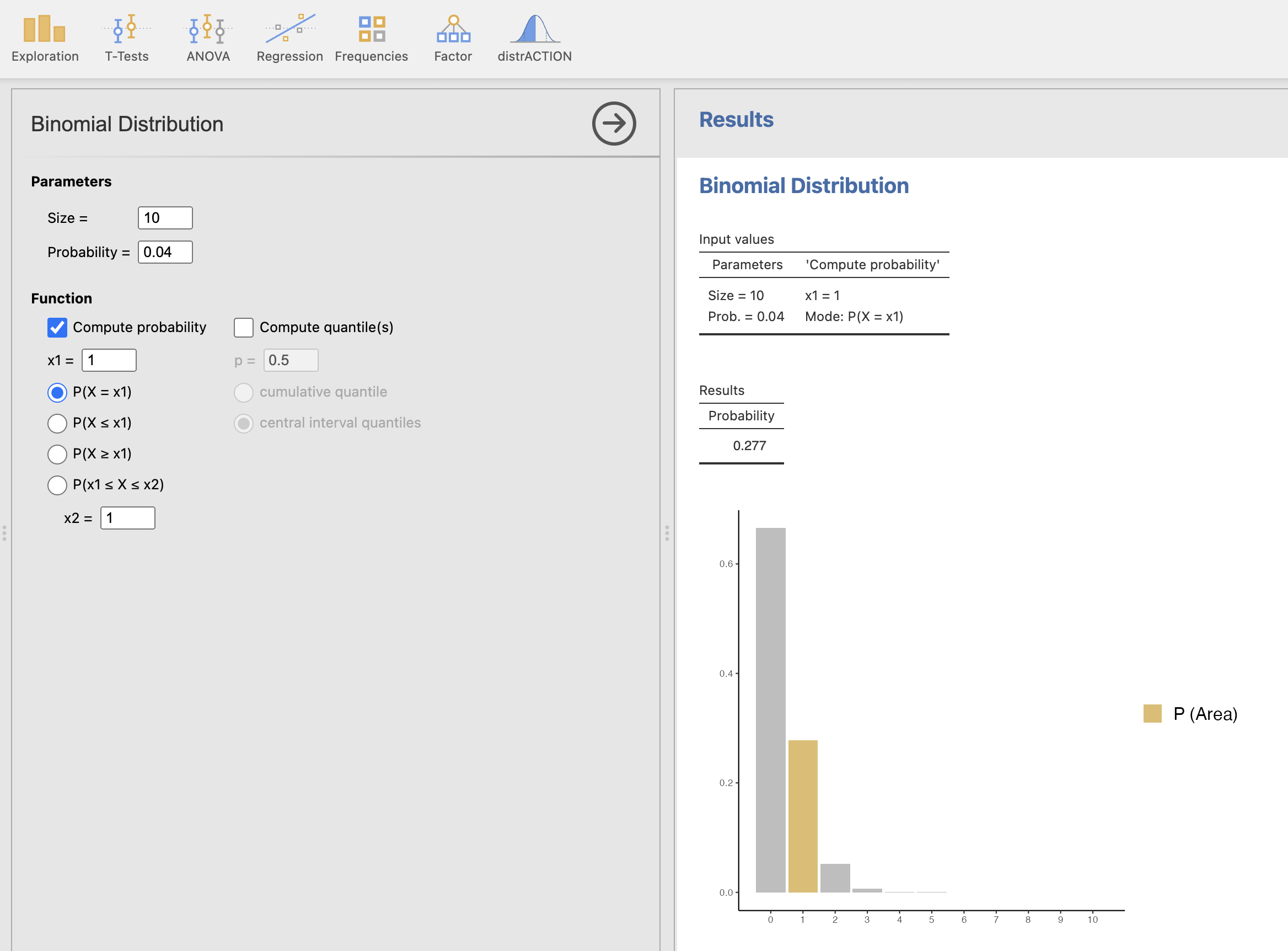 V desnem oknu dobimo rezultate izračuna in sicer verjetnost 0.277 in izris, katero verjetnost smo izračunali na podlagi binomske porazdelitve z našimi parametri.
V desnem oknu dobimo rezultate izračuna in sicer verjetnost 0.277 in izris, katero verjetnost smo izračunali na podlagi binomske porazdelitve z našimi parametri.
Obstaja 27,7 % verjetnost, da bo umrl en pacient (p = 0.277).
Kakšna je verjetnost, da bo polovica pacientov umrla?
Zanima nas, kakšna je verjetnost, da umre pet od desetih pacientov. Uporabimo enak postopek kot prej in izračunamo verjetnost, da bo umrlo pet pacientov. Izračunamo \(p = PDF (X = 5)\) pri binomsko porazdeljeni spremenljivki \(x\) z distrACTION -> Binomial Distribution.
V levem oknu izberemo ustrezne parametre binomske porazdelitve, torej velikost 10 in verjetnost, da pacient umre zaradi infarkta 0.04. Izračunamo verjetnost, da umre pet pacientov z ukazom Compute probability, izbiro \(P(X = x1)\), pri čemer je x1 enak 5.
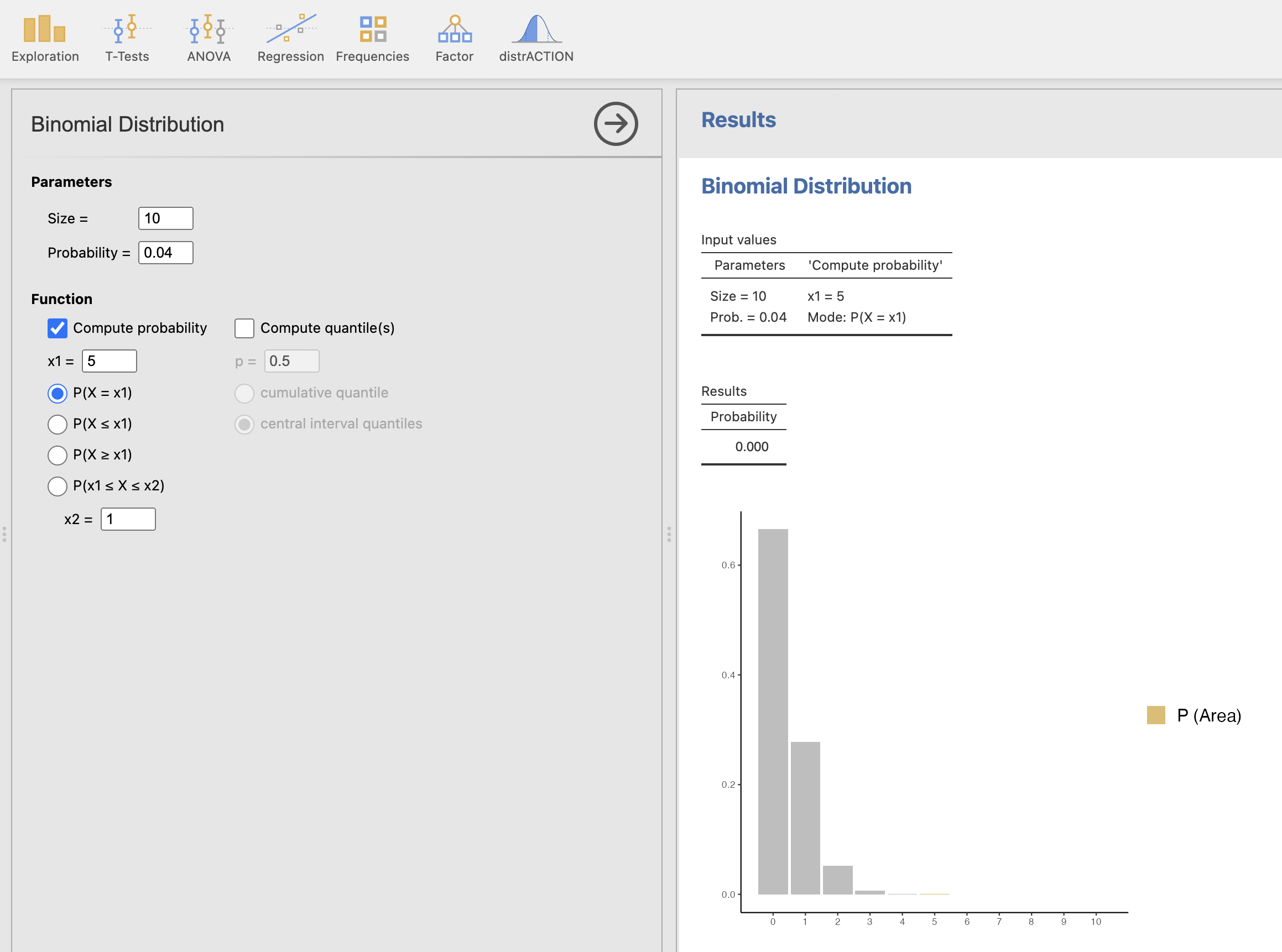 V desnem oknu dobimo rezultate izračuna in sicer zelo majhno verjetnost, ki je manjša od 0.000 in izris, katero verjetnost smo izračunali na podlagi binomske porazdelitve z našimi parametri.
V desnem oknu dobimo rezultate izračuna in sicer zelo majhno verjetnost, ki je manjša od 0.000 in izris, katero verjetnost smo izračunali na podlagi binomske porazdelitve z našimi parametri.
Obstaja zelo majhna verjetnost (manj kot 0 %), da bo polovica pacientov umrla (p < 0.000).
Če poznamo porazdelitev meritev in želimo izračunati verjetnost točno konkretnega dogodka, za izračun verjetnosti uporabimo funkcijo \(PDF\).
V našem primeru, ko imamo dve možnosti izida – pacient lahko umre ali ne umre, uporabimo binomsko porazdelitev za izračune konkretnih verjetnosti.