5 Preverjanje hipotez

5.1 Statistične primerjave dveh neodvisnih vzorcev

Navodila vaje

V datoteki AF_EKG.xlsx so zbrani podatki o pacientih z atrijsko fibrilacijo (AF) po operaciji na srcu (Kališnik et al. 2015). Zbranih je veliko podatkov: nekaj je o samih pacientih in koliko časa so ostali na intenzivni negi (ICU), ostali parametri pa so parametri EKG, ki smo jih merili pred operacijo.

Zanima nas, kateri parametri so statistično značilno različni pri pacientih z in brez AF.

Izvedite ustrezno statistično analizo:
1. Izračunajte opisne statistike vseh parametrov in jih ustrezno zapišite v tabelo.
2. Preverite normalno porazdelitev meritev in se odločite, katere statistične teste bomo uporabili pri analizi.
3. Podatke o deležih (kategorijske spremenljivke) preverite s testom za deleže.
4. Komentirajte rezultate in podajte zaključke analize.

Postopek reševanja

Z Jamovi preberemo podatke iz naloge za statistično analizo z ukazom Open in izbiro ustrezne datoteke AF_EKG.xlsx.

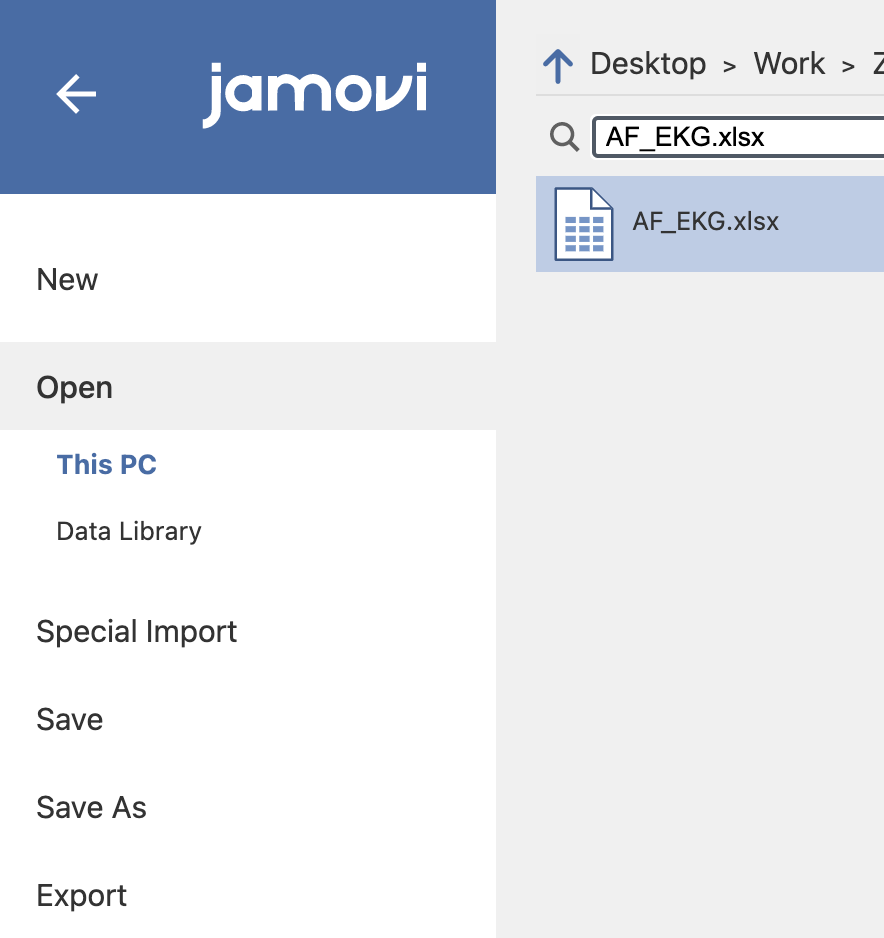
Sedaj moramo datoteko ustrezno popraviti, ker se podatki niso povsem ustrezno uvozili iz Excelove tabele. Pobrisali bomo prazne vrstice v zavihku Data od 89. vrstice do 122. vrstice. To storimo tako, da označimo vrstice, ki jih želimo izbrisati, pritisnemo desni miškin klik in izberemo Delete Rows.

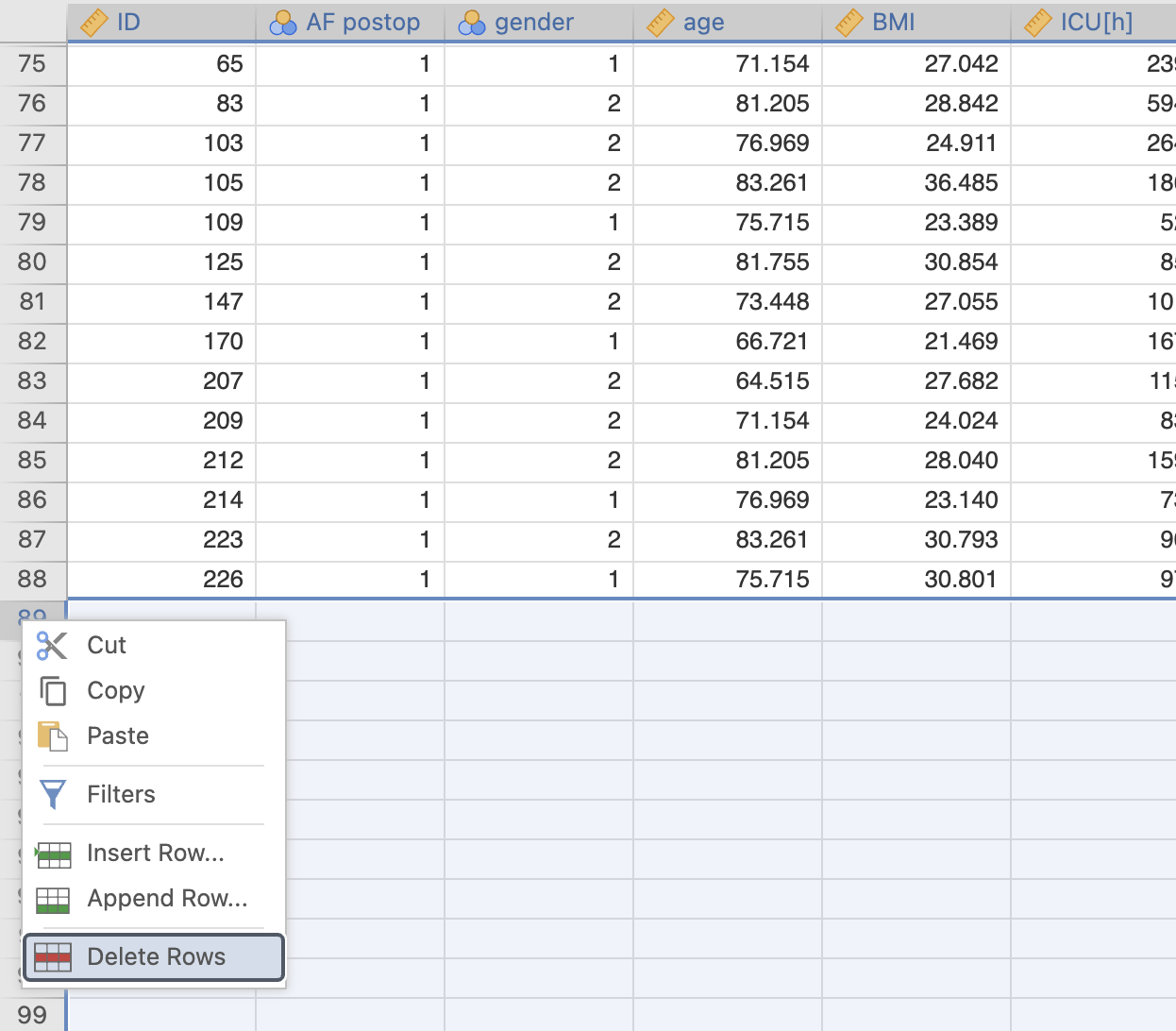
V zavihku Variables pobrišemo stolpce od AG naprej do konca. To storimo tako, da označimo spremenljivke/stolpce, ki jih želimo izbrisati in izberemo Delete.

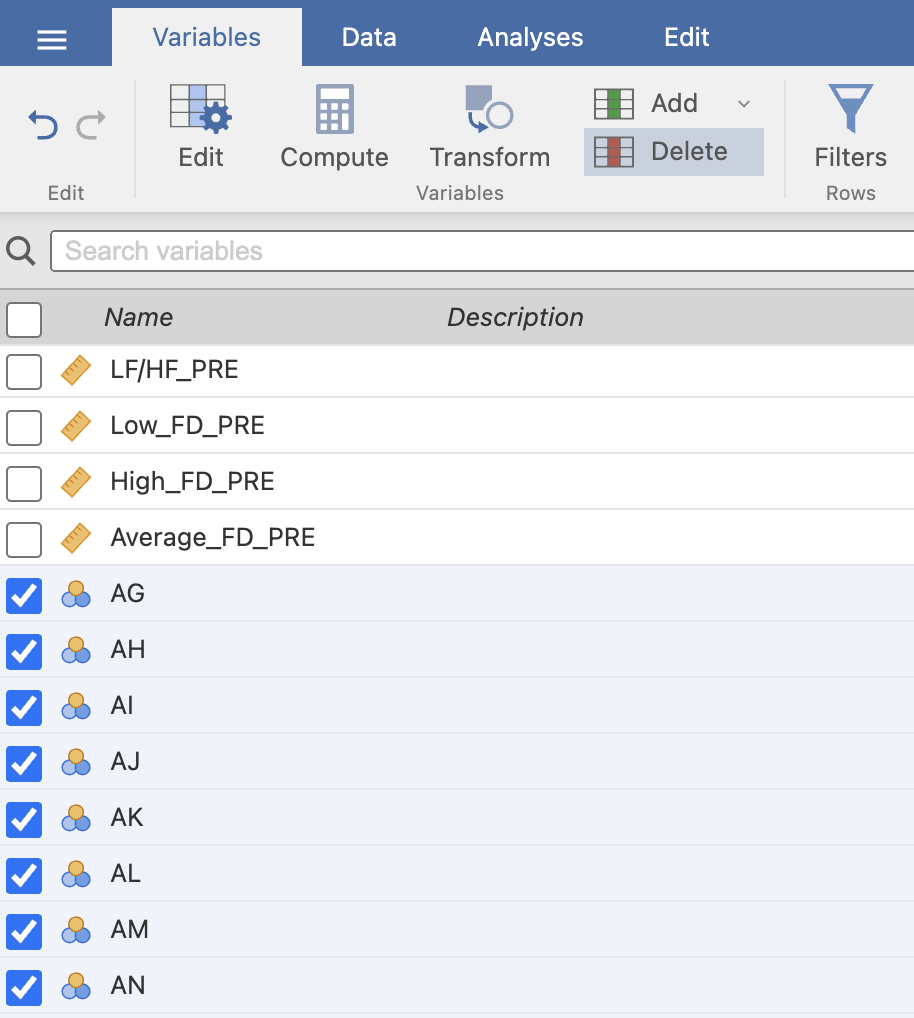
V zavihku Variables preverimo še ali so spremenljivke pravilno definirane. Opazimo, da je spremenljivka Pd definirana kot kategorijska spremenljivka, zato jo z ukazom Edit uredimo tako, da kot tip spremenljivke izberemo Continuous, saj je to skalarna spremenljivka.

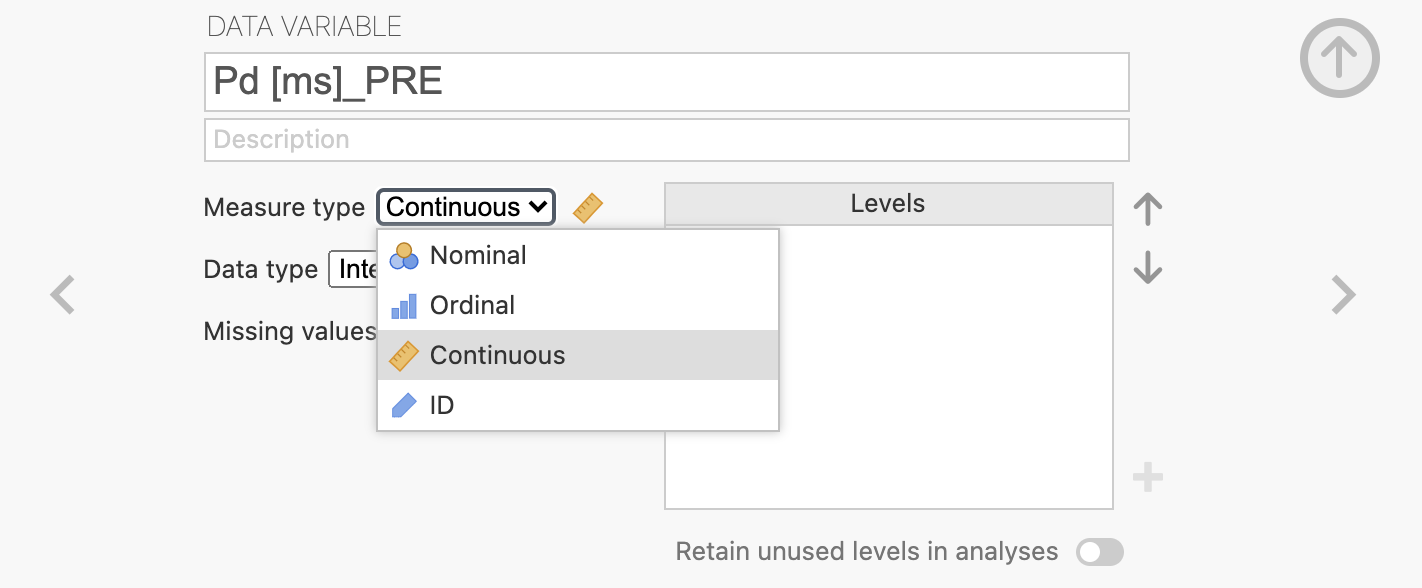
Tako smo podatke uredili in so ustrezno pripravljeni za analizo.

Zanima nas ali obstajajo statistično značilne razlike med pacienti, pri katerih ni prišlo do pojava atrijske fibrilacije in pacienti, pri katerih je prišlo do pojava atrijske fibrilacije (AF). Zanimajo nas torej razlike med skupino AF = 0 in AF = 1 v naslednjih parametrih: spol, starost, BMI, Pd, PQ, QTc Framingham, alfa 1 in alfa 2.

Zato predpostavimo naslednje hipoteze, ki jih bomo preverjali:

H₀:

Deleži med spoloma med skupinama z in brez AF se statistično značilno ne razlikujejo.
Povprečje starosti med skupinama z in brez AF se statistično značilno ne razlikujejo.
Povprečje BMI med skupinama z in brez AF se statistično značilno ne razlikujejo.
Povprečje Pd med skupinama z in brez AF se statistično značilno ne razlikujejo.
Povprečje PQ med skupinama z in brez AF se statistično značilno ne razlikujejo.
Povprečje QTc Framingham med skupinama z in brez AF se statistično značilno ne razlikujejo.
Povprečje alfa1 med skupinama z in brez AF se statistično značilno ne razlikujejo.
Povprečje alfa2 med skupinama z in brez AF se statistično značilno ne razlikujejo.

H₁:

Deleži med spoloma med skupinama z in brez AF se statistično značilno razlikujejo.
Povprečje starosti med skupinama z in brez AF se statistično značilno razlikujejo.
Povprečje BMI med skupinama z in brez AF se statistično značilno razlikujejo.
Povprečje Pd med skupinama z in brez AF se statistično značilno razlikujejo.
Povprečje PQ med skupinama z in brez AF se statistično značilno razlikujejo.
Povprečje QTc Framingham med skupinama z in brez AF se statistično značilno razlikujejo.
Povprečje alfa1 med skupinama z in brez AF se statistično značilno razlikujejo.
Povprečje alfa2 med skupinama z in brez AF se statistično značilno razlikujejo.

Najprej bomo izvedli osnovno opisno statistiko parametrov.

Spol je kategorijska spremenljivka. Za kategorijske spremenljivke izračunamo osnovno opisno statistiko z ukazom Analyses -> Exploration -> Descriptives.

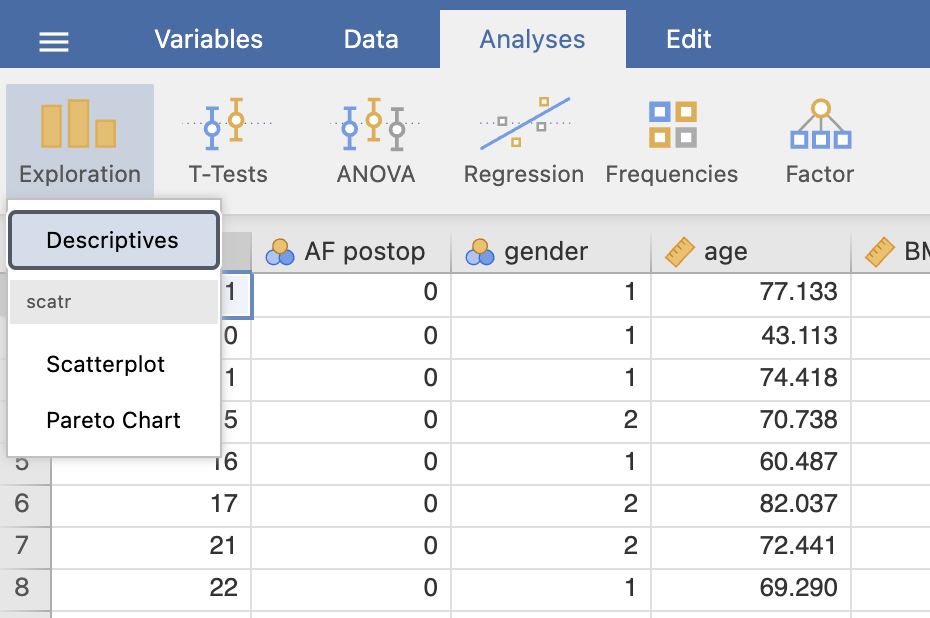
V oknu Descriptives pod Variables izberemo kategorijsko spremenljivko gender, pod Split by pa izberemo spremenljivko AF postop in označimo možnost Frequency tables za izpis frekvenčne tabele.

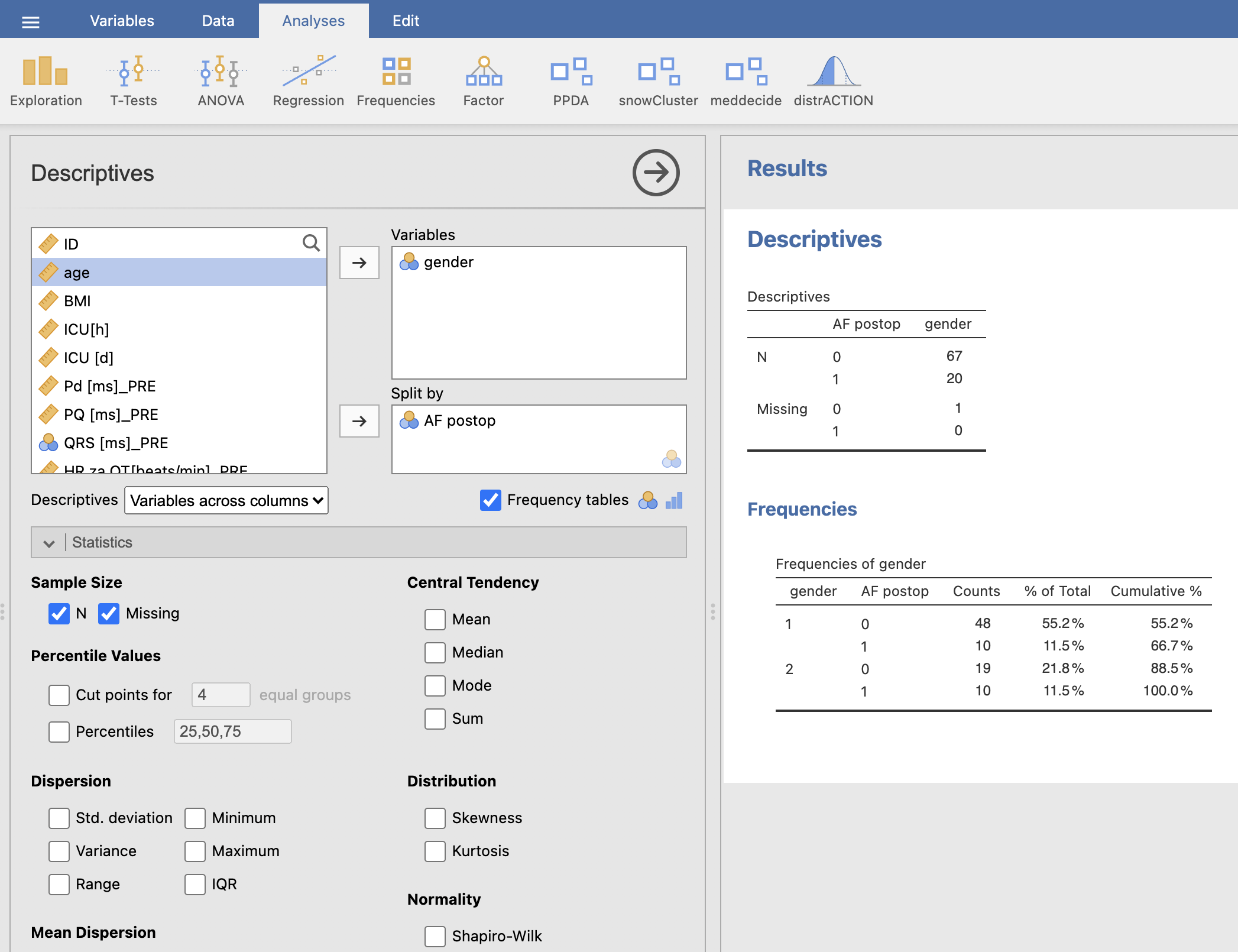
V desnem oknu Results se izpiše frekvenčna tabela iz katere razberemo podatke:

V skupini AF = 0 je 48 moških (gender = 1) in 19 žensk (gender = 2), skupaj 67 (N = 67). V skupini AF = 1 je 10 moških in 10 žensk, skupaj 20 (N = 20).

Izvedemo še opisno statistiko za skalarne spremenljivke:

Analyses -> Exploration -> Descriptives, pod Variables izberemo spremenljivke age, BMI, Pd, PQ, QTcFramingham, alfa1, alfa2, pod Split by pa spremenljivko delitve naših podatkov AF postop. V razdelku Statistics pri Normality izberemo Shapiro-Wilk, saj nas zanimajo še testi normalnosti.

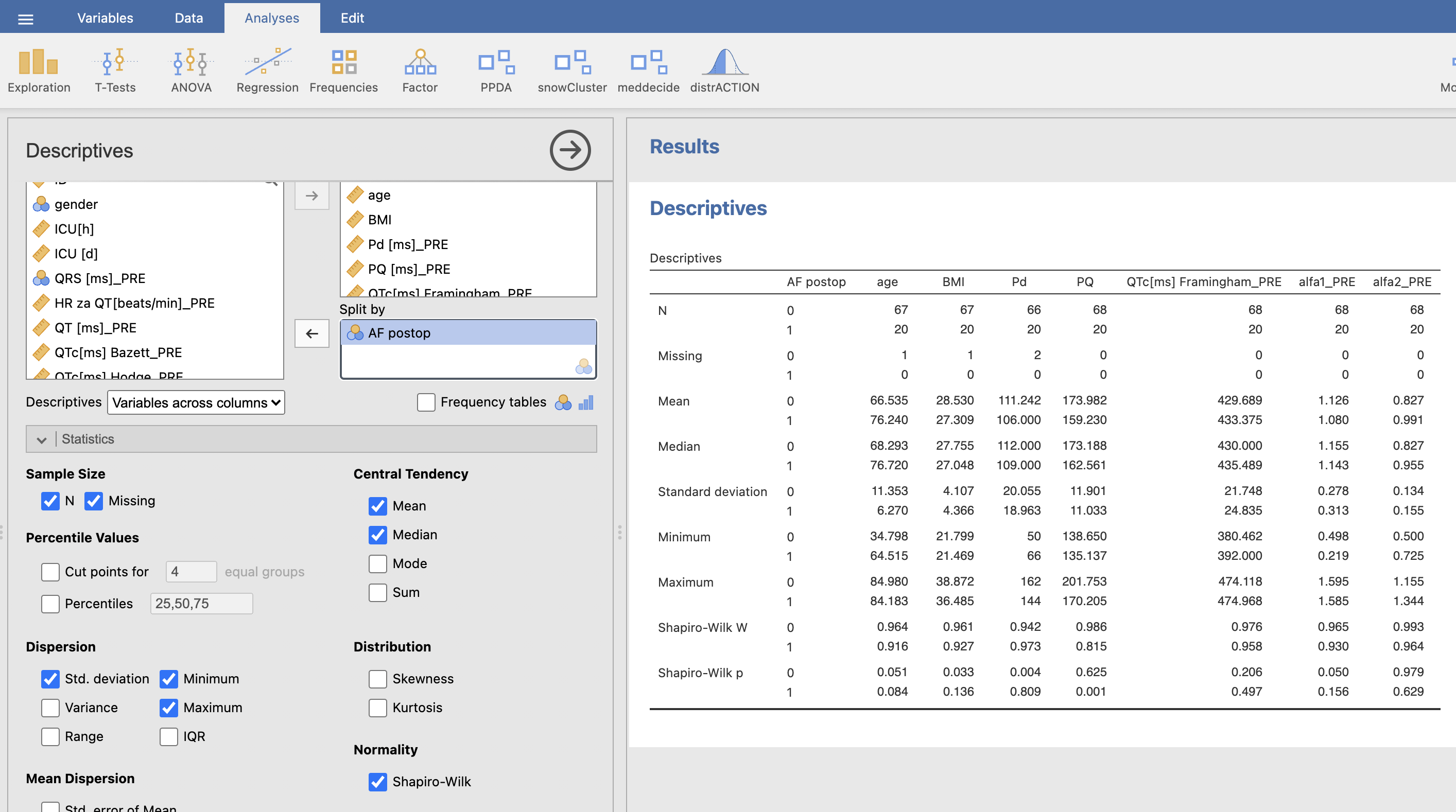
V desnem oknu Results se nam izpiše naslednja tabela iz katere razberemo osnovne parametre spremenljivk in odčitamo kakšne vrste podatkov imamo glede na normalnost.

Ugotovimo, da so starost, QTc Framingham, alfa 1 in alfa 2 normalno porazdeljeni, medtem ko BMI, Pd in PQ niso normalno porazdeljeni.

Pripravimo skupno tabelo iz naših analiz, v katero vpisujemo rezultate. Kategorijske spremenljivke zapisujemo kot deleže, skalarne spremenljivke pa kot povprečje ± standardni odklon. Tabela prikazuje podatke po opravljeni opisni statistiki vseh spremenljivk.

	AF = 0 (N = 67)	AF = 1 (N = 20)
Spol (M/Ž)	48/19	10/10
Starost	66.5 ± 11.4	76.2 ± 6.3
BMI*	28.5 ± 4.1	27.3 ± 4.4
Pd*	111.2 ± 20.1	106.0 ± 19.0
PQ*	174.0 ± 11.9	159.2 ± 11.0
QTc Framingham	429.7 ± 21.7	433.4 ± 24.8
alfa1	1.13 ± 0.28	1.08 ± 0.31
alfa2	0.83 ± 0.13	0.99 ± 0.15

Z * označimo spremenljivke, ki niso normalno porazdeljene.

Na podlagi porazdelitev podatkov izberemo ustrezen statistični test za primerjavo.

V primeru skalarnih spremenljivk, ki so normalno porazdeljene, bomo med sabo primerjali povprečne vrednosti, zato bomo uporabili t-test. Za primerjavo skalarnih spremenljivk, ki niso normalno porazdeljene pa uporabimo Mann Whitney U test. V primeru kategorijskih spremenljivk med seboj primerjamo deleže s hi-kvadrat testom.

S hi-kvadrat testom bomo med seboj primerjali deleže z ukazom Analyses -> Frequencies in pod Contingency Tables izberemo Independent Samples χ2 test of assosiation.

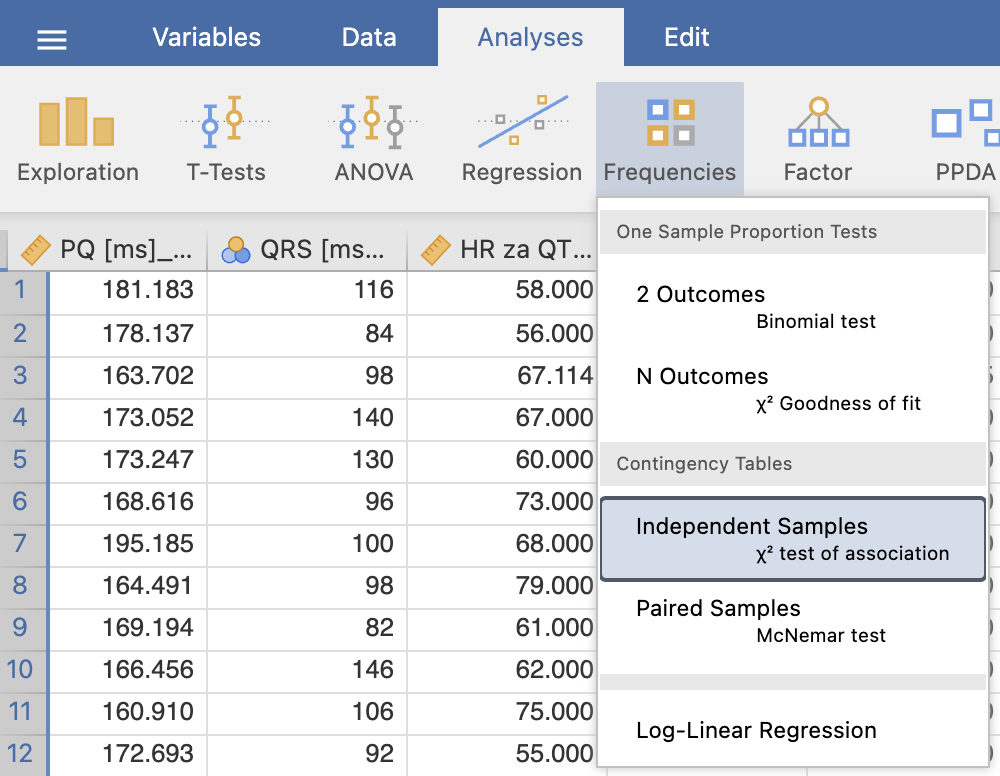
V levem oknu Contingency Tables izberemo, katera kategorijska spremenljivka bo izpisana v vrsticah (Rows = gender) in v stolpcih (Columns = AF postop) kontingenčne tabele. Pod razdelkom Statistics označimo Chi-square.

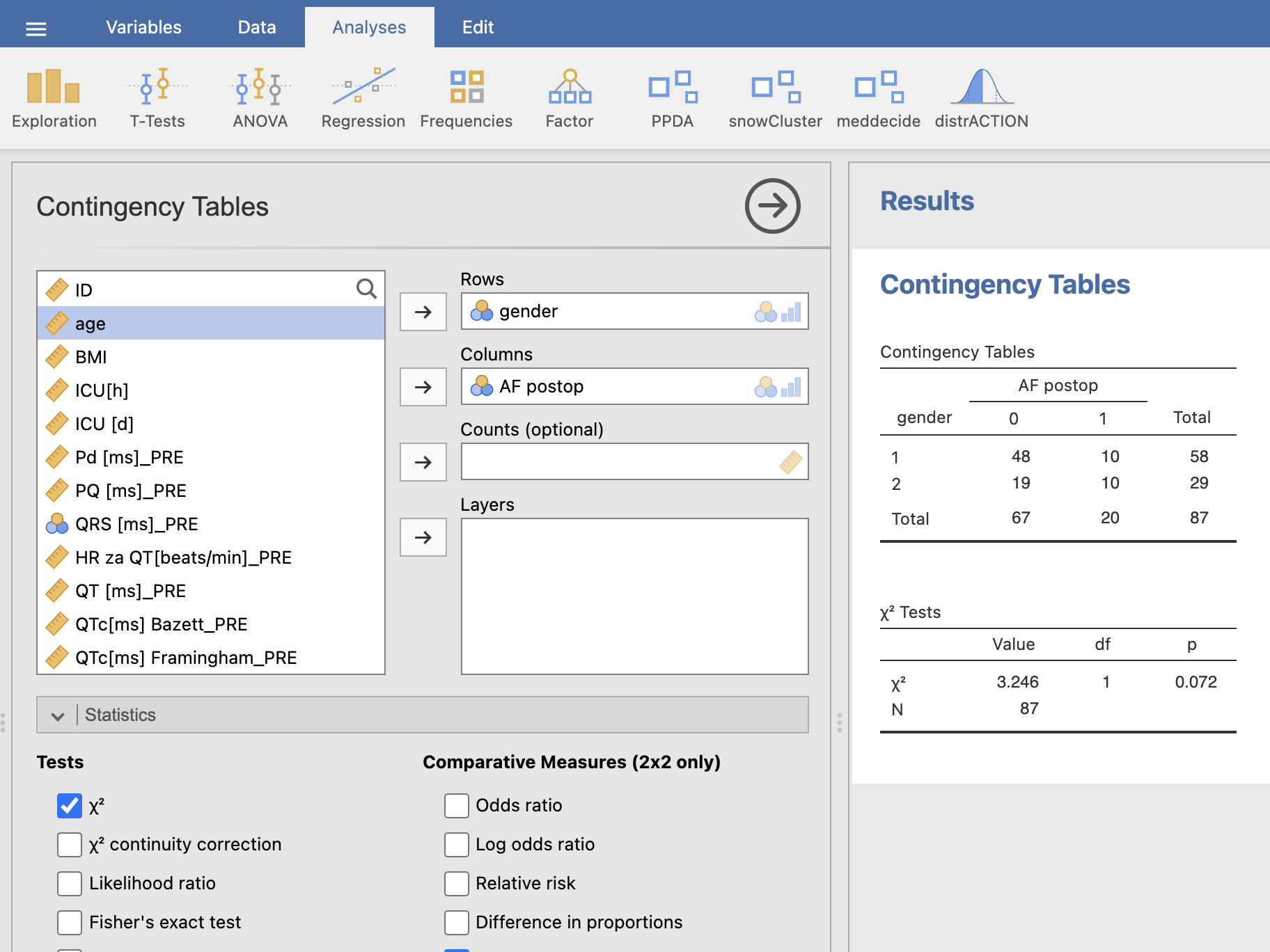
V oknu Results se nam izpiše kontingenčna tabela in tabela hi-kvadrat testa. P-vrednost je enaka 0.072.

Za primerjavo dveh neodvisnih vzorcev, ki sta normalno porazdeljena uporabimo t-test za neodvisne spremenljivke z ukazom Analyses -> T-Tests -> Independent Samples T-Test

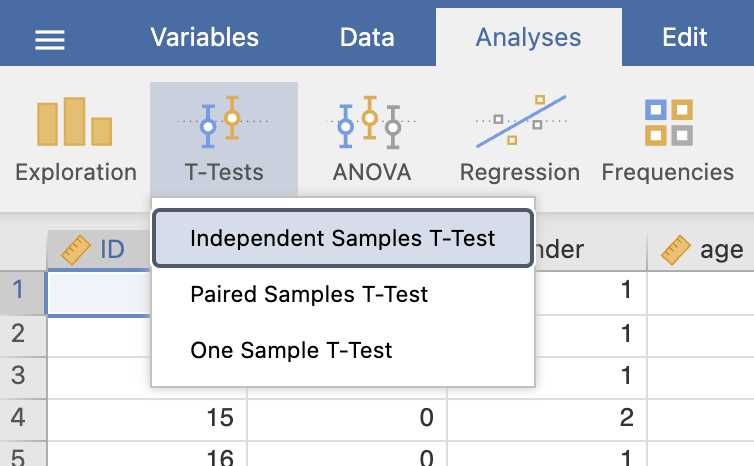
V oknu Independent Samples T-Test izberemo spremenljivke, ki so normalno porazdeljene in jih vstavimo v Dependent Variables. Pod Grouping Variable izberemo spremenljivko AF postop. Pod Tests moramo izbrati Student’s.

p-vrednosti vpišemo v tabelo iz tabele izpisane v desnem oknu Results:

	AF = 0 (N = 67)	AF = 1 (N = 20)	p- vrednost
Spol (M/Ž)	48/19	10/10	0.072
Starost	66.2 ± 11.3	76.2 ± 6.3	< 0.001
BMI*	28.5 ± 14.1	27.3 ± 4.4
Pd*	111.1 ± 20.2	106.0 ± 19.0
PQ*	174.0 ± 12.1	159.2 ± 11.0
QTc Framingham	428.5 ± 21.1	433.4 ± 24.8	0.521
alfa1	1.13 ± 0.28	1.08 ± 0.31	0.531
alfa2	0.83 ± 0.13	0.99 ± 0.16	< 0.001

* meritve niso normalno porazdeljene

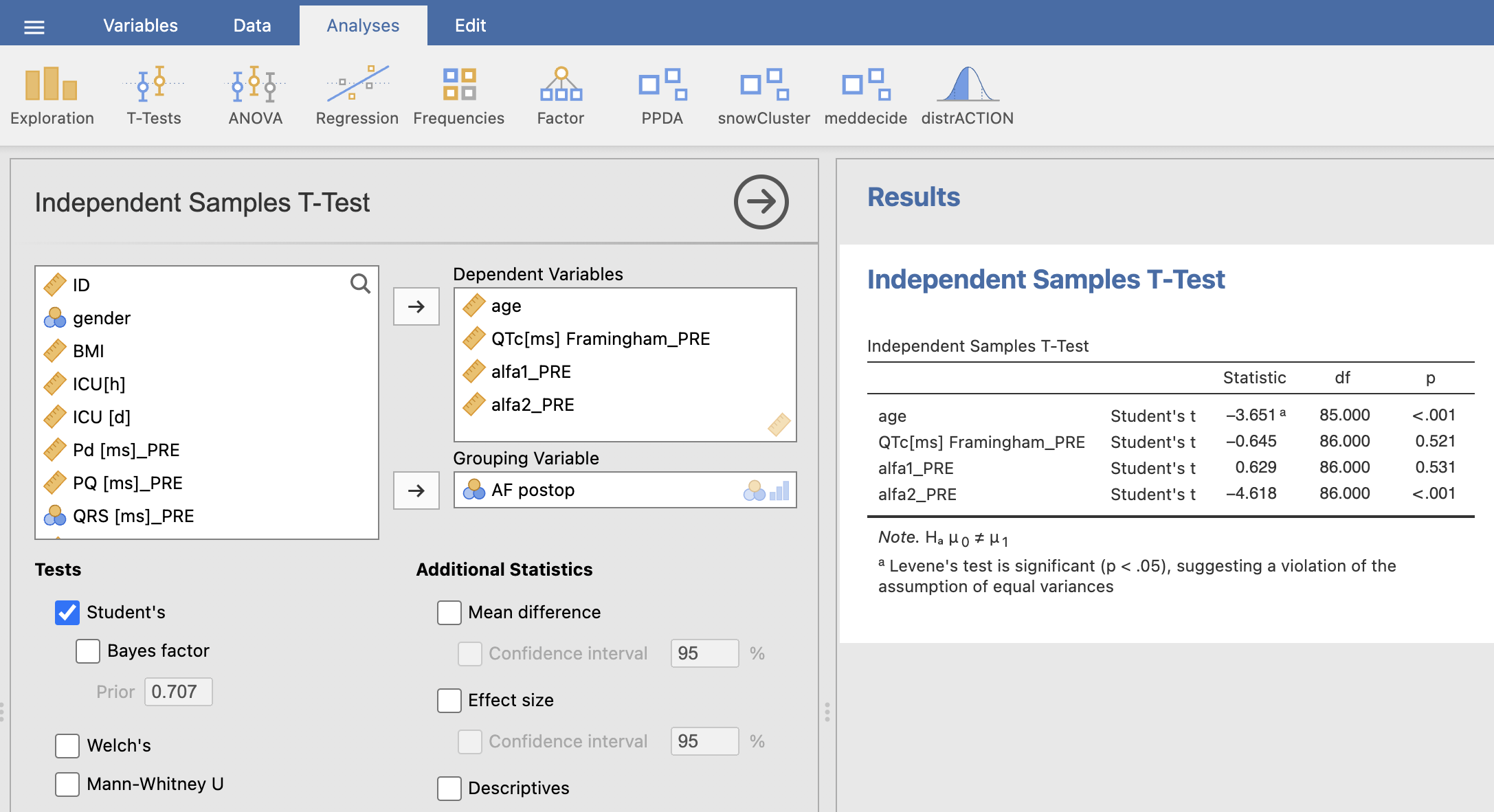
Za primerjavo dveh neodvisnih vzorcev, ki nista normalno porazdeljena uporabimo Mann Whitney U test z ukazom Analyses -> T-Tests -> Independent Samples T-Test.

V oknu Independent Samples T-Test izberemo spremenljivke, ki niso normalno porazdeljene in jih vstavimo v Dependent Variables. Pod Grouping Variable izberemo spremenljivko, ki predstavlja dve skupini: AF postop. Pod Tests moramo izbrati Mann-Whitney U.

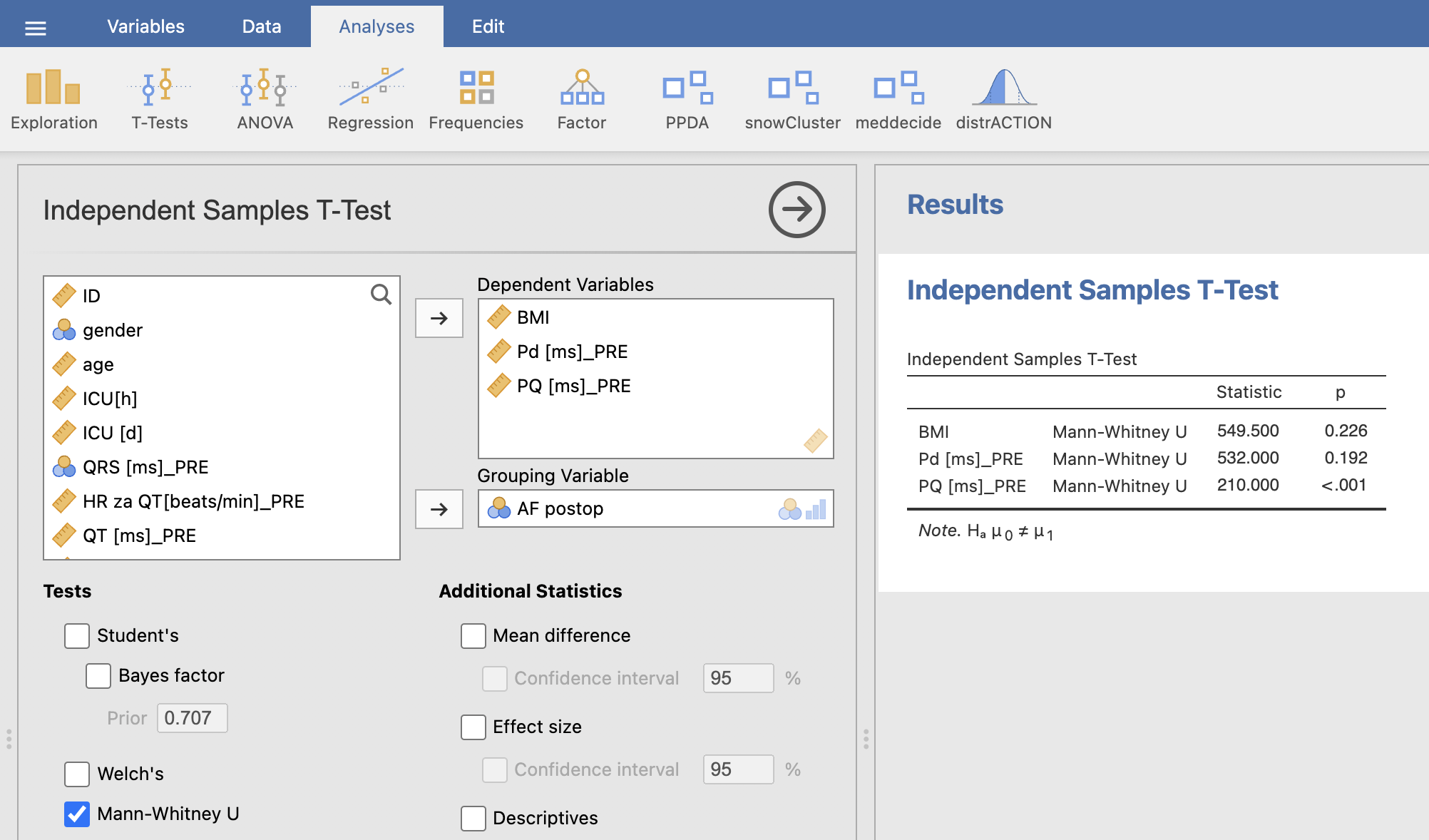
V oknu Results se izpiše tabela z rezultati neparametričnega Mann-Whitney U testa. p-vrednosti zapišemo v našo tabelo. Tako dobimo končno tabelo:

	AF = 0 (N = 67)	AF = 1 (N = 20)	p- vrednost
Spol (M/Ž)	48/19	10/10	0.072
Starost	66.2 ± 11.3	76.2 ± 6.3	< 0.001
BMI*	28.5 ± 14.1	27.3 ± 4.4	0.226
Pd*	111.1 ± 20.2	106.0 ± 19.0	0.192
PQ*	174.0 ± 12.1	159.2 ± 11.0	< 0.001
QTc Framingham	428.5 ± 21.1	433.4 ± 24.8	0.521
alfa1	1.13 ± 0.28	1.08 ± 0.31	0.531
alfa2	0.83 ± 0.13	0.99 ± 0.16	< 0.001

* meritve niso normalno porazdeljene

Končne ugotovitve

Statistična metodologija:

Razlike med skupinama pacientov brez in z atrijsko fibrilacijo smo preverjali z uporabo naslednjih statističnih testov: t-testa dveh neodvisnih vzorcev v primeru normalno porazdeljenih podatkov in z uporabo Mann Whitney U testa v primeru, ko podatki niso bili normalno porazdeljeni. Normalno porazdelitev smo testirali z uporabo Shapiro-Wilkovega testa. Kategorijske spremenljivke smo testirali z uporabo hi-kvadrat testa. Podatki v tabelah so podani v obliki povprečje ± standardni odklon. Meja za statistično značilnost je postavljana pri p < 0.05. Statistična analiza je bila narejena s programom Jamovi.

Rezultati:

Iz rezultatov statistične analize smo ugotovili, da obstajajo statistično značilne razlike med skupinama z in brez atrijske fibrilacije pri starosti (p < 0.001), PQ (p < 0.001) in alfa 2 (p < 0.001). Statistično značilnih razlik pa ne ugotovimo pri BMI (p = 0.226), Pd (p = 0.192), QTc Framingham (p = 0.521) in alfa 1 (p = 0.531). Statistično značilnih razlik med skupinama tudi ne moremo potrditi pri kategorijski spremenljivki spol (p = 0.072).

5.2 Statistične primerjave dveh odvisnih vzorcev

Navodila vaje

V datoteki AF_EKG_pre_post.xlsx so zbrani podatki o pacientih z atrijsko fibrilacijo po operaciji na srcu (Kališnik et al. 2015). Tokrat imamo podatke o EKG parametrih še izmerjene dvakrat po operaciji, vendar pred nastopom atrijske fibrilacije.

Zanima nas, ali obstajajo statistično značilne razlike med parametri pred in po operaciji.

Izvedi ustrezne statistične analize ločeno glede na AF = 0 in AF = 1. Podatke ustrezno predstavi. Ugotovi, ali so meritve normalno porazdeljene. Nato izvedi ustrezen test.
Rezultate predstavi v končni tabeli in jih komentiraj.

Postopek reševanja

Odpremo podatke iz naloge za statistično analizo z ukazom Open in izbiro ustrezne datoteke AF_EKG_pre_post.xlsx.

Nato izbrišemo ‘’prazne’’ podatke v Data in tudi v Variables. V Variables preverimo, če so tipi spremenljivk pravilno določeni. Nekatere spremenljivke moramo ustrezno popraviti v skalarje. To naredimo z ukazom Edit in izbiro Measure type = Continuous. Vse spremenljivke, z izjemo AF postop in gender, so skalarji.

Primerjali bomo izbrane spremenljivke (Pd, PQ, QTcFramingham, alfa1, alfa2) pred operacijo na srcu in po operaciji na srcu za paciente z atrijsko fibrilacijo (AF = 1) in za paciente brez atrijske fibrilacije (AF = 0).

V programu Jamovi bomo obravnavo teh dveh skupin izvedli ločeno z uporabo ustreznega filtra - izberemo možnost Filters.

V odprtem oknu ustrezno določimo, da bomo obravnavali le paciente, ki niso imeli atrijske fibrilacije (AF = 0). V zavihku Data se nam izpiše novi stolpec, ki označuje, katere podatke bomo uporabili za analizo.

Zanimajo nas povprečne vrednosti in standardni odkloni za vsako izmed spremenljivk. Hkrati bomo preverili ali so spremenljivke normalno porazdeljene. Na podlagi porazdelitev, se bomo odločili katere teste bomo uporabili za ugotavljanje statistično značilnih razlik.

To izvedemo z ukazom: Analyses -> Exploration -> Descriptives, kjer v Variables dodamo željene spremenljivke, z izbiro Normality - Shapiro-Wilk v razdelku Statistics pa izberemo izračun testov normalnosti.

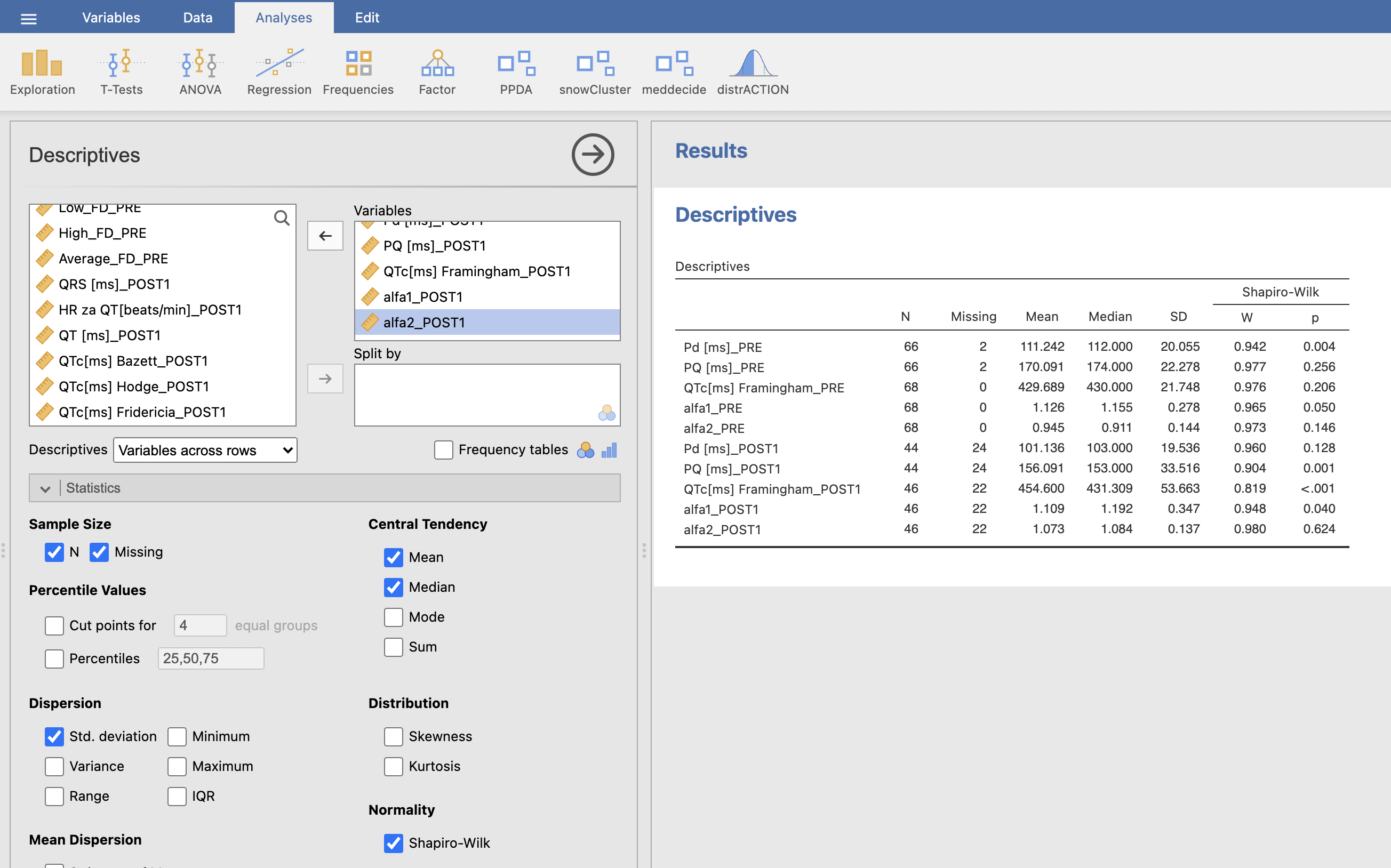
Iz dobljenih rezultatov izpišemo povprečje in standardni odklon za vsako spremenljivko posebej. V oknu Results je prikazana tabela rezultatov za paciente brez atrijske fibrilacije, ki smo jim merili določene parametre pred in po operaciji.

Ustvarimo si tabelo, kjer pregledno izpišemo podatke. Prva tabela prikazuje rezultate za paciente brez atrijske fibrilacije (AF = 0), druga tabela pa bo prikazovala rezultate za paciente z atrijsko fibrilacijo (AF = 1). Stolpec PRE prikazuje povprečne vrednosti in standardne odklone za določene spremenljivke pred operacijo, stolpec POST1 pa po operaciji.

	AF = 0
	PRE (povprečje ± SD)	POST1 (povprečje ± SD)
Pd	111.2 ± 20.1	101.1 ± 19.5
PQ	170.1 ± 22.3	156.1 ± 33.5
QTcFramingham	429.7 ± 21.7	454.6 ± 53.7
alfa1	1.13 ± 0.28	1.11 ± 0.35
alfa2	0.94 ± 0.14	1.07 ± 0.14

Postavimo si ničelne in alternativne hipoteze za AF = 0:

H₀:

Razlika med povprečjema Pd pred operacijo in Pd po operaciji pri pacientih brez atrijske fibrilacije je enaka 0.
Razlika med povprečjema PQ pred operacijo in PQ po operaciji pri pacientih brez atrijske fibrilacije je enaka 0.
Razlika med povprečjema QTcFramingham pred operacijo in QTcFramingham po operaciji pri pacientih brez atrijske fibrilacije je enaka 0.
Razlika med povprečjema alfa1 pred operacijo in alfa1 po operaciji pri pacientih brez atrijske fibrilacije je enaka 0.
Razlika med povprečjema alfa2 pred operacijo in alfa2 po operaciji pri pacientih brez atrijske fibrilacije je enaka 0.

H₁:

Razlika med povprečjema Pd pred operacijo in Pd po operaciji pri pacientih brez atrijske fibrilacije ni enaka 0.
Razlika med povprečjema PQ pred operacijo in PQ po operaciji pri pacientih brez atrijske fibrilacije ni enaka 0.
Razlika med povprečjema QTcFramingham pred operacijo in QTcFramingham po operaciji pri pacientih brez atrijske fibrilacije ni enaka 0.
Razlika med povprečjema alfa1 pred operacijo in alfa1 po operaciji pri pacientih brez atrijske fibrilacije ni enaka 0.
Razlika med povprečjema alfa2 pred operacijo in alfa2 po operaciji pri pacientih brez atrijske fibrilacije ni enaka 0.

S pomočjo Shapiro-Wilk testa za porazdelitev podatkov ugotovimo, da so spremenljivke PQ_PRE, QTcFramingham_PRE, alfa1_PRE, alfa2_PRED, Pd_POST1 in alfa2_POST1 za AF = 0 normalno porazdeljene, ostale spremenljivke pri AF = 0 pa niso normalno porazdeljene. Spremenljivke, ki niso normalno porazdeljene bomo v tabeli označili z *.

Pri ugotavljanju statistično značilnih razlik med alfa2 pred in po operaciji za skupino pacientov brez atrijske fibrilacije (AF = 0) bomo, zaradi normalne porazdelitve podatkov, uporabili parni t-test (Analyses -> T-Tests -> Paired Samples T-test).

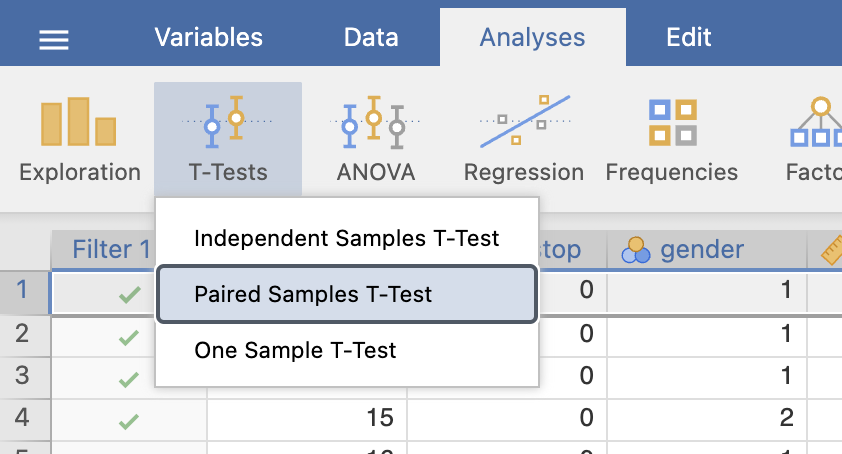
V oknu Paired Samples T-test pod Paired Variables določimo par spremenljivk: alfa2_PRE in alfa2_POST1. Pod možnostjo Tests moramo označiti možnost Student’s.

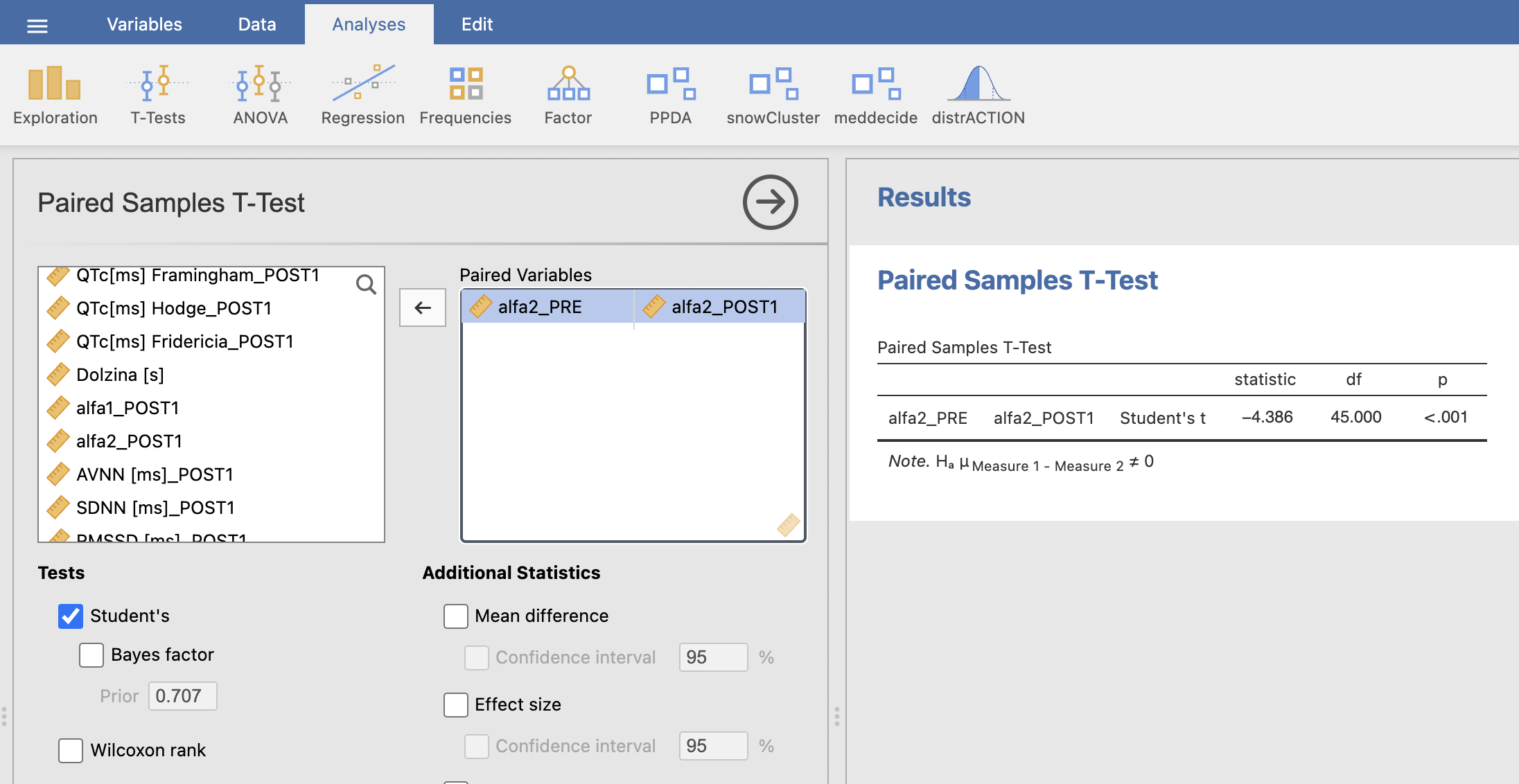
V Results se nam izpiše tabela parnega t-testa. Vrednost je p < 0.001. Ker je p-vrednost manjša od 0.05, lahko ničelno hipotezo ovržemo in sprejmemo alternativno hipotezo, ki pravi da obstajajo statistično značilne razlike med povprečno vrednostjo alfa2 pred operacijo in po operaciji pri pacientih brez atrijske fibrilacije.

Pri ugotavljanju statistično značilnih razlik drugih spremenljivk pred in po operaciji za skupino pacientov brez atrijske fibrilacije (AF = 0) bomo zaradi podatkov, ki niso normalno porazdeljeni, uporabili Wilcoxonov test predznaka (Analyses -> T-Tests -> Paired Samples T-Test).

Zdaj pod Paired Variables določimo pare spremenljivk, kot je prikazano na sliki. Pod možnostjo Tests moramo označiti možnost Wilcoxon rank.

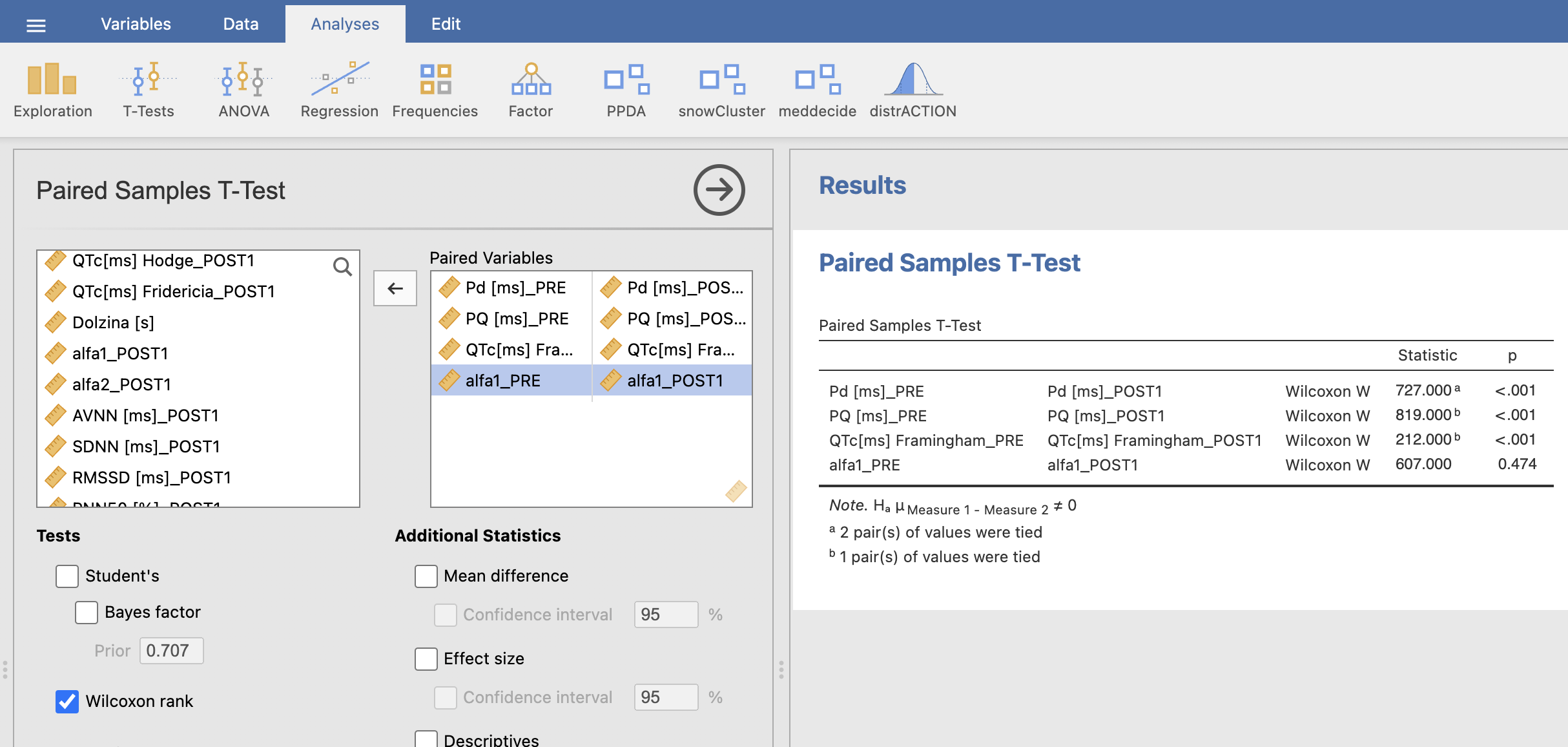
Iz okna Results razberemo p-vrednosti za vse spremenljivke pri AF = 0 in dopolnimo našo tabelo še s p-vrednostmi.

	AF = 0
	PRE (povprečje ± SD)	POST1 (povprečje ± SD)	p-vrednost
Pd*	111.2 ± 20.1	101.1 ± 19.5	<0.001
PQ*	170.1 ± 22.3	156.1 ± 33.5	<0.001
Q T cFramingham*	429.7 ± 21.7	454.6 ± 53.7	<0.001
alfa1*	1.13 ± 0.28	1.11 ± 0.35	0.474
alfa2	0.94 ± 0.14	1.07 ± 0.14	<0.001

Tako lahko ugotovimo, da statistično značilnih razlik v povprečni vrednosti alfa1 pred operacijo in po operaciji za paciente brez atrijske fibrilacije ni (p = 0.474). Pri ostalih spremenljivkah pa obstajajo statistično značilne razlike med povprečji pred in po operaciji pri pacientih brez atrijske fibrilacije.

Zdaj bomo naredili še analizo za paciente, ki so imeli atrijsko fibrilacijo (AF = 1). Z izbiro možnosti Filters in ustrezno izbiro filtra označimo, da obravnavamo le paciente, ki so imeli atrijsko fibrilacijo. V zavihku Data se v stolpcu Filter označijo podatki, ki jih bomo uporabili.

Zanimajo nas povprečne vrednosti in standardni odkloni za vsako izmed spremenljivk pri pacientih, ki so imeli atrijsko fibrilacijo. Preverili bomo tudi ali so spremenljivke normalno porazdeljene in se odločili katere teste bomo uporabili za ugotavljanje statistično značilnih razlik. Izvedimo ukaz: Analyses -> Exploration -> Descriptives, kjer v Variables dodamo spremenljivke, z izbiro Normality - Shapiro-Wilk v razdelku Statistics pa izberemo izračun testov normalnosti.

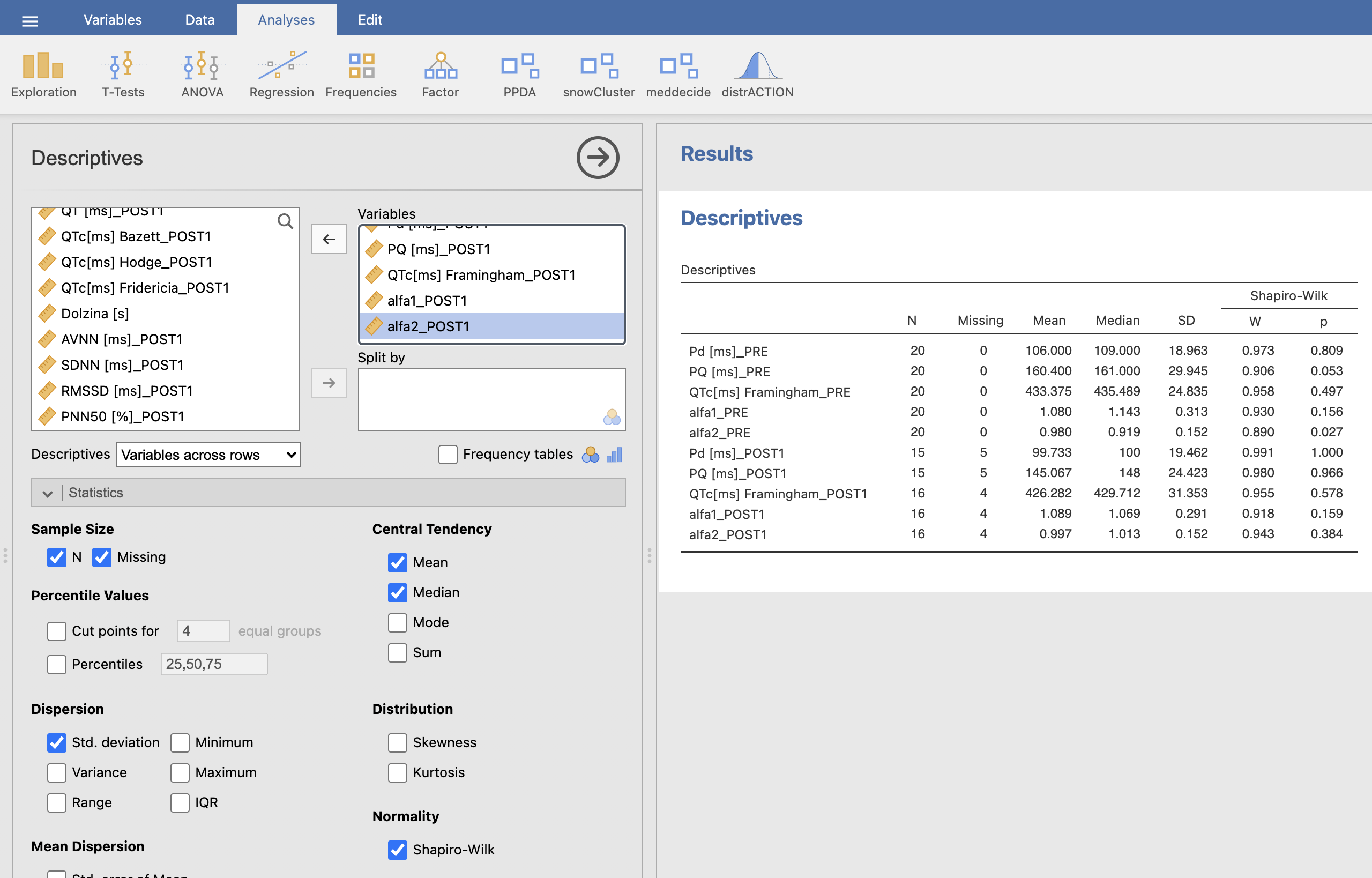
Iz dobljenih rezultatov izpišemo povprečje in standardni odklon za vsako spremenljivko posebej. V oknu Results je prikazana tabela rezultatov za paciente z atrijsko fibrilacijo, ki smo jim merili določene parametre pred in po operaciji.

Pri skupini pacientov z atrijsko fibrilacijo (AF = 1) smo s pomočjo Shapiro-Wilk testa za testiranje normalne porazdelitve podatkov ugotovili, da spremenljivka alfa2 ni normalno porazdeljena, medtem ko ostale spremenljivke so normalno porazdeljene.

Postavimo si ničelne in alternativne hipoteze za AF = 1:

H₀:

Razlika med povprečjema Pd pred operacijo in Pd po operaciji pri pacientih z atrijsko fibrilacijo je enaka 0.
Razlika med povprečjema PQ pred operacijo in PQ po operaciji pri pacientih z atrijsko fibrilacijo je enaka 0.
Razlika med povprečjema QTcFramingham pred operacijo in QTcFramingham po operaciji pri pacientih z atrijsko fibrilacijo je enaka 0.
Razlika med povprečjema alfa1 pred operacijo in alfa1 po operaciji pri pacientih z atrijsko fibrilacijo je enaka 0.
Razlika med povprečjema alfa2 pred operacijo in alfa2 po operaciji pri pacientih z atrijsko fibrilacijo je enaka 0.

H₁:

Razlika med povprečjema Pd pred operacijo in Pd po operaciji pri pacientih z atrijsko fibrilacijo ni enaka 0.
Razlika med povprečjema PQ pred operacijo in PQ po operaciji pri pacientih z atrijsko fibrilacijo ni enaka 0.
Razlika med povprečjema QTcFramingham pred operacijo in QTcFramingham po operaciji pri pacientih z atrijsko fibrilacijo ni enaka 0.
Razlika med povprečjema alfa1 pred operacijo in alfa1 po operaciji pri pacientih z atrijsko fibrilacijo ni enaka 0.
Razlika med povprečjema alfa2 pred operacijo in alfa2 po operaciji pri pacientih z atrijsko fibrilacijo ni enaka 0.

Za ugotavljanje statistično značilnih razlik pri spremenljivki alfa2 pred in po operaciji smo uporabili Wilcoxonov test predznaka (Analyses -> T-Tests -> Paired Samples T-Test -> Wilcoxon rank). Za ugotavljanje statistično značilnih razlik pri ostalih spremenljivkah pa smo uporabili parni t-test (Analyses -> T-Tests -> Paired Samples T-Test -> Student’s).

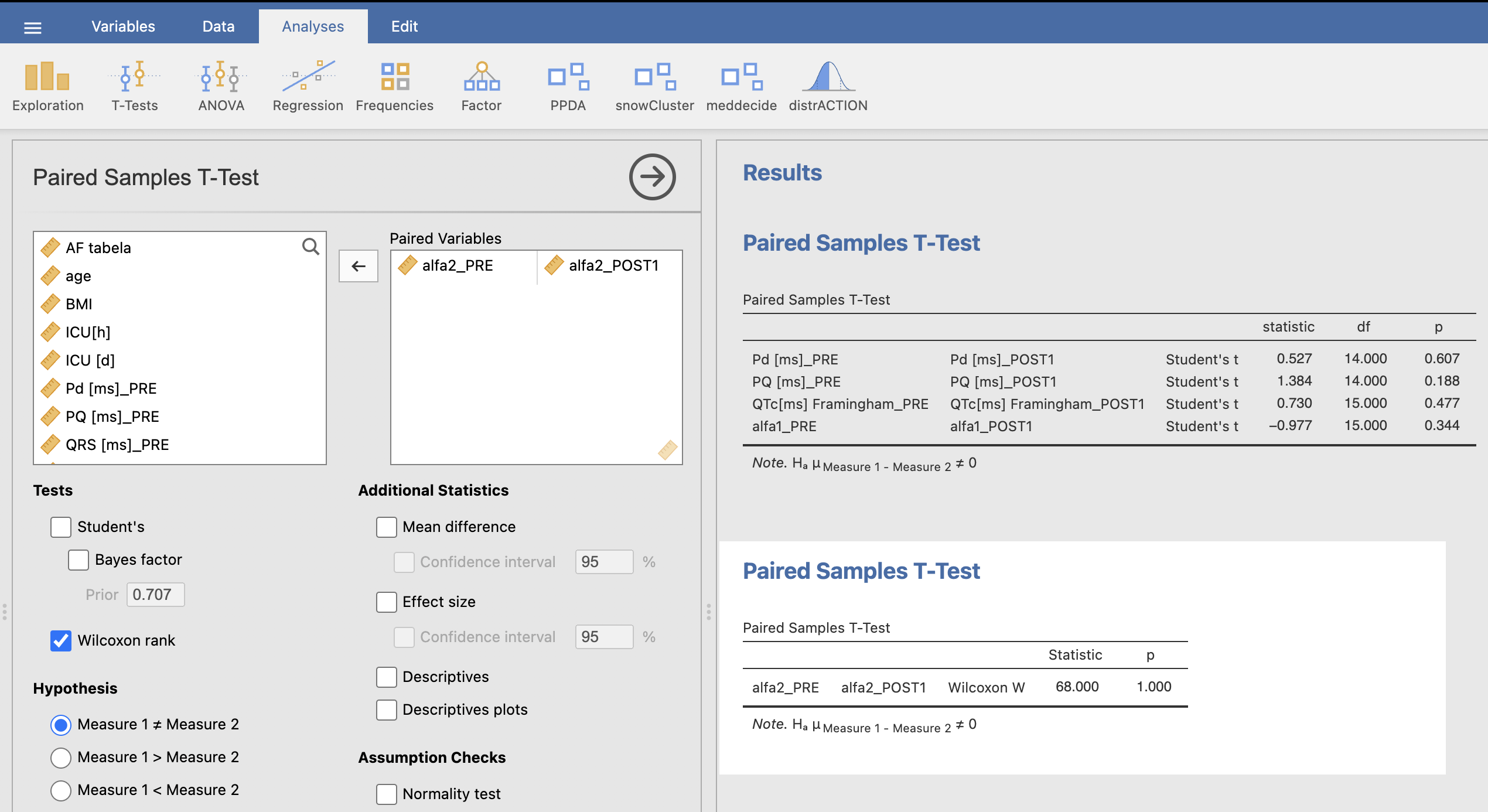
Spodnja tabela prikazuje rezultate za paciente z atrijsko fibrilacijo (AF = 1). Stolpec PRE prikazuje povprečne vrednosti in standardne odklone za določene spremenljivke pred operacijo, stolpec POST1 pa po operaciji. P-vrednosti prikazujejo rezultate ustreznih statističnih testov.

	AF = 1
	PRE (povprečje ± SD)	POST1 (povprečje ± SD)	p-vrednost
Pd	106.0 ± 19.0	99.7 ± 19.5	0.607
PQ	160.4 ± 30.0	145.1 ± 24.4	0.188
QTcFramingham	433.4 ± 24.8	426.3 ± 31.4	0.477
alfa1	1.08 ± 0.31	1.09 ± 0.29	0.344
alfa2	0.98 ± 0.15	1.00 ± 0.15	1.000

Ugotovimo, da statistično značilnih razlik med povprečji posameznih spremenljivk pred in po operaciji pri pacientih z atrijsko fibrilacijo ni, saj so vse p-vrednosti večje od 0.05, kar pomeni, da ničelnih hipotez ne moremo zavrniti.

Končne ugotovitve

Statistična metodologija:

S statistično analizo smo ugotavljali, ali obstajajo razlike med izbranimi EKG parametri pred in po operaciji. Statistično analizo smo izvajali ločeno pri pacientih z in brez atrijske fibrilacije. Statistično značilnost razlik smo preverjali z uporabo statističnih testov: parnega t-testa v primeru normalne porazdelitve podatkov in z uporabo Wilcoxon-ovega testa predznaka v primeru, ko podatki niso bili normalno porazdeljeni. Normalnost porazdelitve EKG parametrov smo testirali z uporabo Shapiro-Wilk testa.

Rezultate smo podali v dveh ločenih tabelah za skupino z atrijsko fibrilacijo in brez atrijske fibrilacije. Predstavljeni so bili v obliki povprečje ± standardni odklon s pripadajočo p-vrednostjo ustreznega statističnega testa. Meja za statistično značilnost je postavljena na p = 0.05.

Rezultati:

S statistično analizo smo ugotovili, da obstajajo statistično značilne razlike v vseh EKG parametrih v primeru skupine pacientov brez atrijske fibrilacije, razen v primeru parametra alfa1 (p = 0.474). V skupini pacientov z atrijsko fibrilacijo nismo ugotovili statistično značilnih razlik med analiziranimi EKG parametri (vse p-vrednosti > 0.05).

5.3 Testiranje podatkov v deležih

Navodila vaje

V datoteki koncna_anketa_o_izgorelosti.doc je predstavljena anketa, ki so jo izpolnjevali zaposleni v radiološki tehnologiji, s katero smo želeli ugotavljati stopnjo izgorelosti v poklicu radioloških inženirjev (Starc 2008). V datoteki bfi_izgorelost.sav so zbrani rezultati ankete.

Analiziraj anketo:

predpostavi osnovno hipotezo
1. ali obstajajo razlike med spoloma,
2. ali obstajajo razlike med poklici,
izriši ustrezne grafe za to hipotezo,
izračunaj ustrezno statistiko in preveri statistično značilnost,
komentiraj rezultate.

Postopek reševanja

Podatki ankete morajo v Jamovi biti zapisani tako, da jih lahko obdelamo. Po navadi vsako vprašanje anketnega vprašalnika predstavlja svojo spremenljivko, zato je vsako vprašanje zapisano v svojem stolpcu. Spremenljivke so poimenovane po anketnem vprašanju. Vsaka vrstica predstavlja odgovore enega anketnega vprašalnika. Vsi odgovori anketnega vprašalnika so zapisani kot števila.

Odpremo podatke (Open -> bfi_izgorelost.sav) in ugotovimo, da je v raziskavo vključenih 140 anketnih vprašalnikov. Imena spremenljivk je potrebno urediti, saj jih Jamovi nepravilno prebere. V zavihku Variables ob željeni spremenljivki izberemo Edit in jo ustrezno uredimo.

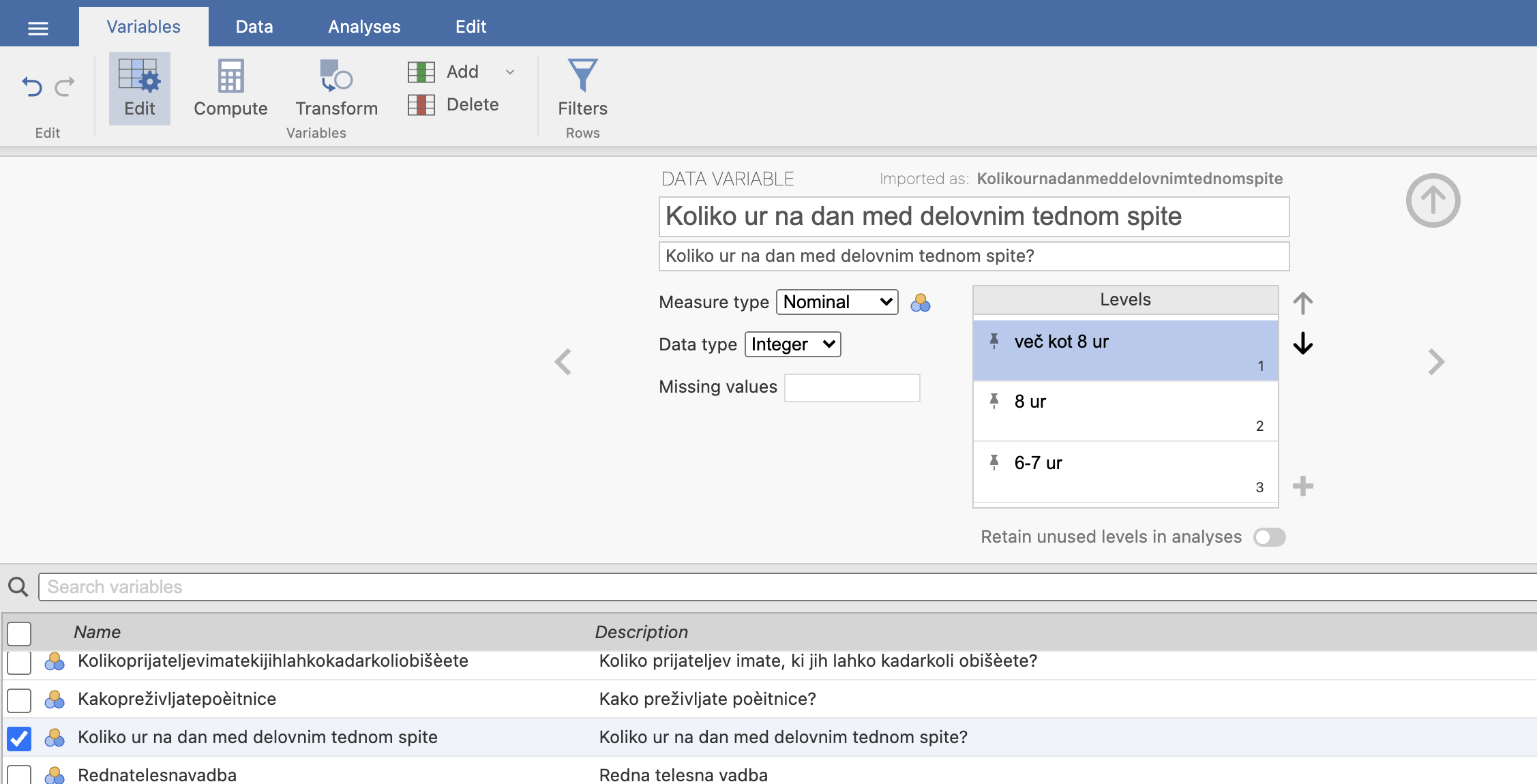
V demografskih vprašanjih imamo podatke o spolu. Imamo 2 kategoriji: moški, ženska. Pri poklicu oziroma delu, ki ga anketiranec opravlja imamo 3 kategorije: inženir ali diplomirani inženir radiologije, mentor kliničnih vaj – delo z bolniki in s študenti radiologije, predavatelj na fakulteti. Na splošno so odgovori na anketna vprašanja po navadi kategorijske spremenljivke.

Analizirali bomo anketno vprašanje 5 in vprašanje 20.

Vprašanje 5: Koliko ur na dan med delovnim tednom običajno spite?

a. 1 več kot 8 ur
b. 2 8 ur
c. 3 6-7 ur
d. 4 manj kot 6 ur

Vprašanje 20: Kako pogosto se počutite utrujeni?

a. 5 vedno
b. 4 pogosto
c. 3 včasih
d. 2 redkokdaj
e. 1 nikoli/skoraj nikoli

Postavili smo si naslednja raziskovalna vprašanja:

V₁: Ali obstajajo statistično značilne razlike v deležih med odgovori na vprašanje »Koliko ur na dan med delovnim tednom običajno spite?« glede na spol?

V₂: Ali obstajajo statistično značilne razlike v deležih med odgovori na vprašanje »Koliko ur na dan med delovnim tednom običajno spite?« glede na poklic?

V₃: Ali obstajajo statistično značilne razlike v deležih med odgovori na vprašanje »Kako pogosto se počutite utrujeni?« glede na spol?

V₄: Ali obstajajo statistično značilne razlike v deležih med odgovori na vprašanje »Kako pogosto se počutite utrujeni?« glede na poklic?

Ker bomo primerjali kategorijske spremenljivke (spol ali poklic) s kategorijskimi spremenljivkami (odgovori na vprašanja) bomo uporabili hi-kvadrat test. Za analizo anket večinoma uporabljamo hi-kvadrat test.

Preverimo 1. vprašanje: Ali obstajajo statistično značilne razlike v deležih med odgovori na vprašanje »Koliko ur na dan med delovnim tednom običajno spite?« glede na spol?

Da bi pokazali razlike med spoloma, kjer imamo štiri odgovore, bomo uporabili stolpični diagram z ukazom Analyses -> Exploration -> Descriptives

Stolpični diagram nam prikaže število ljudi, ki je odgovorilo na vprašanje, hkrati pa prikaže še kako so odgovarjali glede na spol.

Pod možnost Variables izberemo vprašanje Koliko ur na dan med delovnim tednom spite?, pod možnost Split by pa izberemo spremenljivko spol. Za izris stolpičnega diagrama pod zavihkom Plots izberemo možnost Bar plot. Spol (moški, ženske) bo prikazan v dveh različnih barvah. V desnem oknu Results se nam izriše željeni graf.

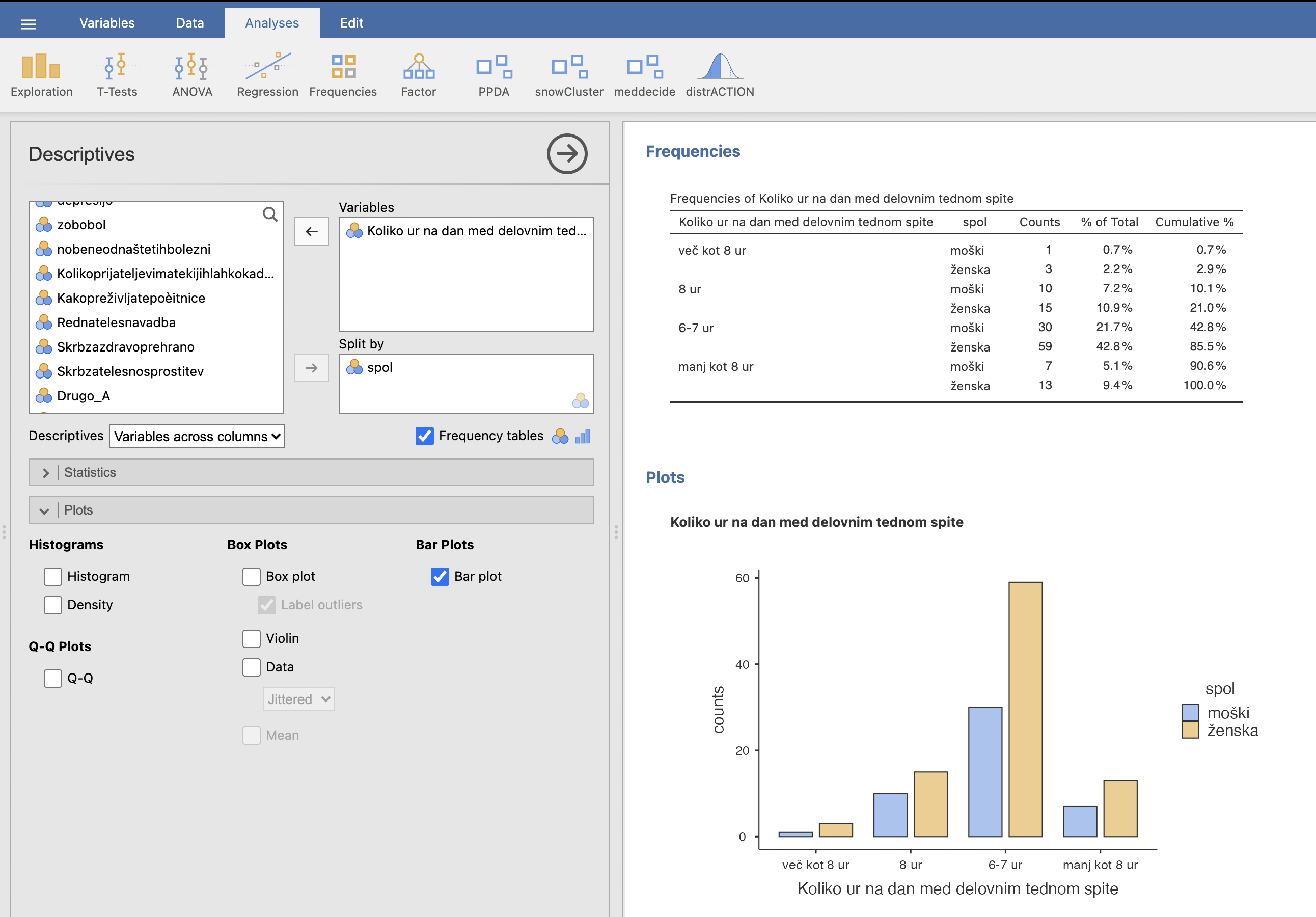
Iz stolpičnega grafa lahko glede na višino stolpcev razberemo, da največ anketirancev med tednom spi 6-7 ur na dan in da je bilo anketiranih več žensk kot moških. Ker so razlike med stolpci pri vsaki kategoriji proporcionalno približno enake, sklepamo, da razlik v količini spanca med spoloma ni.

Ali so deleži odgovorov moških in žensk proporcionalni glede na število ur spanja bomo ugotovili s hi-kvadrat testom.

Uporabimo ukaz: Analyses -> Frequencies in pod Contingency Tables izberemo Independent Samples χ2 test of assosiation. V levem oknu izberemo, da bo spremenljivka Koliko ur na dan med delovnim tednom spite? v kontingenčni tabeli zapisana v stolpcih (Columns), spremenljivka spol pa v vrsticah (Rows). Da bi izračunali hi-kvadrat test, pod razdelkom Statistics označimo Tests: χ2.

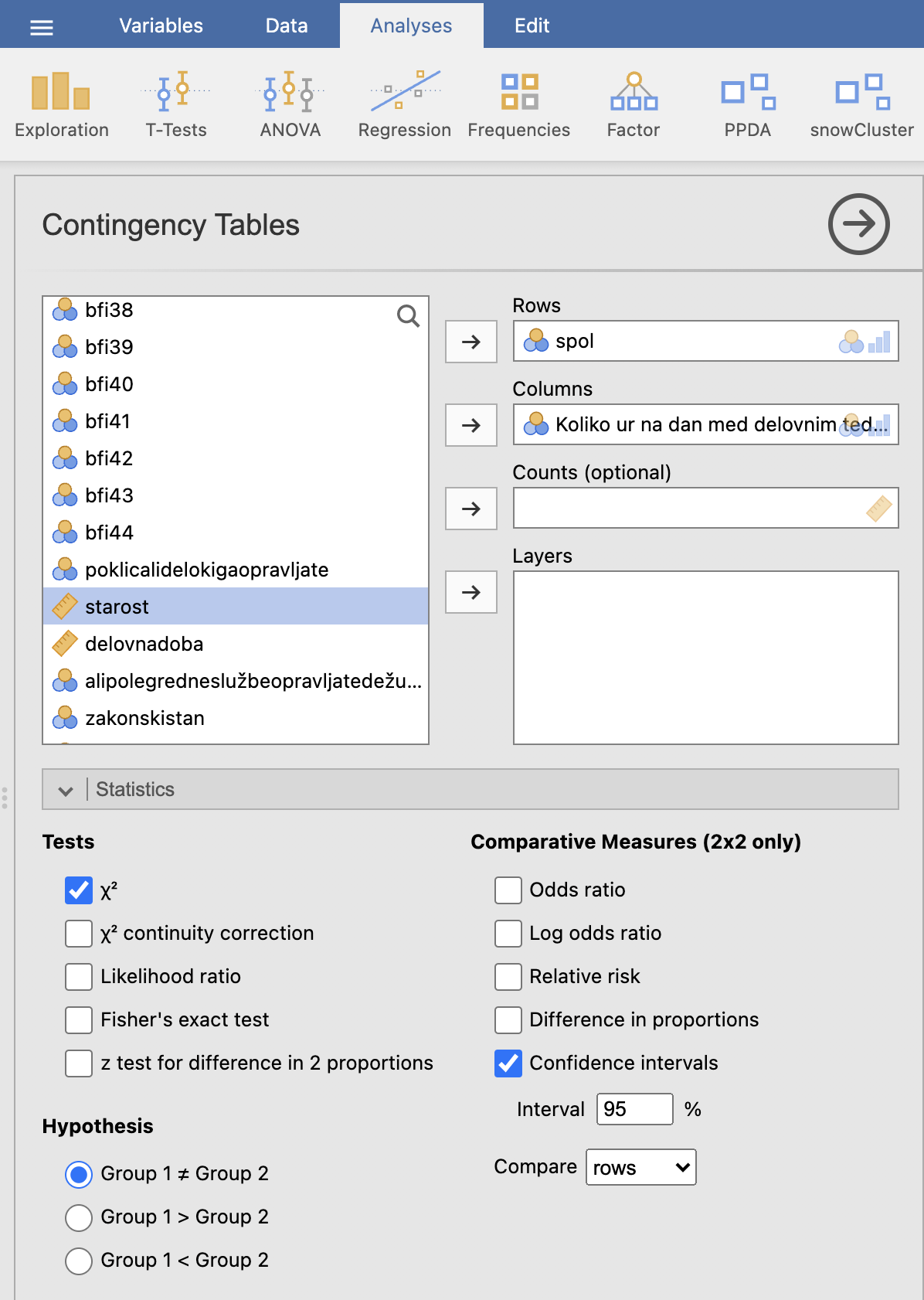
V desnem oknu Results se izpiše kontingenčna tabela, iz katere ugotovimo, da je razmerje med moškimi in ženskami za vsak odgovor približno 1:2.

Izpiše se tudi tabela hi-kvadrat testa.

Hi-kvadrat statistika pravi, da je p-vrednost 0.916, kar pomeni, da glede na število ur spanja, ne obstajajo statistično značilne razlike v deležih med moškimi in ženskami.

Preverimo 2. vprašanje: Ali obstajajo statistično značilne razlike v deležih med odgovori na vprašanje »Koliko ur na dan med delovnim tednom običajno spite?« glede na poklic?

Za izris stolpičnega diagrama uporabimo ukaz Analyses -> Exploration -> Descriptives. Pod možnost Variables izberemo vprašanje Koliko ur na dan med delovnim tednom spite?, pod možnost Split by pa izberemo spremenljivko poklic ali delo, ki ga opravljate. Za izris stolpičnega diagrama pod zavihkom Plots izberemo možnost Bar plot.

V oknu Results se nam izriše graf. Poklic (inž. ali dipl. inž. radiologije, mentor kliničnih vaj – delo z bolniki in s študenti radiologije, predavatelj na fakulteti) je prikazan v treh različnih barvah.

Ugotovimo lahko, da največ anketirancev med delovnim tednom spi 6-7 ur na dan. Največ anketirancev opravlja poklic diplomiranega radiološkega inženirja. Sklepamo, da razlike v številu ur spanja glede na deleže med poklici so, saj razlike med stolpci znotraj enega časa niso proporcionalno enake glede na ostale čase.

Ali so deleži števila ur spanja med delovnim tednom glede na poklic približno enaki, bomo ugotovili s hi-kvadrat testom.

Uporabimo ukaz: Analyses -> Frequencies in pod Contingency Tables izberemo Independent Samples χ2 test of assosiation. V levem oknu izberemo, da bo spremenljivka Koliko ur na dan med delovnim tednom spite? v kontingenčni tabeli zapisana v stolpcih (Columns), spremenljivka poklic ali delo, ki ga opravljate pa v vrsticah (Rows). Da bi izračunali hi-kvadrat test, pod razdelkom Statistics označimo Tests: χ2.

Izpiše se kontingenčna tabela ter tabela hi-kvadrat testa.

Hi-kvadrat statistika pravi, da je p-vrednost 0.550, kar pomeni, da ni statistično značilnih razlik v deležih v številu ur spanja med delovnim tednom, glede na poklic, ki ga opravljajo anketiranci.

Preverimo 3. vprašanje: Ali obstajajo statistično značilne razlike v deležih med odgovori na vprašanje »Kako pogosto se počutite utrujeni?« glede na spol?

Za izris stolpičnega diagrama uporabimo ukaz Analyses -> Exploration -> Descriptives. Pod možnost Variables izberemo vprašanje Kako pogosto se počutite utrujeni?, pod možnost Split by pa izberemo spremenljivko spol. Za izris stolpičnega diagrama pod zavihkom Plots izberemo možnost Bar plot. V desnem oknu Results se nam izriše graf. Spol (moški, ženske) je prikazan v dveh različnih barvah.

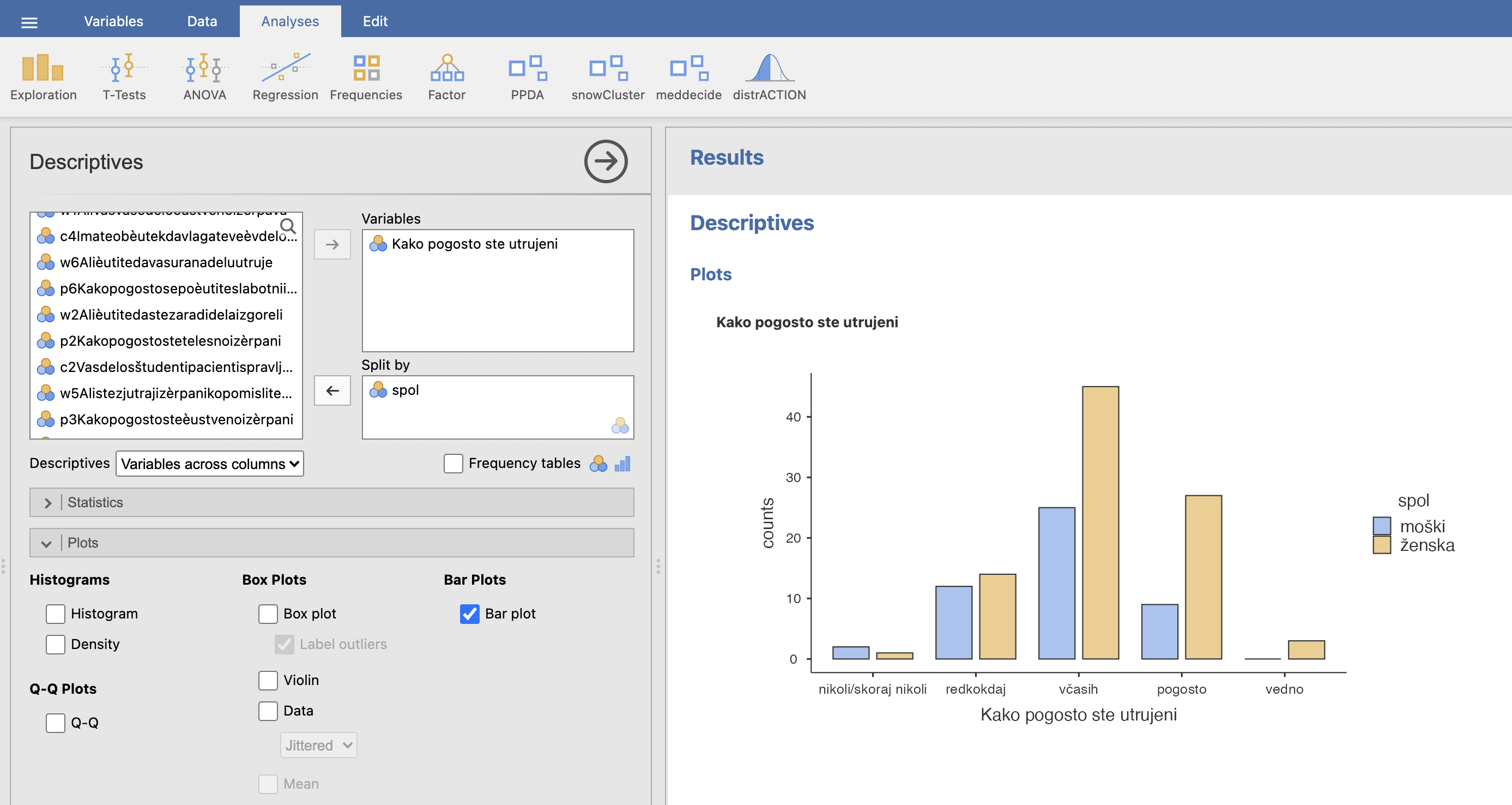
Ugotovimo, da so anketiranci največkrat utrujeni »včasih«. Glede na približno proporcionalno enake razlike med stolpci pri vsakem odgovoru, lahko sklepamo, da razlike v deležih med spoloma ni. Preverimo še s hi-kvadrat testom.

Uporabimo ukaz: Analyses -> Frequencies in pod Contingency Tables izberemo Independent Samples χ2 test of assosiation. V levem oknu izberemo, da bo spremenljivka Kako pogosto ste utrujeni? v kontingenčni tabeli zapisana v stolpcih (Columns), spremenljivka spol pa v vrsticah (Rows). Da bi izračunali hi-kvadrat test, pod razdelkom Statistics označimo Tests: χ2.

V desnem oknu Results se izpiše kontingenčna tabela ter tabela hi-kvadrat testa.

Hi-kvadrat statistika pravi, da je p-vrednost 0.201, kar pomeni, da glede na utrujenost ne obstajajo statistično značilne razlike v deležih med moškimi in ženskami.

Preverimo še 4. vprašanje: Ali obstajajo statistično značilne razlike v deležih med odgovori na vprašanje »Kako pogosto se počutite utrujeni?« glede na poklic?

Za izris stolpičnega diagrama uporabimo ukaz Analyses -> Exploration -> Descriptives. Pod možnost Variables izberemo vprašanje Kako pogosto se počutite utrujeni?, pod možnost Split by pa izberemo spremenljivko poklic ali delo, ki ga opravljate. Za izris stolpičnega diagrama pod zavihkom Plots izberemo možnost Bar plot.

V desnem oknu Results se nam izriše graf. Poklic (inž. ali dipl. inž. radiologije, mentor kliničnih vaj – delo z bolniki in s študenti radiologije, predavatelj na visoki šoli za zdravstvo) je prikazan v treh različnih barvah.

Ugotovimo, da so anketiranci največkrat utrujeni včasih. Glede na približno proporcionalno enake razlike med stolpci znotraj enega odgovora v primerjavi z drugimi odgovori lahko sklepamo, da razlike v deležih med spoloma ni. Preverimo še s hi-kvadrat testom.

Uporabimo ukaz: Analyses -> Frequencies in pod Contingency Tables izberemo Independent Samples χ2 test of assosiation. V levem oknu izberemo, da bo spremenljivka Kako pogosto ste utrujeni? v kontingenčni tabeli zapisana v stolpcih (Columns), spremenljivka poklic ali delo, ki ga opravljate pa v vrsticah (Rows). Da bi izračunali hi-kvadrat test, pod razdelkom Statistics označimo Tests: χ2.

Pod razdelkom Cells izberemo še, katere odstotke bomo izpisali v kontingenčni tabeli. Izberemo odstotke po stolpcih.

V oknu Results se izpiše kontingenčna tabela ter tabela hi-kvadrat testa.

V prvi tabeli lahko vidimo tudi deleže med poklici pri posameznih odgovorih, kjer lahko ugotovimo, da so deleži med poklici različni, vendar hi-kvadrat statistika pravi, da je p-vrednost 0.747, kar pomeni, da glede na utrujenost ne obstajajo statistično značilne razlike v deležih med različnimi poklici.

Končne ugotovitve

Stolpične diagrame uporabljamo za prikazovanje kategorijskih spremenljivk, zato so primerni za prikazovanje odgovorov na anketna vprašanja.

Kontingenčna tabela je tabela frekvenc posameznih dogodkov v vzorcu (štejemo koliko odgovorov imamo pri kombinacijah posameznih kategorij pri več kategorijskih spremenljivkah).

Hi-kvadrat test uporabljamo, kadar želimo preveriti ali so razmerja med količinami enaka glede na neko spremenljivko. Zastavimo ničto hipotezo, ki pravi da sta opazovani kategorijski spremenljivki nepovezani. S hi-kvadrat testom nato primerjamo dejansko število udeležencev po kategorijah s pričakovanim številom udeležencev, če bi imeli enaka razmerja med kategorijami. V primeru, da je p-vrednost manjša od 0.05, zavrnemo ničto hipotezo, kar pomeni, da so deleži ljudi med različnimi kategorijami različni, torej kategorijska spremenljivka statistično značilno vpliva na različne deleže med skupinami.

V našem primeru se ukvarjamo z deležem moških in žensk pri vsakem odgovoru na eno anketno vprašanje. Če so deleži moških in žensk pri vsakem odgovoru približno enaki, potem lahko trdimo, da sta spol in število ur spanja nepovezana, saj je delež moških in žensk pri vsakem odgovoru na anketno vprašanje približno enak. Na enak način razlagamo rezultate drugih spremenljivk.

Tu smo obravnavali samo osnovne analize anketnih vprašanj.

5.4 Testiranje podatkov v deležih – odvisne meritve

Navodila vaje

V datoteki HeartValve_pre_post.xlsx so zbrani podatki o stanju pacientov po menjavi srčne zaklopke (Marques De Sá 2007).

Zanima nas stanje pacientov pred in po menjavi srčne zaklopke (PRE_C, POST_C), ki je ovrednoteno po standardu NYHA: (NYHA – New York Heart Association):

0 = No symptoms
1, 2 = Mild symptoms
3, 4 = Severe symptoms
Ali se je stanje pacientov bistveno izboljšalo?
1. Izvedi ustrezno statistično analizo in podaj komentarje.

Postopek reševanja

Z Jamovi preberemo podatke iz naloge za statistično analizo. Izberemo Open in odpremo ustrezno Excelovo datoteko HeartValve_pre_post.xlsx.

Podatki so organizirani tako, kot je prikazano v spodnji tabeli:

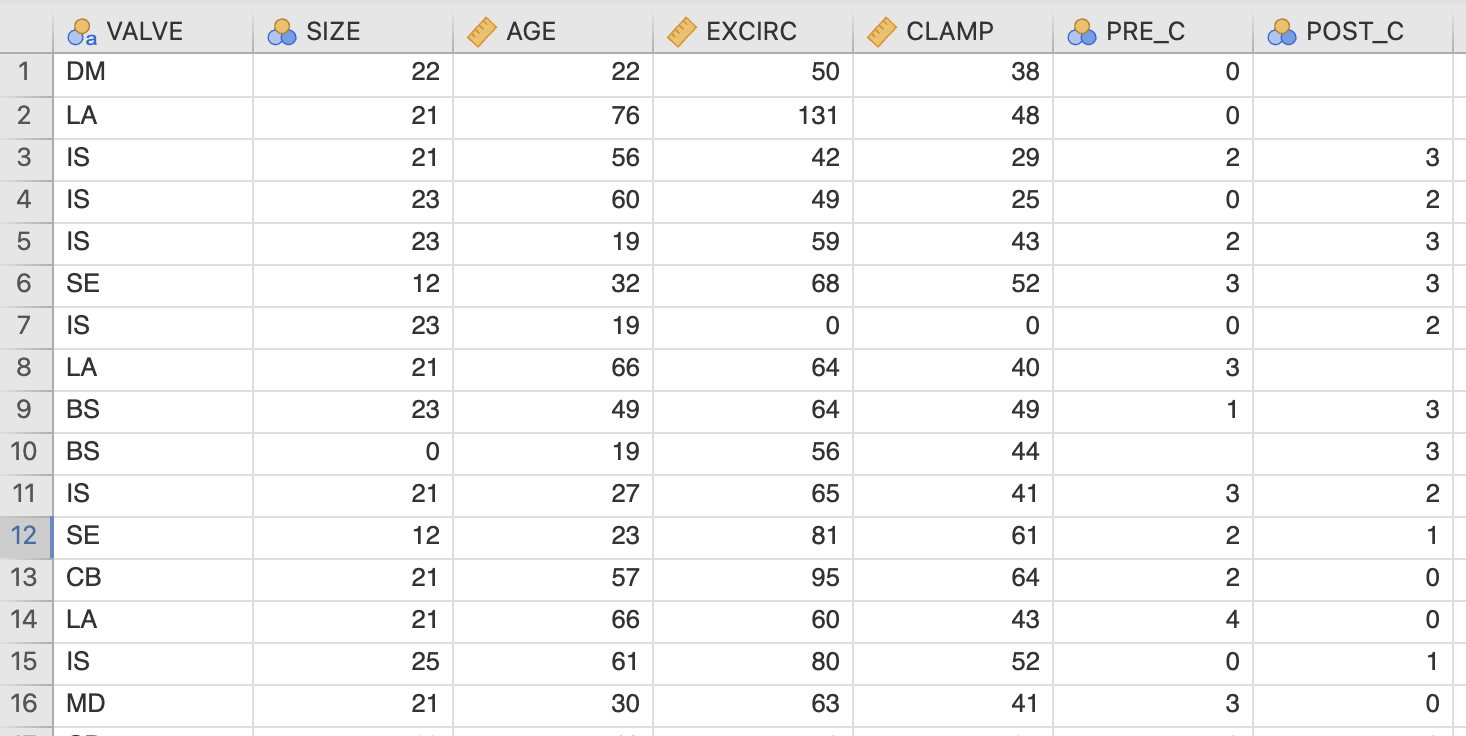
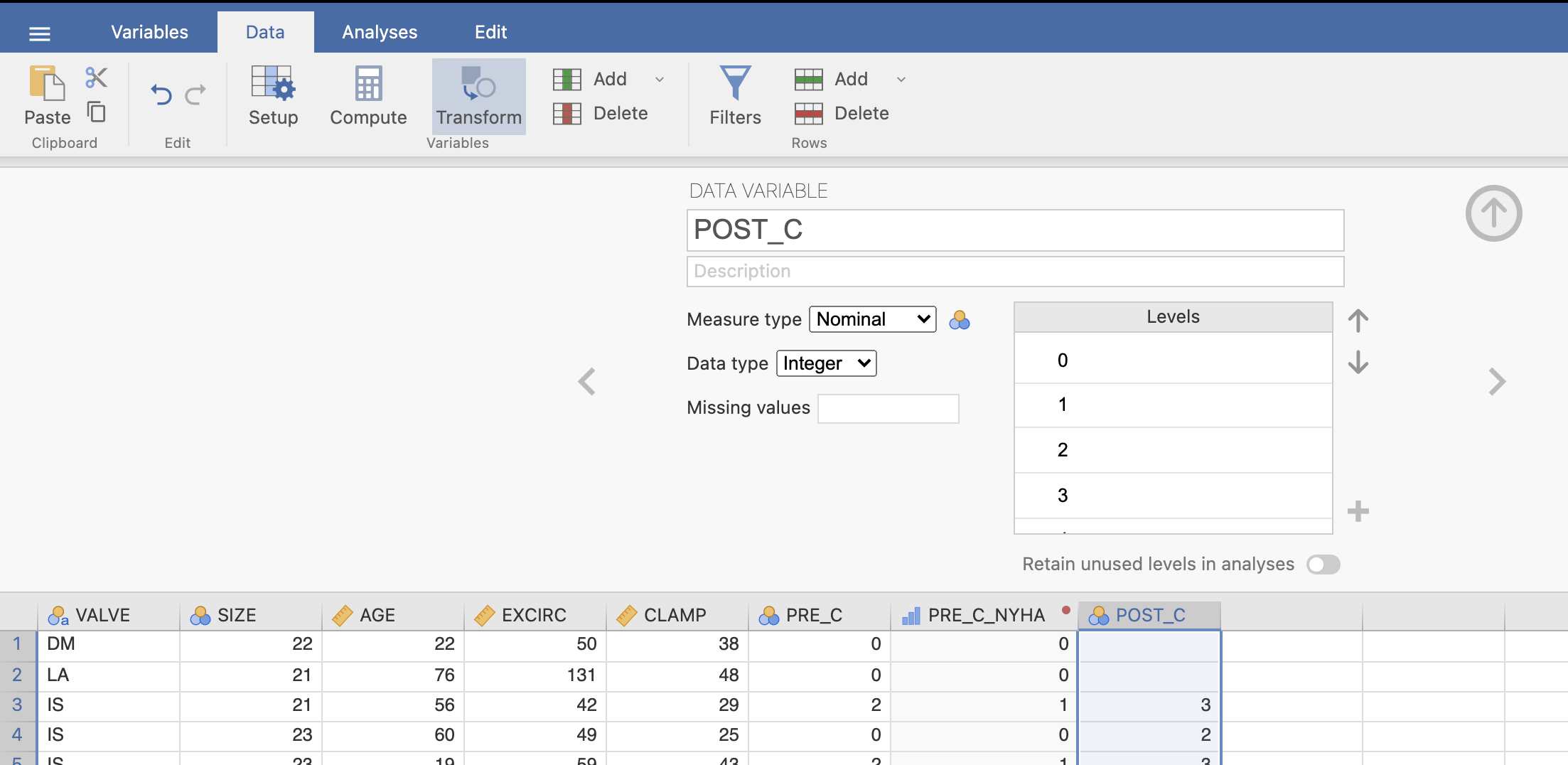
Obravnavamo 526 pacientov, ki so imeli zamenjavo srčne zaklopke (nekatere vrednosti manjkajo, tako da imamo v resnici manj meritev). Ker nas zanima stanje pacientov ovrednoteno po standardu NYHA pred in po menjavi srčne zaklopke, obravnavamo spremenljivki PRE_C in POST_C. To sta kategorijski spremenljivki z vrednostmi: 0, 1, 2, 3, 4.

Po označbah NYHA to predstavlja naslednje kategorije pacientov: 0 = No symptoms; 1 in 2 = Mild symptoms; 3 in 4 = Severe symptoms. Zato najprej preoblikujemo spremenljivke v NYHA označbe po naslednjem postopku. Z izbiro spremenljivke PRE_C in ukazom Transform bomo prekodirali spremenljivko PRE_C glede na NYHA označbe.

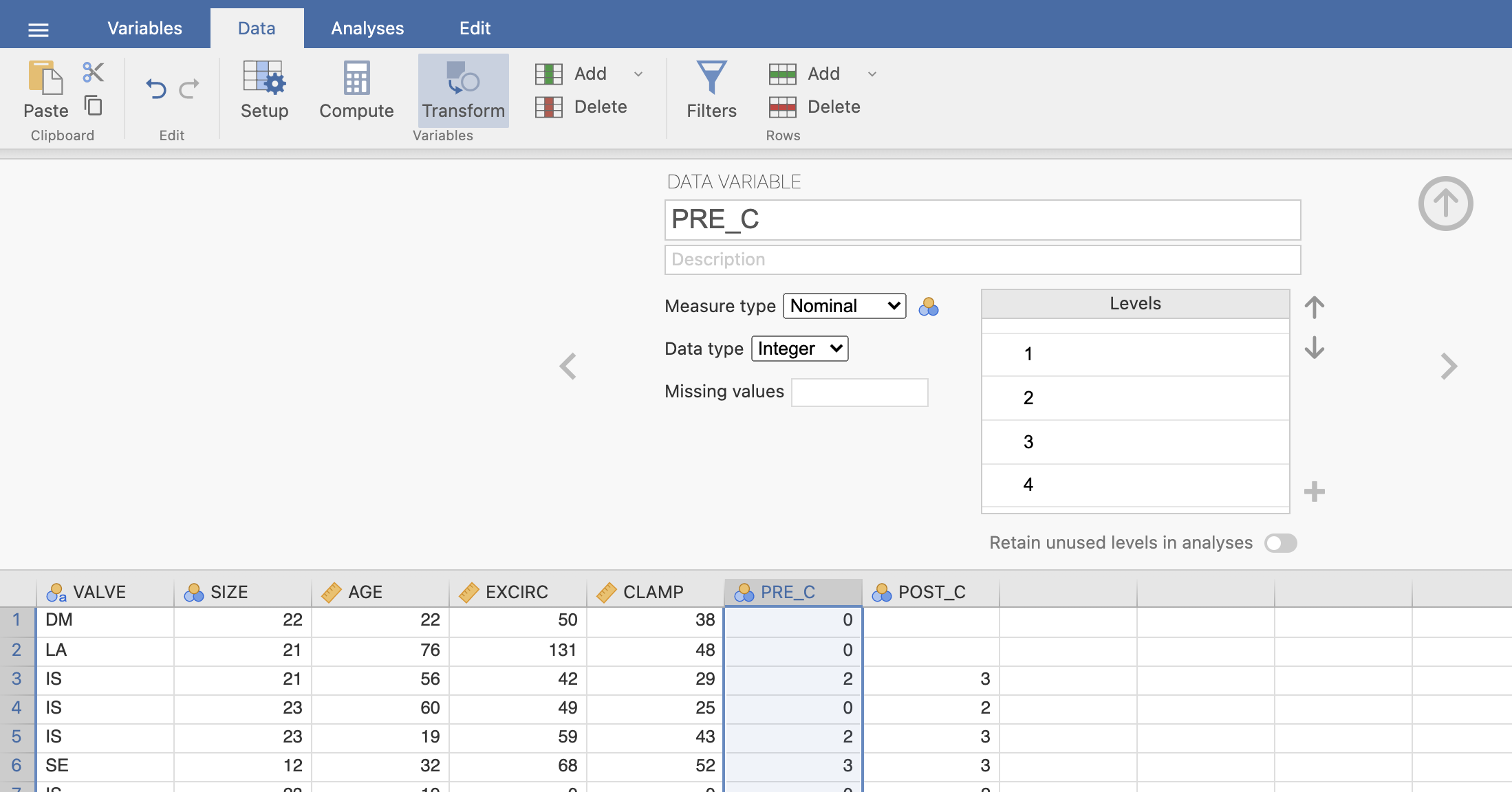
V oknu Transformed variable poimenujemo novo spremenljivko PRE_C_NYHA, kot Source variable izberemo spremenljivko PRE_C in pod using transform izberemo Create New Transform ….

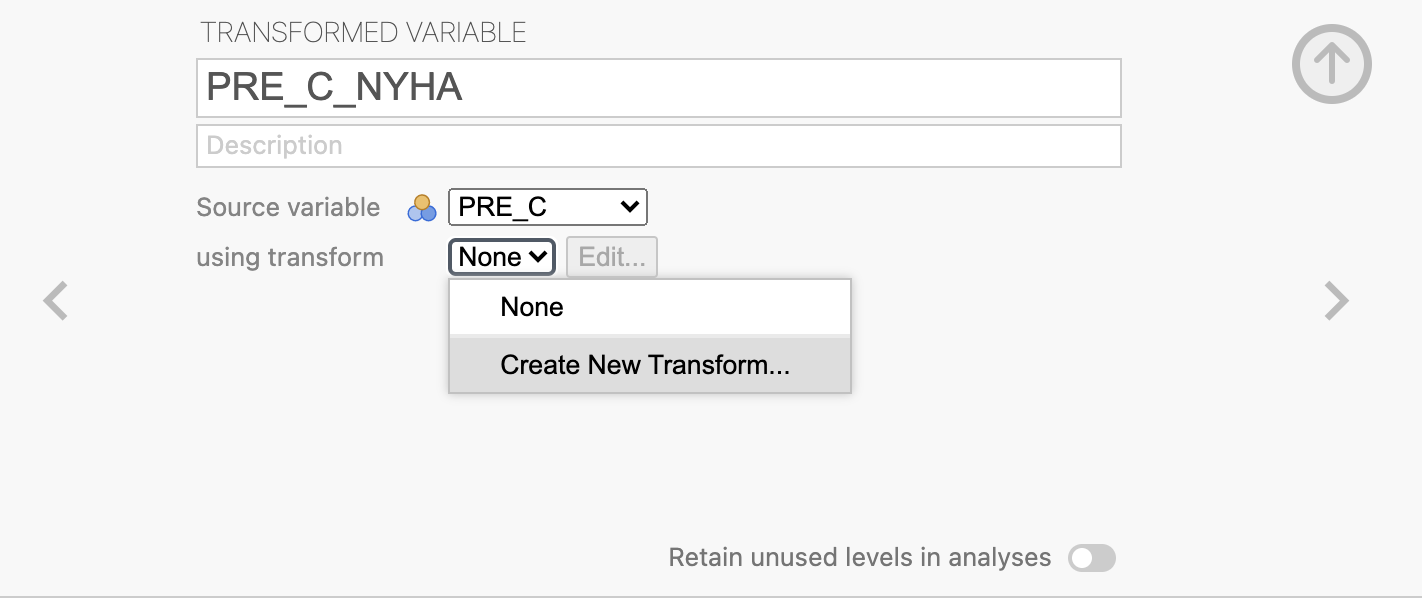
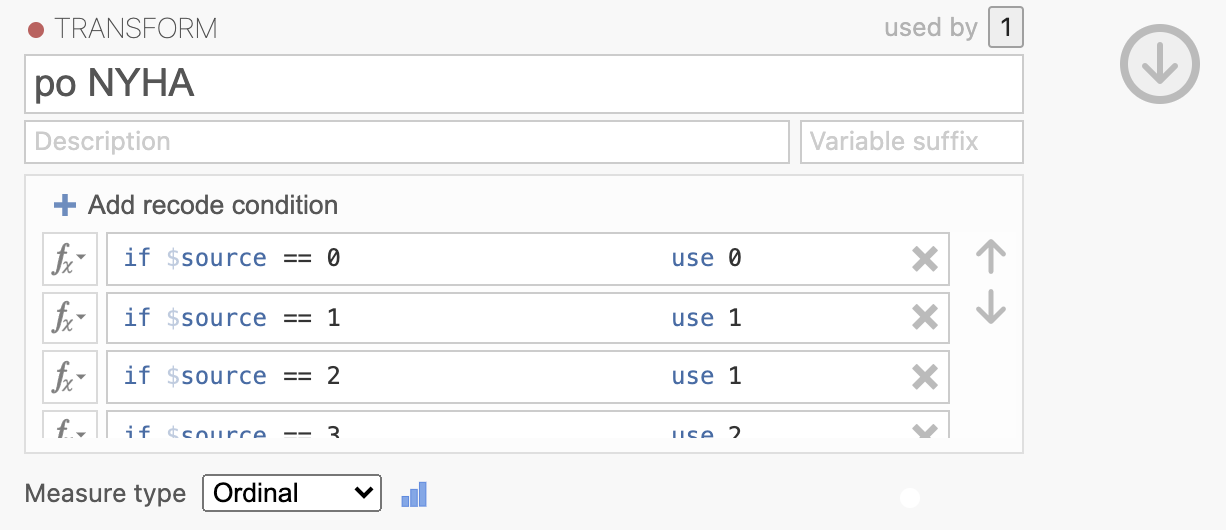
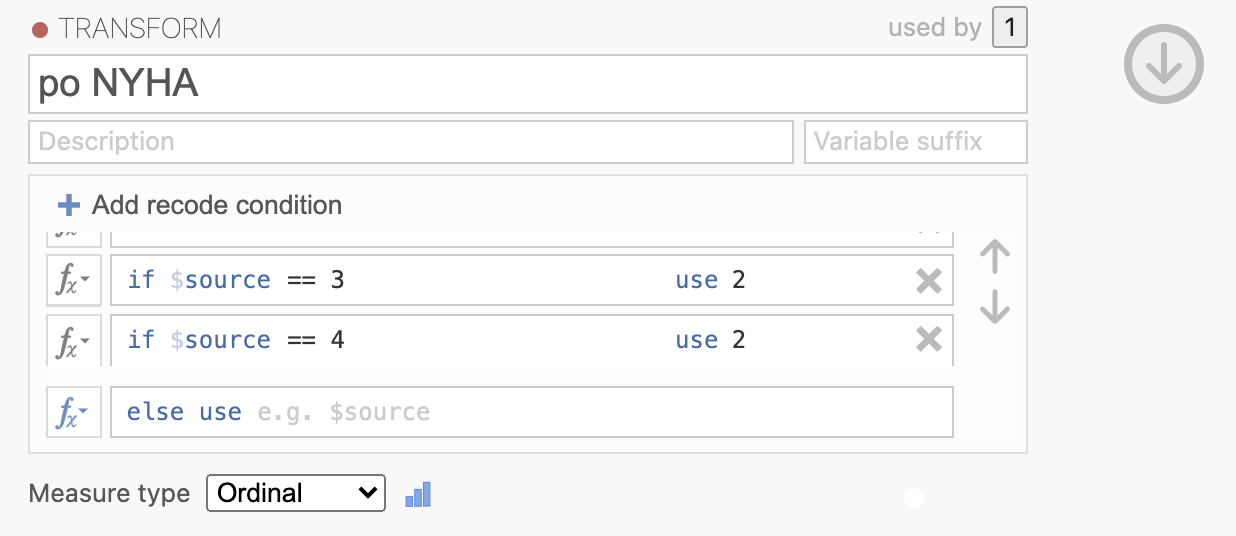
Poimenujemo novo kodiranje z imenom po NYHA in z gumbom Add recode condition določimo, kako se bodo vrednosti kodirale in sicer 0 -> 0, 1 -> 1 in 2 -> 1 ter 3 -> 2 in 4 -> 2, pri čemer predpostavimo, da nove vrednosti predstavljajo: 0 = No Symptoms, 1 = Mild Symptoms, 2 = Severe Symptoms po NYHA.

Podobno prekodiramo spremenljivko POST_C v novo spremenljivko POST_C_NYHA. Z izbiro spremenljivke POST_C in ukazom Transform bomo prekodirali spremenljivko POST_C glede na NYHA označbe.

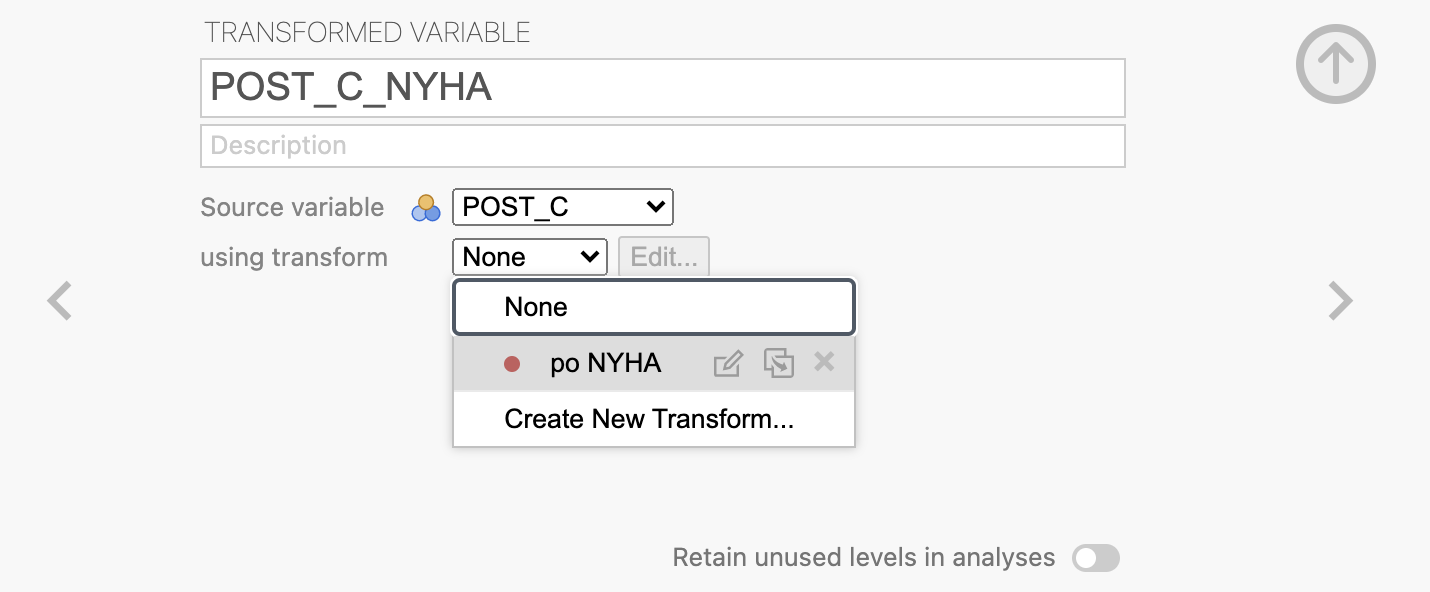
V oknu Transformed variable poimenujemo novo spremenljivko POST_C_NYHA, kot Source variable izberemo spremenljivko POST_C in pod using transform izberemo že ustvarjeno kodiranje po NYHA.

Ker bi radi pokazali, ali so se kategorije bolečin po NYHA pri istih pacientih po operaciji spremenile glede na stanje pred operacijo in ker imamo kategorijske spremenljivke, bomo uporabili McNemarjev test, s katerim testiramo spremembe deležev kategorijskih spremenljivk z odvisnimi meritvami.

Izvedemo ukaz Analyses -> Frequencies in pod Contingency Tables izberemo Paired samples - McNemar test.

V levem oknu Paired Samples Contingency Tables izberemo spremenljivko PRE_C_NYHA v vrstice (Rows) in spremenljivko POST_C_NYHA v stolpce (Columns). V desnem oknu Results se nam izpiše kontingenčna tabela in tabela s statistiko McNemar testa.

Končne ugotovitve

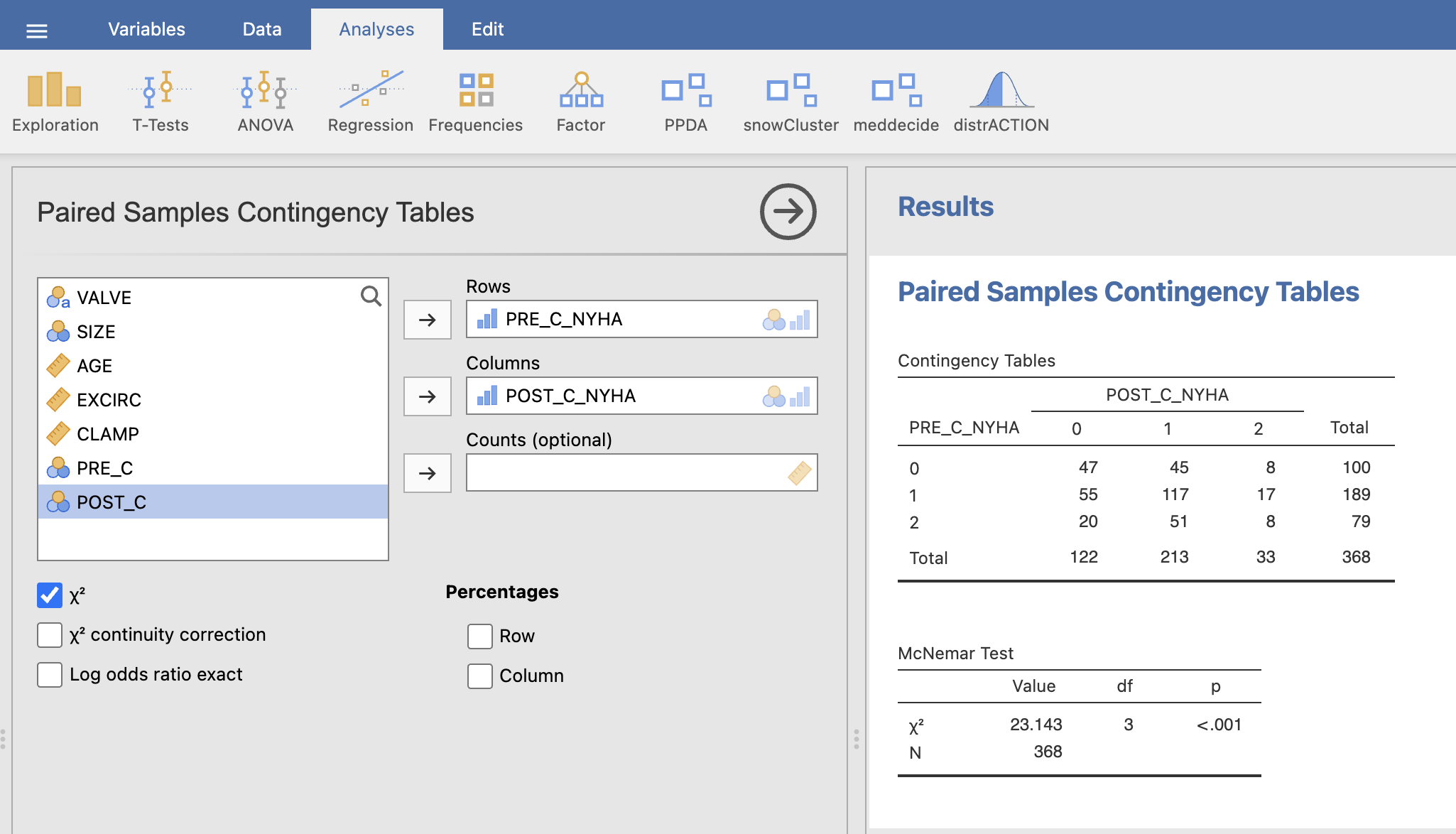
Iz rezultatov statistične analize lahko ugotovimo, da so se deleži pacientov glede na stopnje bolečin pred in po operaciji statistično značilno spremenili (p < 0.001).

Iz kontingenčne tabele tudi opazimo premike pacientov predvsem iz stopenj 1 in 2 po NYHA v nižje stopnje, s čimer lahko ugotovimo, da se stanje pacientov po operaciji srčne zaklopke v splošnem izboljša.

5.5 Enosmerna ANOVA

Navodila vaje

V datoteki Breast Tissue.xls so zbrane meritve impedančne spektroskopije na različnih tkivih dojke po biopsiji (Estrela da Silva et al. 2000).

Ugotovi, ali se meritve različno odzivajo glede na vrste tkiva.

Najprej izvedi ANOVA za posamezne meritve glede na vrste tkiv, potem pa še Post-Hoc analizo.
Analizo opremi z ustreznimi grafi in opisnimi statistikami.
Komentiraj rezultate.

Postopek reševanja

V Jamovi odpremo podatke iz naloge za statistično analizo. Izberemo Open in odpremo ustrezno Excelovo datoteko Breast Tissue.xlsx.

Opazimo, da vrstice 107-110 za našo analizo niso relevantne, zato jih označimo in izbrišemo. Kako izbrišemo vrstice, si lahko ogledate v nalogi pog. 5.1.

V prvem stolpcu so kot spremenljivka Class zapisane vrste tkiv, v ostalih stolpcih pa so zbrane meritve pacientov pridobljene z impedančno spektroskopijo meritev I0, PA500, HFS, DA, AREA… V nalogi se sprašujemo, ali se meritve različno odzivajo glede na vrste tkiva.

V tej nalogi se bomo ukvarjali z meritvijo I0.

Sprašujemo se, ali se meritve I0 različno odzivajo glede na vrste tkiva oziroma z drugimi besedami, ali je tkivo statistično pomemben faktor za meritev I0. Da odgovorimo na to vprašanje, moramo narediti analizo enosmerne ANOVA.

Za ostale meritve je postopek analize podoben. Zato bomo v nadaljevanju naredili analizo samo za spremenljivko I0.

Spremenljivka X predstavlja tkiva (Class), kjer imamo na voljo 6 tkiv (6 kategorij). Spremenljivka X je kategorijska spremenljivka in predstavlja faktor v naši analizi. Spremenljivka Y predstavlja skalarno meritev impedančne spektroskopije (meritve I0). Spremenljivka Y je skalarna spremenljivka in predstavlja odzivno spremenljivko v naši analizi.

Ker imamo faktor z več kot dvema stopnjema, uporabimo enosmerno ANOVO.

Pri risanju ANOVE rišemo graf okvir z ročaji (ang. boxplot). Graf prikazuje porazdelitev skalarnih spremenljivk.

Narišemo boxplot z ukazom Analyses -> Exploration -> Descriptives in izpolnimo okno Descriptives kot je prikazano na spodnji sliki. Pod razdelkom Plots označimo izris grafa Box plot. Primerjali bomo meritve I0 glede na spremenljivko Class.

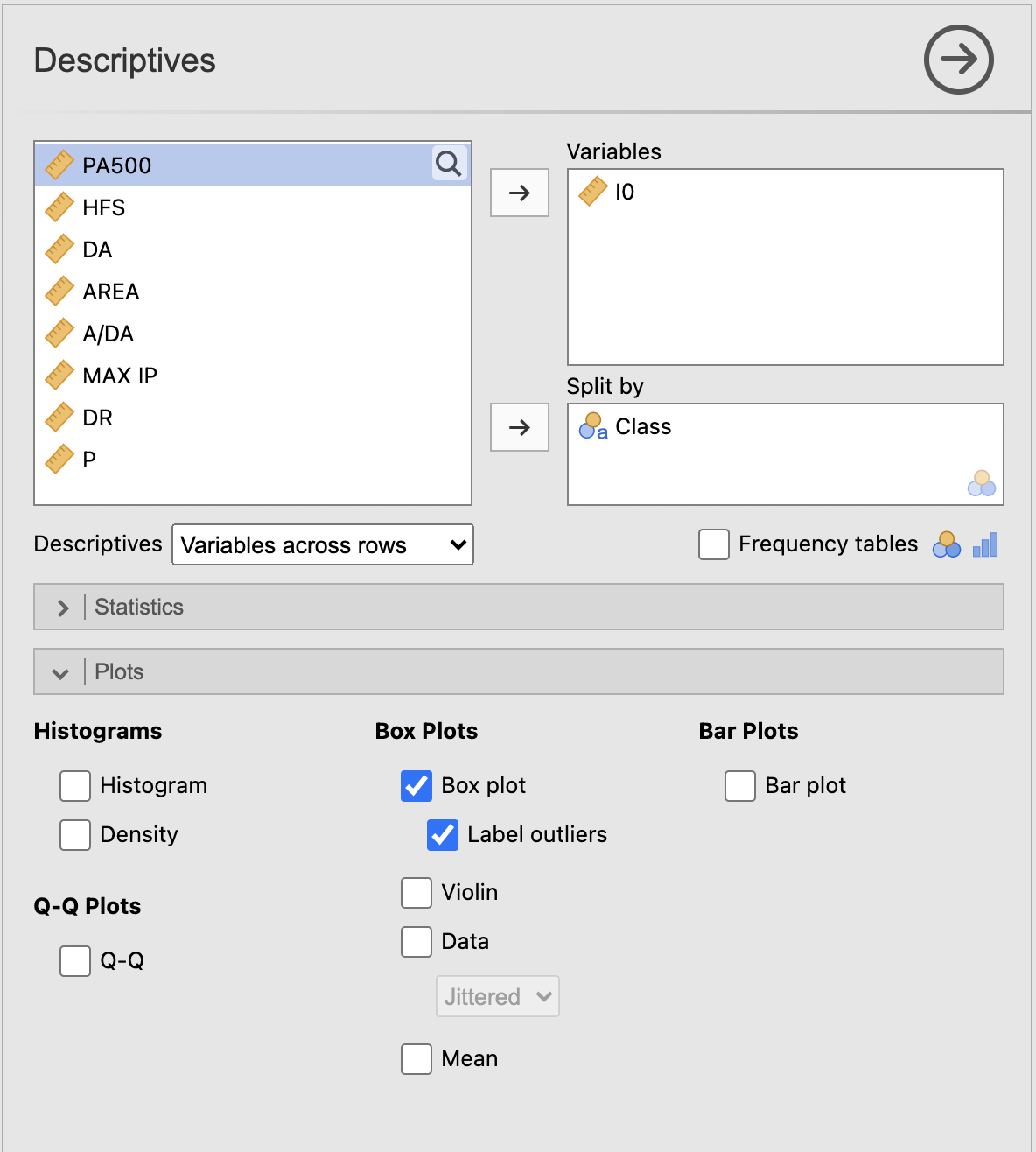
V oknu Results se izriše graf okvir z ročajem.

Pri tipu tkiva ADI in CON imamo zelo visoke vrednosti, medtem ko so vrednosti pri tipih tkiva CAR, FAD, GLA, MAS podobne. Če mediana boxplota ne seka 1. ali 3. kvartila drugega boxplota, obstaja statistično značilna razlika med dvema tkivoma, zato lahko ugotovimo, da se ADI statistično značilno razlikuje od vseh ostalih tkiv. Enako velja za tkivo CON. Tkiva FAD, GLA in MAS se na pogled med seboj statistično značilno ne razlikujejo. Iz grafov lahko ugotovimo, da meritve I0 zelo dobro ločujejo med tkivi, zato je I0 pomemben faktor za ločevanje med tkivi. Prav tako lahko zelo dobro ugotovimo, katera tkiva boljše ločuje od drugih.

Izvedemo ANOVO: Analyses -> ANOVA -> ANOVA.

Pod Dependent Variables izberemo spremenljivko I0, pod Fixed Factors pa spremenljivko Class.

V desnem oknu Results se izpiše naslednja tabela.

Na podlagi analize variance smo ugotovili, da je I0 statistično pomemben faktor za ločevanje med tkivi (p < 0.001). F-statistika je 216.345, kar je visoka vrednost in zaradi tega imamo veliko statistično značilnost oziroma zelo malo p-vrednost.

Da bi ugotovili, med katerimi tkivi meritev I0 dobro ločuje (obstaja statistično značilna razlika) naredimo še Post-Hoc analizo.

Pod razdelkom Post Hoc Tests izberemo naš faktor primerjave Class in označimo Tukey. Kriterij Tukey izberemo, kadar imamo več kot 5 primerjav.

Izriše se Post Hoc tabela, ki je prikazana spodaj.

Post hoc tabela nam prikaže, katera tkiva se med seboj statistično značilno razlikujejo. Iz tabele je razvidno, da se ADI statistično značilno razlikuje od vseh ostalih tkiv (p < 0.001). Ugotovimo lahko, da je razlika v spremenljivki I0 med ADI in ostalimi tkivi vedno pozitivna, kar pomeni, da ADI statistično značilno odstopa po meritvah I0 navzgor. Prav tako lahko za tkivo CON ugotovimo, da se statistično značilno razlikuje od ostalih tkiv po meritvah I0 (p < 0.001), in sicer ima nižje vrednosti kot ADI, vendar višje vrednosti od vseh ostalih tkiv. Ostala tkiva se po meritvah I0 statistično značilno ne razlikujejo (p > 0.05)

Enak postopek ponovimo še za vse ostale meritve.

Končne ugotovitve

Z analizo variance smo ugotovili, da se meritev I0 statistično različno odziva glede na vrste tkiva oziroma, da je vrsta tkiva statistično značilen faktor za meritev I0 (F = 216.345, p < 0.001).

Po dodatni post hoc analizi smo ugotovili, da se meritve I0 statistično značilno razlikujejo pri tkivu ADI od vseh ostalih tkiv, kjer smo ugotovili višje vrednosti I0 pri tkivu ADI od vseh ostalih tkiv. Podobno lahko ugotovimo, da se meritve I0 statistično značilno razlikujejo tudi pri tkivu CON od vseh ostalih tkiv, pri čemer so vrednosti I0 pri tem tkivu nižje kot pri tkivu ADI in višje od ostalih tkiv. Ostala tkiva se z meritvami I0 statistično značilno ne razlikujejo.

Na podoben način lahko izvedemo statistično analizo pri ostalih meritvah. Ugotovimo, da je vrsta tkiva statistično pomemben faktor tudi pri meritvah PA500, HFS, DA, AREA, ADA, MAXIP, DR in P (p < 0.001). Dodatno je potrebno narediti še post hoc analizo, da ugotovimo, pri katerih vrstah tkiva se meritve statistično značilno med seboj razlikujejo.

5.6 Enosmerna ANOVA na ponovljivih meritvah

Navodila vaje

V Jamovi odprite datoteko kreatinin_akin_time_meas.sav. V datoteki imamo podatke o meritvah kreatinina pred operacijo (Kališnik et al. 2017), takoj po operaciji ter 2h, 24h in 48h po operaciji za paciente, ki so razvili akutno motnjo delovanja ledvic in za tiste, ki nimajo motnje delovanja ledvic (AKIN = 0 nimajo motnje, AKIN = 1 imajo motnjo delovanja ledvic).

Nariši grafe povprečja vrednosti kreatinina po vseh meritvah glede na AKIN.
Z analizo variance analiziraj spremembe kreatinina pri pacientih z AKIN = 0.
Z analizo variance analiziraj spremembe kreatinina pri pacientih z AKIN = 1.
Kaj lahko ugotoviš?
Po kateri meritvi se lahko ugotovi, ali gre za statistično značilne spremembe v vrednostih kreatinina pri pacientih z AKIN = 1?
Ali lahko trdimo, da se bo že po 2h lahko ugotovilo, ali bo razvil pacient akutno vnetje ledvic ali ne?

Postopek reševanja

V datoteki kreatinin_akin_time_meas.sav imamo zbrane meritve spremenljivke kreatinin ob različnih časih pri istih pacientih. Ugotovili bi radi, ali obstajajo statistično značilne razlike med meritvami po času.

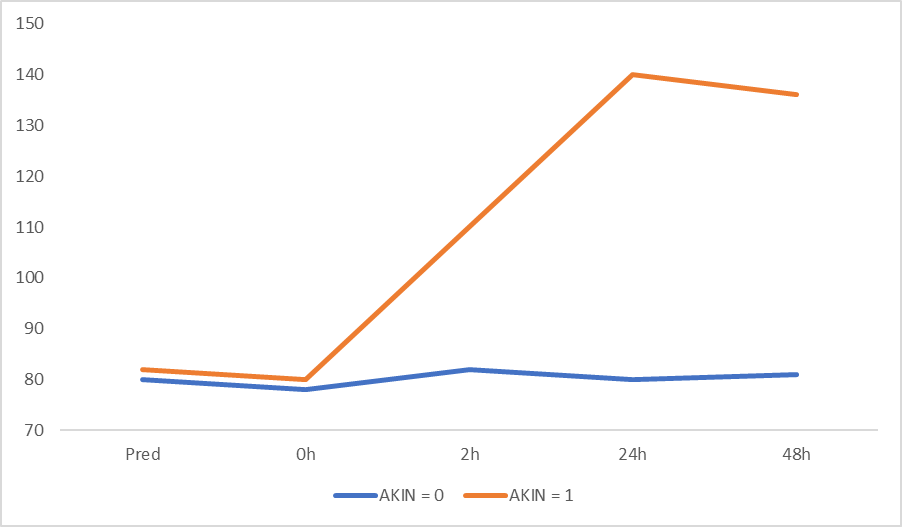
Graf 1: Kreatinin ob različnih časih pri pacientih z okvaro delovanja ledvic (AKIN = 1) in brez okvare (AKIN = 0).

Graf nam prikazuje kakšne poteke meritev kreatinina lahko pričakujemo glede na čas pri pacientih brez okvare delovanja ledvic (AKIN = 0) in pri pacientih z okvaro delovanja ledvic (AKIN = 1). Zanima nas, ali lahko na podlagi časovnih meritev kreatinina določimo, ali bo pacient zbolel.

Postavimo si naslednji dve vprašanji:

Ali obstajajo razlike v kreatininu po času pri skupini pacientov brez okvare delovanja ledvic?
Ali obstajajo razlike v kreatininu po času pri skupini pacientov z okvaro delovanja ledvic?

Odpremo datoteko Open -> kreatinin_akin_time_meas.sav.

V Data in v Variables preverimo, ali so podatki pravilno prebrani. Slika prikazuje izsek datoteke s podatki.

Podatke bomo obdelovali posebej za skupino pacientov brez okvare (AKIN = 0) in posebej za skupino pacientov z okvaro delovanja ledvic (AKIN = 1). V programu Jamovi bomo obravnavo teh dveh skupin izvedli ločeno z uporabo ustreznega filtra - izberemo možnost Filters.

V odprtem oknu ustrezno določimo, da bomo obravnavali le paciente brez okvare delovanja ledvic (AKIN = 0). V zavihku Data se nam izpiše novi stolpec, ki označuje, katere podatke bomo uporabili za analizo.

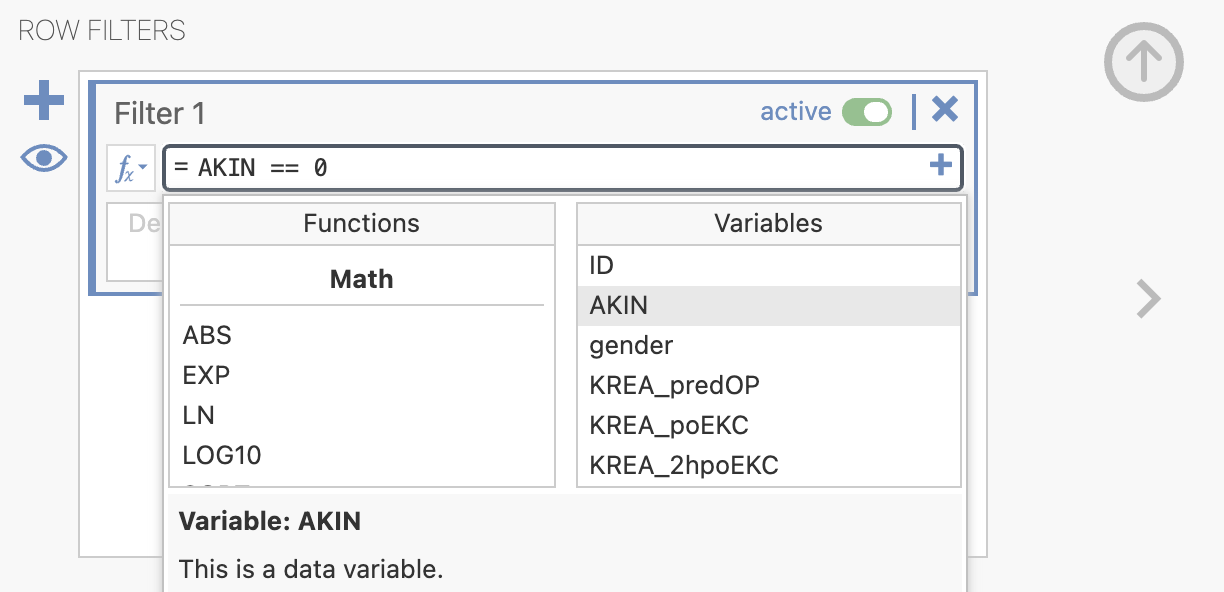
Iz podatkov opazimo, da imamo samo eno spremenljivko kreatinin, vendar je merjena ob različnih časih. Vrednosti po posameznih časih so zapisane v stolpcih, vrstica predstavlja enega pacienta. Podatke bi lahko imeli organizirane tudi drugače, da bi imeli spremenljivko kreatinin in spremenljivko čas, kjer bi označevali v katerem času, smo pridobili meritev kreatinina. Običajna praksa v zdravstvu je, da ena vrstica predstavlja meritve enega pacienta.

Izvedimo ANOVO s ponovljivimi meritvami za obe skupini pacientov posebej, da bomo ugotovili, ali je čas res statistično pomemben faktor za ločevanje med kreatininom. Ker imamo odvisne meritve in 5 vzorcev, bomo za ugotavljanje statistično značilnih razlik uporabili omenjeni test z ukazom: Analyses -> ANOVA -> Repeated Measures ANOVA.

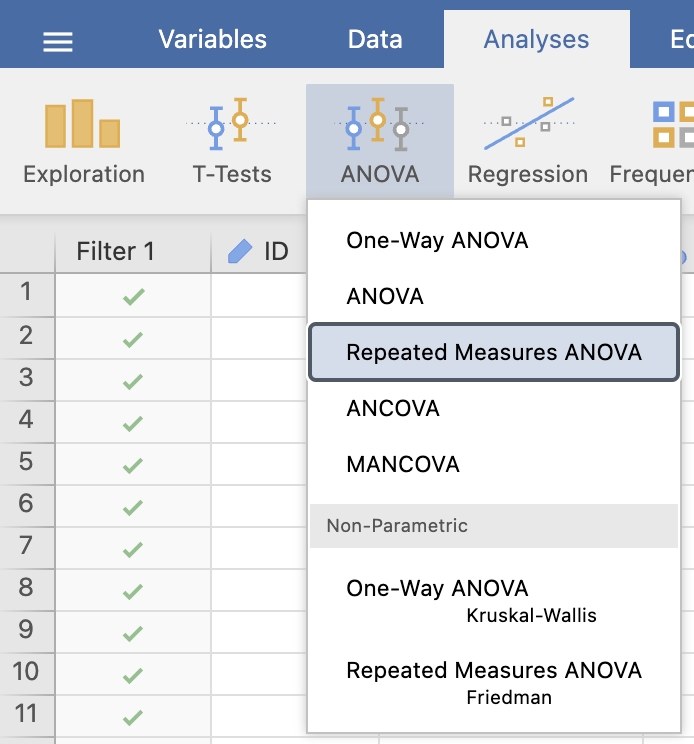
Definiramo ime faktorja tako, da v Repeated Measures Factors namesto RM Factor 1 zapišemo Čas. Določimo število meritev (levelov), ki je enako 5, jih pravilno poimenujemo in vstavimo spremenljivke pod Repeated Measures Cells.

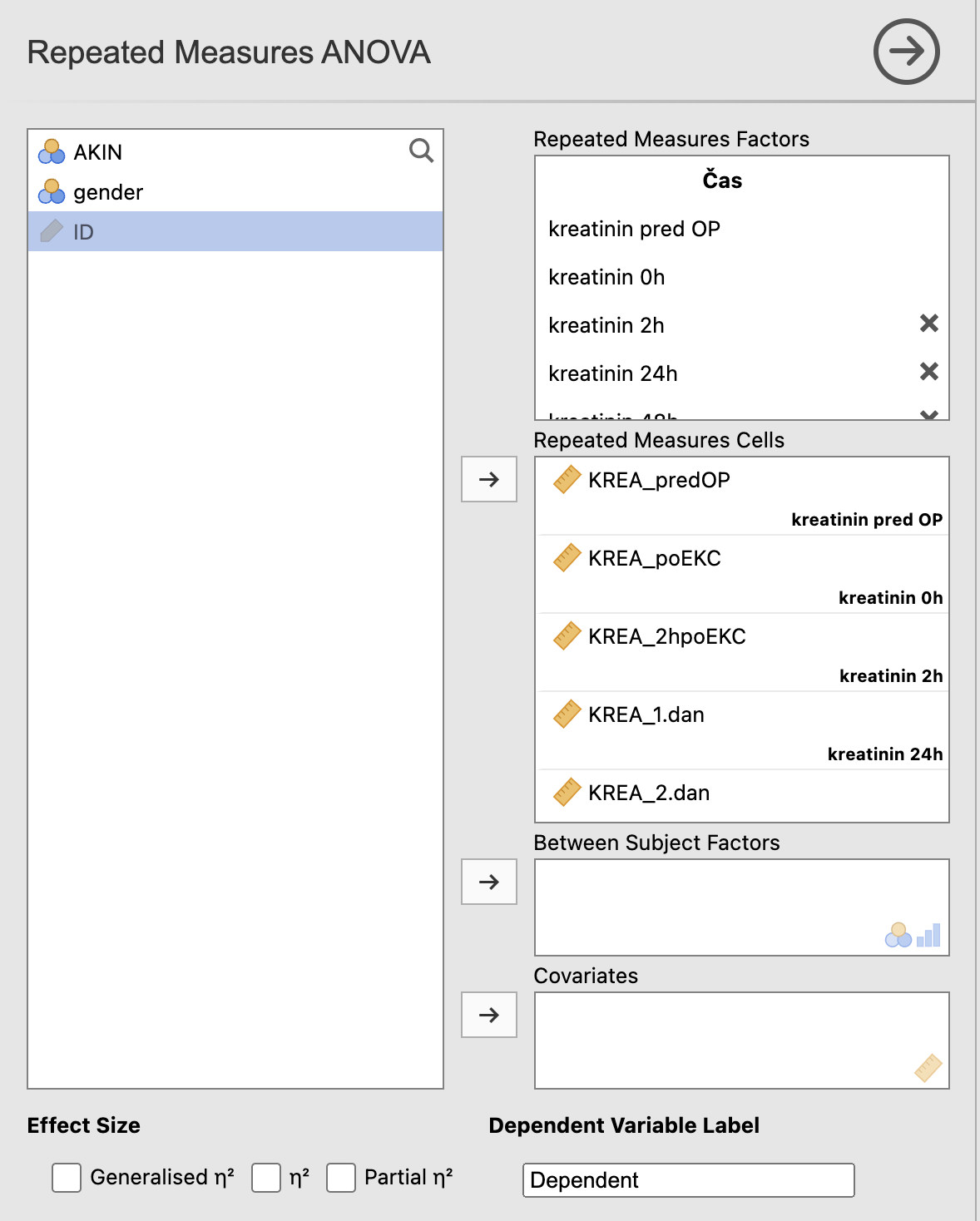
Pod razdelkom Assumption Checks označimo Sphericity tests in izberemo dve vrsti Sphericity corrections: None in Greenhouse-Geisser. Pod razdelkom Post Hoc Tests pa izvedemo post hoc analizo tako, da vstavimo čas kot opazovano spremenljivko in označimo kriterij Tukey, ker imamo več kot 5 primerjav.

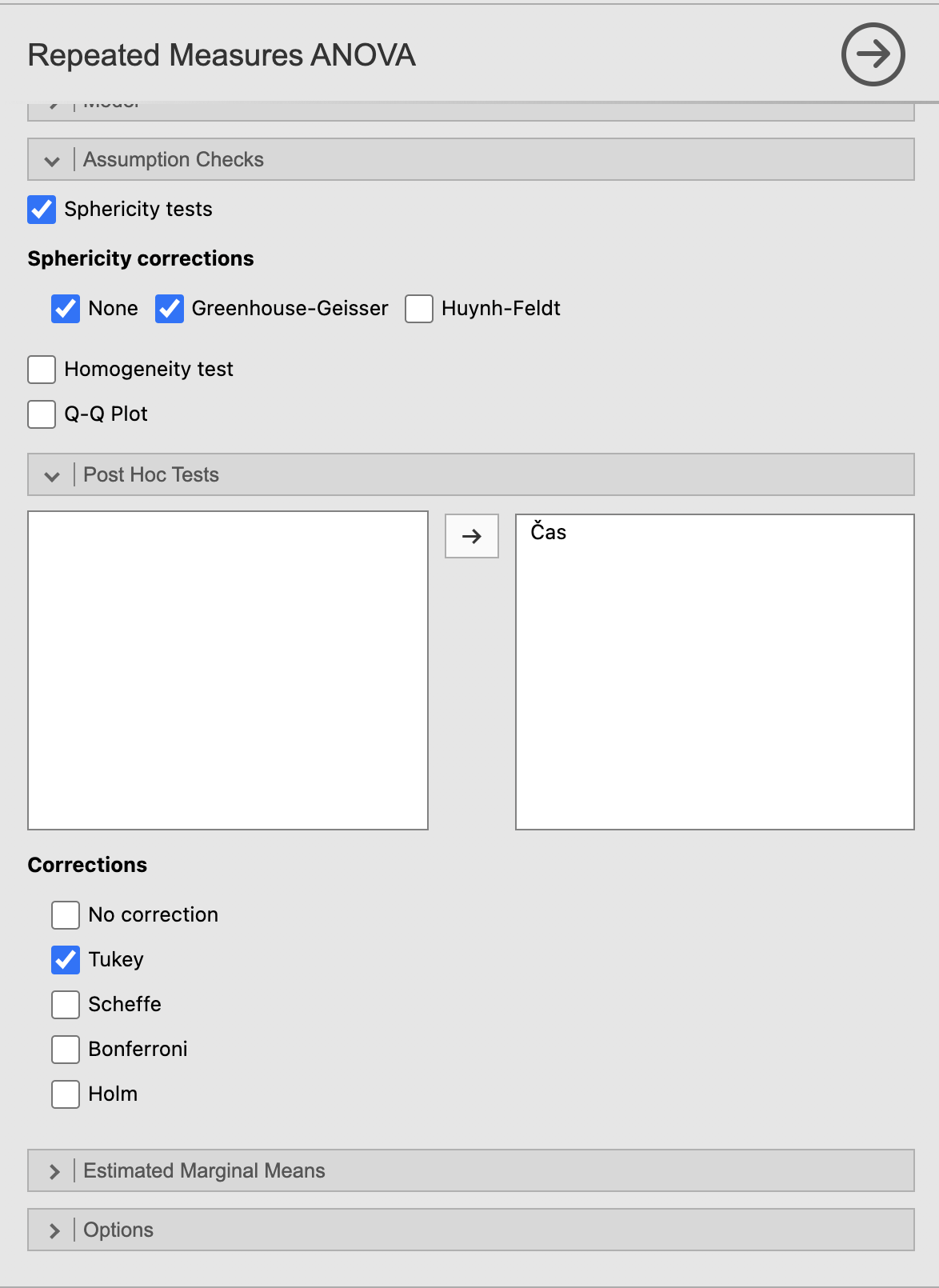
Za izris grafov povprečja vrednosti kreatinina po vseh meritvah glede na AKIN = 0 pod razdelkom Estimated Marginal Means kot Term 1 izberemo našo spremenljivko Čas in izberemo Output možnost Marginal means plots. Jamovi bo izrisal povprečno vrednost vseh pacientov, dodali bomo še standardno napako za povprečje s pomočjo okvirjev. To izberemo z možnostjo Error bars: Standard error.

V oknu Results se nam izvede analiza podatkov. Zanima nas tabela Tests of sphericity, ki nam pove, ali lahko predpostavimo enako varianco pri vseh skupinah meritev. Prav tako nas zanima tabela Within Subjects Effects, ki pove ali je izbran faktor statistično značilen.

P-vrednost v tabeli Tests of sphericity, ki je manjša od 0.05 pomeni, da meritve nimajo enake variance. Zato je potrebno v tabeli Within Subjects Effects gledati test po Greenhouse-Geisser korekciji. V primeru, da je p-vrednost v tabeli Tests of sphericity večja od 0.05 zaključimo, da meritve imajo enako varianco in v tabeli Within Subjects Effects gledamo prvo vrsto, ki nima korekcije (None).

Graf v rezultatih nam prikazuje vrednosti kreatinina pri pacientih brez okvare delovanja ledvic (AKIN = 0). Pri odčitavanju tega grafa moramo biti pozorni na skalo. Opazimo, da se vrednosti kreatinina pri pacientih AKIN = 0 ne spreminjajo drastično. Ta graf je podoben pričakovanemu poteku kreatinina pri zdravih pacientih iz grafa 1. V primeru, da se vse točke s standardno napako med sabo sekajo pomeni, da ni statistično značilnih razlik, razen v primeru kreatinina po 24h in 48h. Zato lahko sklepamo, da ne bi smelo biti statistično značilnih razlik med vsemi meritvami kreatinina, razen zadnjega primera, pa še ta je mejni.

Pogledamo še rezultate testa ANOVA:

Vrednost p < 0.001 v tabeli Tests of Sphericity pomeni, da meritve nimajo enake variance in moramo v tabeli Within Subjects Effects gledati p-vrednost v vrstici z rezultati testa Greenhouse-Geisser.

Iz tabele Within Subjects Effects gledamo, ali je čas statistično pomemben faktor. Ugotovimo F = 10.215 in p < 0.001. Tako lahko trdimo, da je čas meritev kreatinina statistično pomemben faktor pri pacientih iz skupine AKIN = 0. To je nepričakovano, vendar iz grafa ugotovimo, da obstaja statistično značilna razlika med meritvami kreatinina po 24h z meritvami kreatinina po 48h, kar posledično da takšen rezultat statistične analize.

Iz post hoc analize ugotovimo, da pri pacientih brez okvare delovanja ledvic obstajajo statistično značilne razlike v meritvah kreatinina:

a. pred operacijo in 24h po operaciji,
b. med operacijo in 2h po operaciji,
c. med operacijo in 24h po operaciji,
d. 2h po operaciji in 48h po operaciji,
e. 24h po operaciji in 48h po operaciji.

Izvedimo še analizo za skupino pacientov z okvaro delovanja ledvic (AKIN = 1). S pomočjo že ustvarjenega filtra (Filters), spremenimo možnost izbire pacientov in izberemo AKIN = 1. V zavihku Data preverimo ali res uporabljamo le podatke pacientov z okvaro delovanja ledvic.

Ob tej spremembi se nam prej opisana analiza izvede samodejno, glede na podatke, ki so izbrani s pomočjo ustreznega filtra. V desnem oknu Results dobimo naslednje rezultate:

Graf kreatinina pri pacientih z okvaro delovanja ledvic (AKIN = 1) nam pokaže, da se vrednosti kreatinina razlikujejo ob različnih časih merjenja. Graf na naših podatkih je podoben pričakovanemu poteku kreatinina pri bolnih pacientih iz grafa 1. Če se na grafu intervali zaupanja v oceno povprečja med sabo ne sekajo, potem lahko trdimo, da obstajajo statistično značilne razlike med temi meritvami. Glede na dobljeni graf lahko ugotovimo statistično značilne razlike v meritvah kreatinina po 24h in 48h z meritvami kreatinina pred operacijo, med operacijo in 2h po operaciji. Iz grafa ne moremo ugotoviti, da je kreatinin 2h po operaciji statistično značilno različen od prejšnjih meritev kreatinina.

Poglejmo še rezultate testa ANOVA:

Pri podatkih za paciente z okvaro delovanja ledvic (AKIN = 1), prav tako ne moremo predpostaviti enake variance med skupinami meritev (p < 0.001). Zato v tabeli Within Subjects Effects gledamo rezultate testa Greenhouse-Geisser v drugi vrstici.

Ugotovimo, da je tudi pri skupini pacientov z okvaro delovanja ledvic čas statistično pomemben faktor za vrednosti kreatinina, saj imamo F = 31.776 in p < 0.001. Na podlagi primerjave s skupino AKIN = 0 lahko ugotovimo, da se zaradi višje F-vrednosti meritve kreatinina bolj razlikujejo po času, kot v primeru zdravih pacientov (AKIN = 0).

Iz post hoc analize ugotovimo, da pri skupini pacientov z okvaro delovanja ledvic povsod obstajajo statistično značilne razlike v meritvah kreatinina, razen pri kreatininu merjenim pred in med operacijo in kreatininu merjenim 24h in 48h po operaciji.

Končne ugotovitve

Na podlagi statistične analize meritev kreatinina ob različnih časih pri pacientih z okvaro delovanja ledvic in brez okvare, smo ugotovili tipičen potek povišanja vrednosti kreatinina pri skupini z okvaro delovanja ledvic in približno enake vrednosti kreatinina pri zdravih pacientih.

Povišanje vrednosti kreatinina pri pacientih z okvaro delovanja ledvic je statistično značilno, kar smo pokazali z analizo variance s ponovljivimi meritvami (F = 31.8, p < 0.001). Tudi v skupini brez okvare delovanja ledvic smo ugotovili statistično značilne vrednosti kreatinina (F = 10.2, p < 0.001), vendar iz grafa lahko razberemo, da je bilo to na račun vrednosti kreatinina 24h po operaciji, ki se statistično značilno razlikuje od kreatinina merjenega 48h po operaciji.

S pomočjo post hoc analize natančno določimo katere vrednosti kreatinina se med seboj statistično značilno razlikujejo.

5.7 Neparametrične verzije ANOVE

Navodila vaje

Pri vajah iz pog. 5.5 in pog. 5.6 smo izvajali enosmerno ANOVA na različnih podatkih, vendar nismo preverjali normalne porazdeljenosti vzorcev, ampak smo normalnost kar predpostavili. Pri tej vaji bomo najprej preverili normalnost podatkov pri vajah iz pog. 5.5 in pog. 5.6 ter nato glede na ugotovitve, izvedli še neparametrične verzije ANOVE.

Pri vaji iz pog. 5.5 na meritvah impedančne spektroskopije na različnih tkivih dojke po biopsiji izvedite test normalnosti vzorcev vseh skupin meritev in nato izvedite neparametrično verzijo enosmerne ANOVE s Kruskal-Wallisovim testom. Rezultate primerjajte s parametrično verzijo ANOVE.
Pri vaji iz pog. 5.6 na ponovljenih meritvah kreatinina pri pacientih z in brez delovanja funkcije ledvic izvedite test normalnosti vzorcev vseh skupin meritev in nato izvedite neparametrično verzijo enosmerne ANOVE s Friedmanovim testom. Rezultate primerjajte s parametrično verzijo ANOVE.

Postopek reševanja

V programu Jamovi odpremo podatke iz pog. 5.5, tako kot smo to naredili v prvem koraku vaje iz pog. 5.5.

Najprej preverimo normalno porazdeljenost vzorcev z ukazom Analyses -> Exploration -> Descriptives.

Zanima nas porazdelitev spremenljivke I0, glede na tip tkiva, zato za odvisno spremenljivko (Variables) izberemo I0, faktorska spremenljivka (Split by) pa je Class. Pod razdelkom Statistics pri Normality izberemo izračun Shapiro-Wilk.

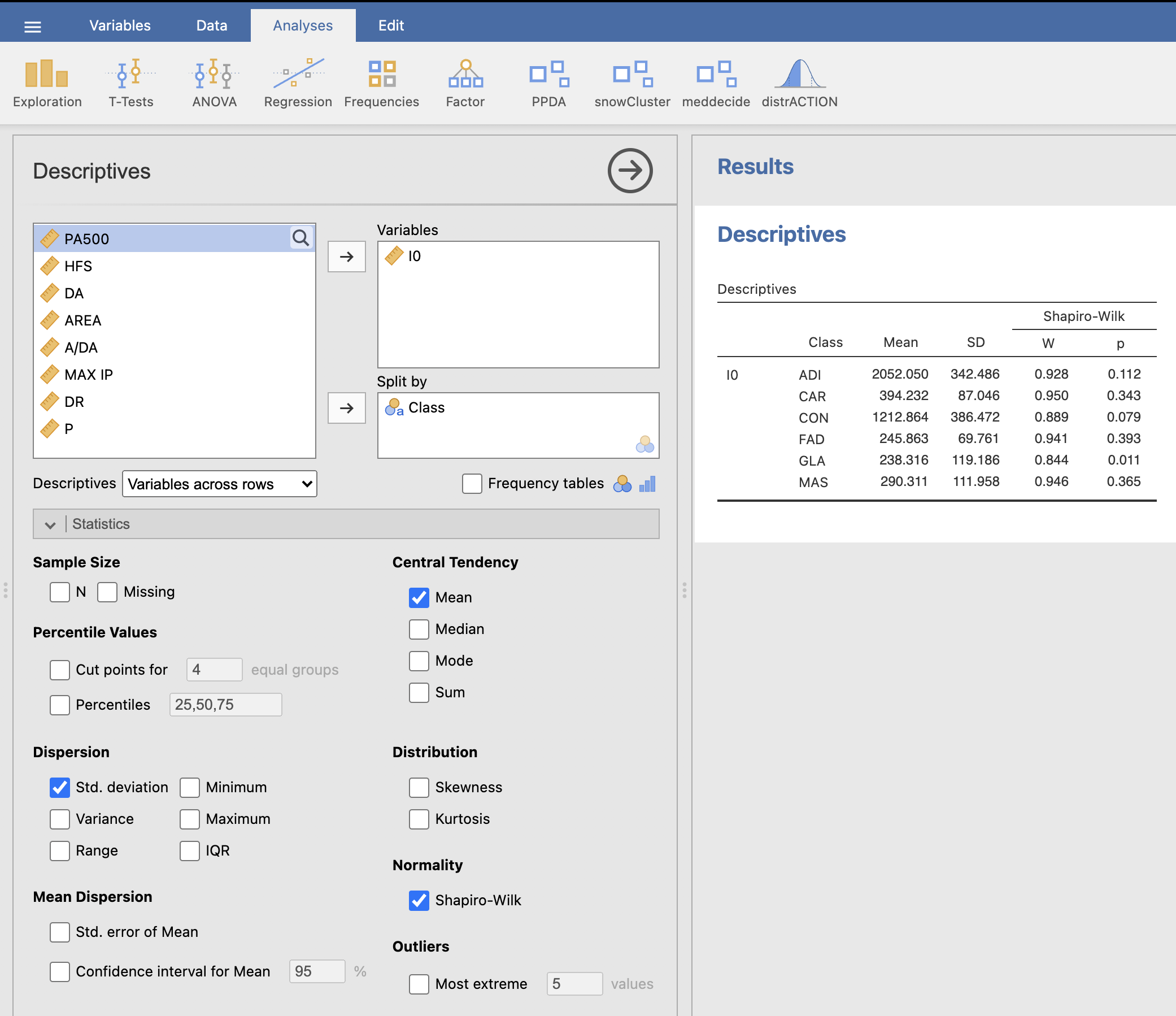
V desnem oknu Results se nam izpišejo rezultati testa normalnosti. Na podlagi Shapiro-Wilkovega testa lahko ugotovimo, da meritve spremenljivke I0 niso normalno porazdeljene pri tkivu GLA (p = 0.011).

Za ugotavljanje ustreznosti meritve I0 za ločevanje med tkivi bomo uporabili ANOVO. Ker naše meritve niso normalno porazdeljene in med seboj niso odvisne bomo uporabili neparametrični Kruskal-Wallisov test.

Izvedemo ukaz Analyses -> ANOVA in pod Non-Parametric izberemo One-Way ANOVA Kruskal-Wallis.

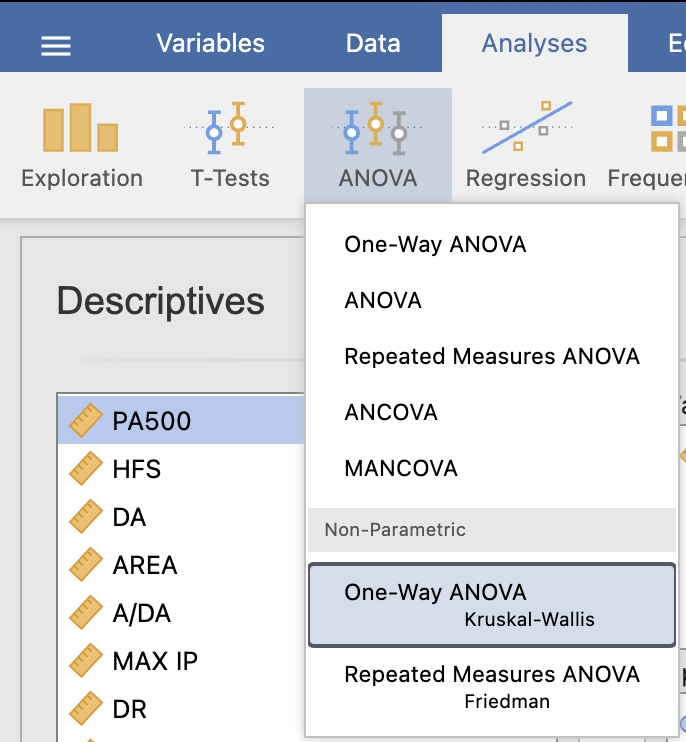
Pod Dependent Vaiables določimo spremenljivko, ki jo bomo testirali (I0) glede na tip tkiva (Grouping Variable = Class). V desnem oknu rezultatov se izpiše končni rezultat statistične analize s Kruskal-Wallisovim testom.

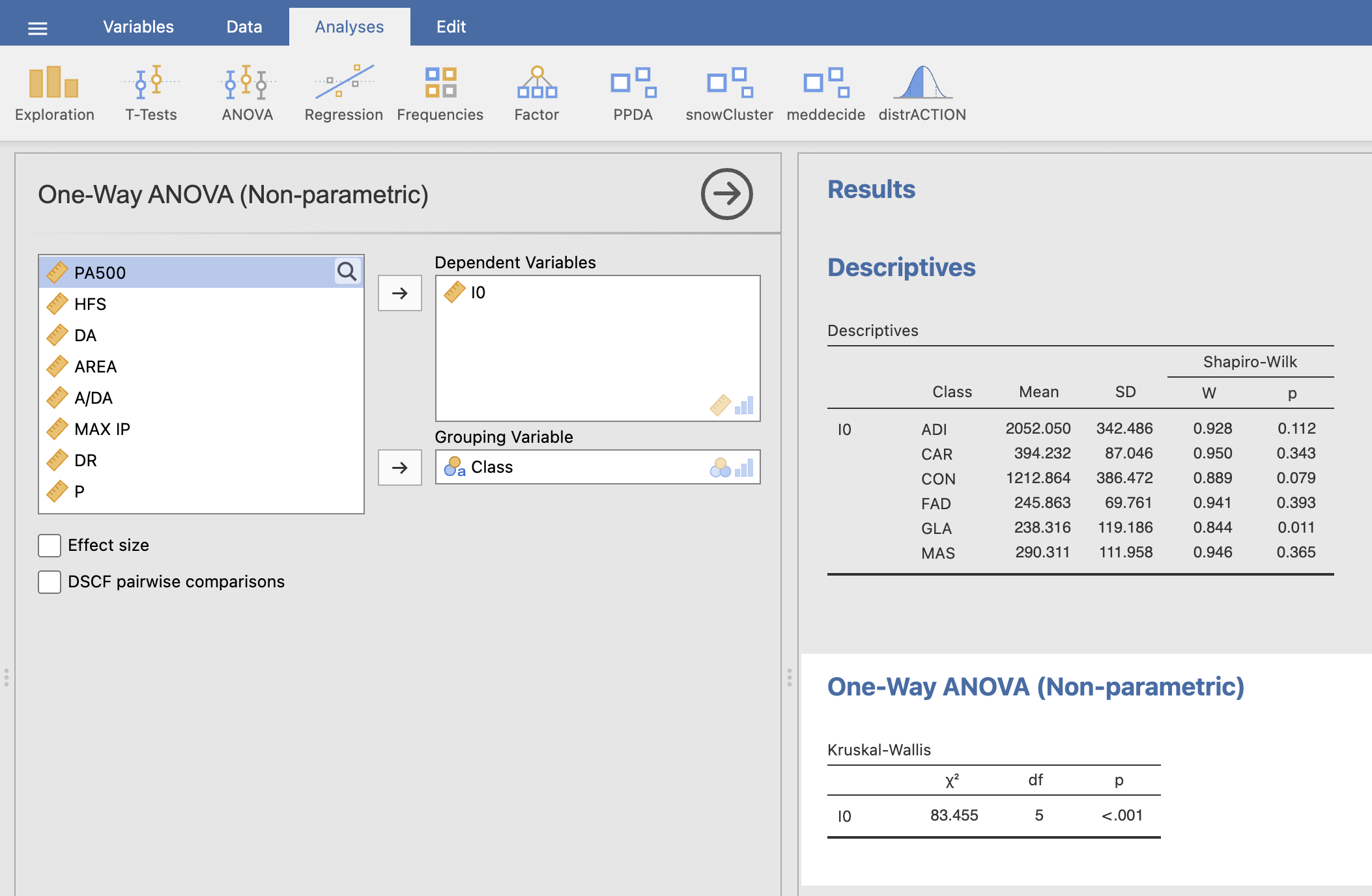
Rezultat testa pove, da je I0 statistično pomemben faktor za ločevanje med tkivi (p < 0.001).

Poglejmo še vajo iz pog. 5.6. Tu bi radi pokazali, ali se meritve kreatinina pri pacientih pri srčnih operacijah po času razlikujejo. To smo v nalogi iz pog. 5.6 izvedli z ANOVA s ponovljivimi meritvami ločeno pri pacientih z in brez motenj delovanja ledvic.

Najprej pripravimo podatke za analizo kot smo to storili v začetnih korakih pri vaji iz pog. 5.6. Izvedemo analizo najprej za skupino pacientov brez okvare delovanja ledvic (Filters: AKIN = 0).

Testiramo normalno porazdeljenost meritev z ukazom Analyses -> Exploration -> Descriptives. Izberemo spremenljivke kreatinina za analizo pod Variables, pod razdelkom Statistics pri Normality pa izberemo izračun Shapiro-Wilk.

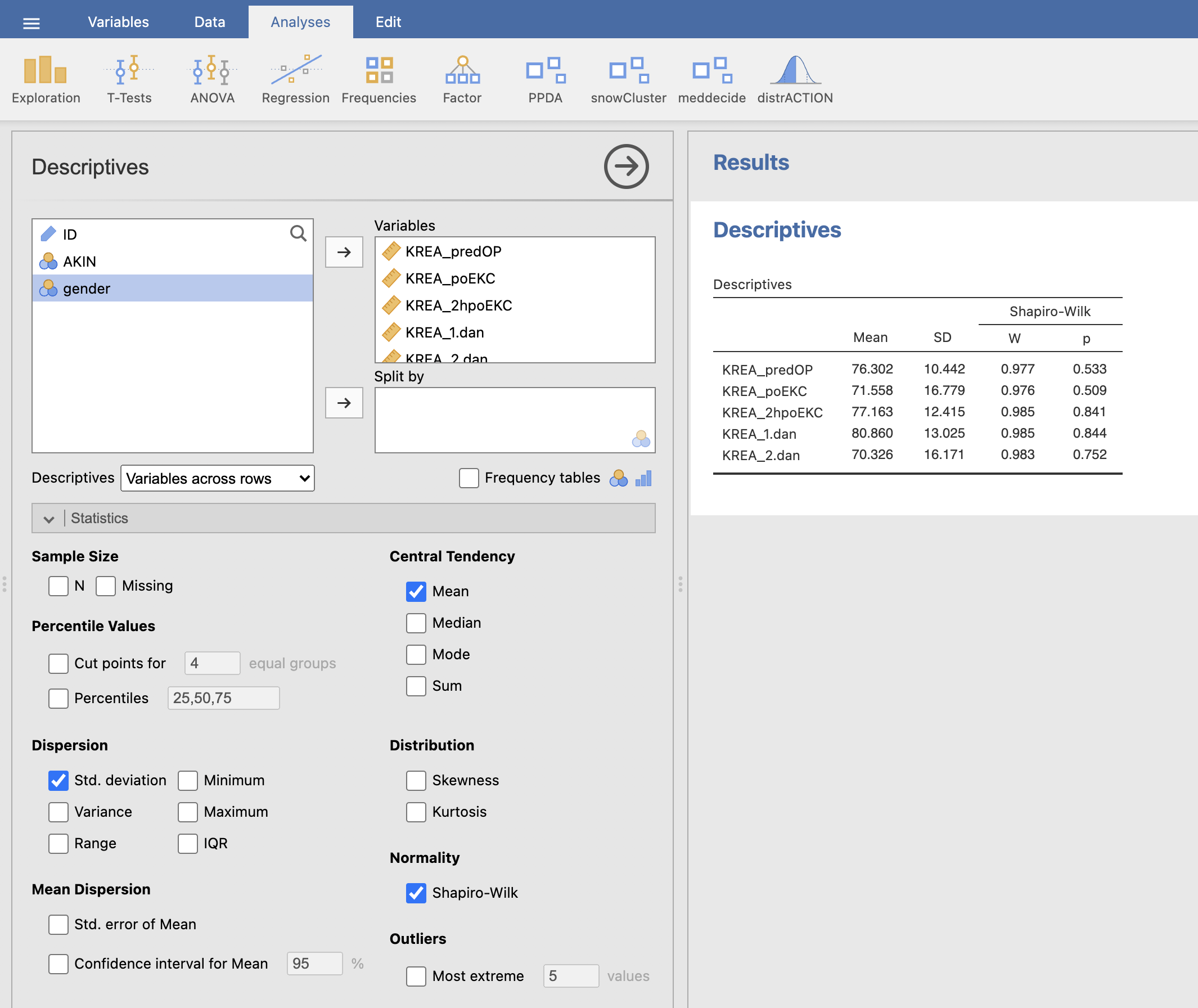
V desnem rezultatskem oknu se nam izpišejo rezultati testa normalnosti. Na podlagi Shapiro-Wilkovega testa lahko ugotovimo, da so vse meritve kreatinina pri skupini pacientov brez okvare delovanja ledvic (AKIN = 0) normalno porazdeljene.

Ponovimo teste normalnosti za skupino pacientov z okvaro delovanja ledvic (Filters: AKIN = 1).

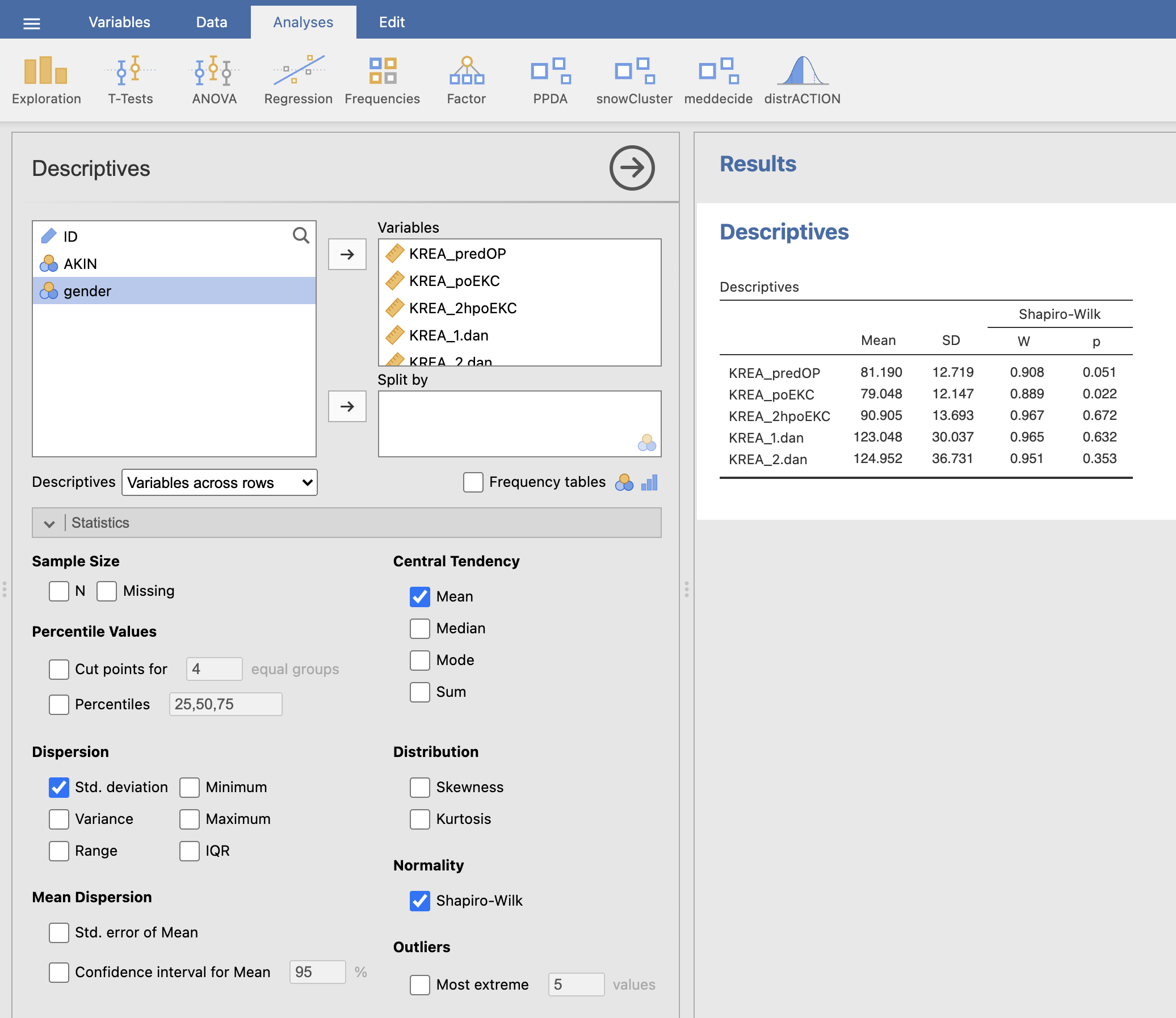
V oknu rezultati se nam izpišejo rezultati testa normalnosti. Na podlagi Shapiro-Wilkovega testa lahko ugotovimo, da meritev kreatinina med operacijo (kreatinin po EKC) pri skupini pacientov z okvaro delovanja ledvic (AKIN = 1) ni normalno porazdeljena.

Na podlagi rezultatov se odločimo, da bomo neparametrično verzijo ANOVE izvedli samo pri skupini pacientov pri AKIN = 1.

Izvedemo Friedmanov test na meritvah kreatinina pri skupini AKIN = 1 z ukazom: Analyses -> ANOVA in pod Non-Parametric izberemo Repeated Measures ANOVA Friedman.

Pod Measures izberemo spremenljivke kreatinina, ki jih bomo testirali. V desnem oknu Results se izpišejo rezultati Friedmanovega testa.

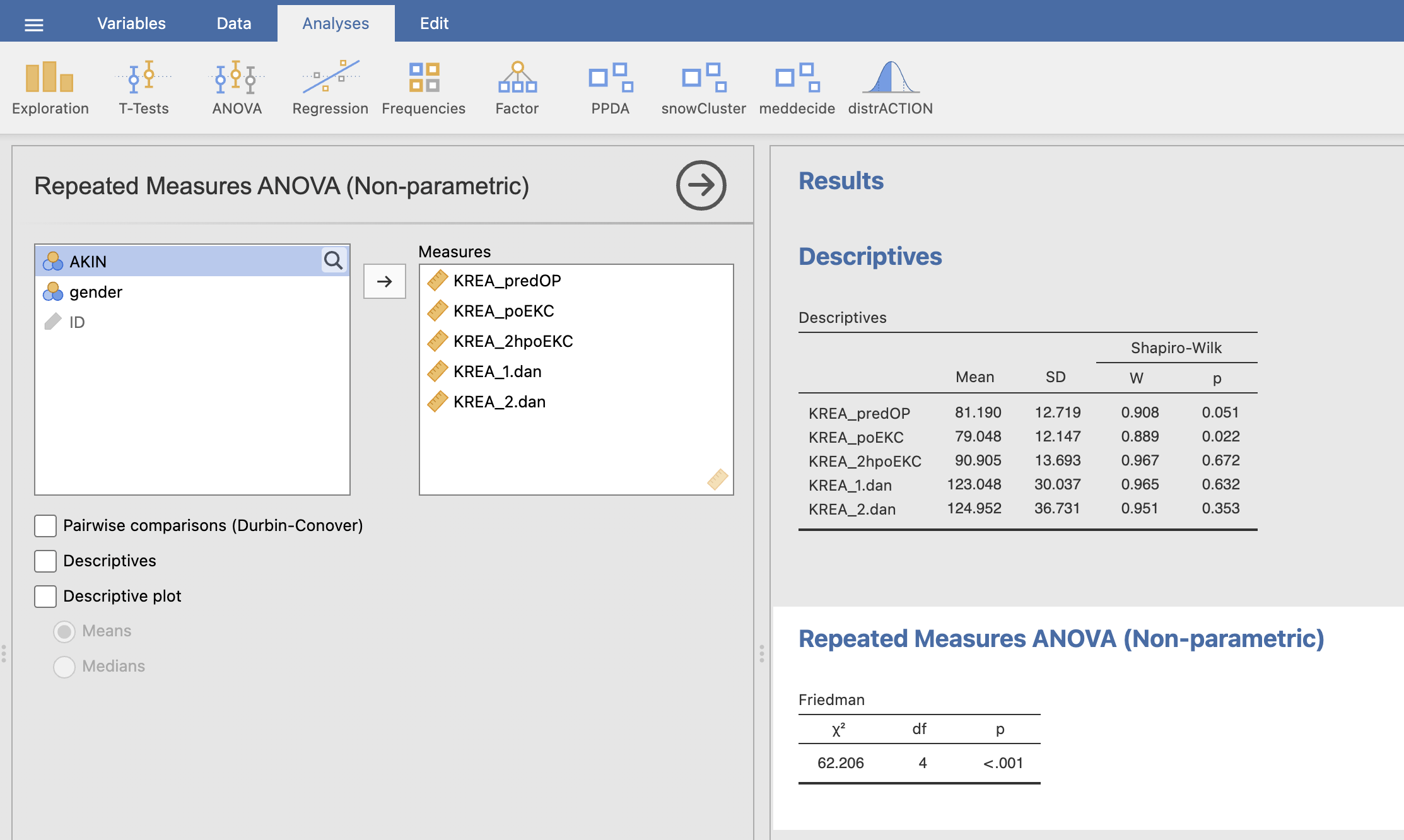
Rezultat Friedmanovega testa pove, da so časovne meritve kreatinina pri skupini AKIN = 1 statistično značilno različne (p < 0.001).

Končne ugotovitve

V primeru, ko meritve niso normalno porazdeljene, namesto ANOVE uporabljamo neparametrične verzije testov, in sicer v primeru enosmerne ANOVA z neodvisnimi meritvami uporabimo Kruskal-Wallisov test, v primeru enosmerne ANOVA z odvisnimi meritvami pa Friedmanov test.

Rezultati analize so v tem primeru enaki kot pri vajah iz pog. 5.5 in pog. 5.6, vendar smo v obeh primerih uporabili teste, ki so bolj pravilni za analizo v primeru, ko meritve niso normalno porazdeljene.

5.8 Dvosmerna ANOVA

Navodila vaje

Denimo, da merimo število povpraševanj po nekem izdelku glede na način oglaševanja izdelka v časopisih. Podatki o številu povpraševanj so zbrani v datoteki oglasevanje.xlsx. Podatki so zbrani glede na dan oglaševanja in glede na vrsto časopisa (lokalne, finančne, športne novice). Podatke smo za vsako kombinacijo zbrali 4-krat (različni časopisi).

Testiramo hipotezo, ali se povpraševanja po izdelku razlikujejo glede na dan oglaševanja in mesto oglasa v časopisu. Ker imamo dva faktorja, to naredimo z dvosmerno ANOVA.
1. Najprej podatke uredimo, da jih lahko testiramo z ANOVA v Jamovi.
2. Nato izrišemo grafe, ki bi bili primerni za prikaz števila povpraševanja glede na oba faktorja.
3. Izvedemo dvo-smerno analizo variance v Jamovi. Kaj ugotovimo? Kako si razložimo interakcijo med obema faktorjema?
4. Naredimo še post-hoc analizo z obema faktorjema, da ugotovimo, katere kombinacije oglaševanja odstopajo od drugih.

Postopek reševanja

Hočemo ugotoviti, kateri dan v tednu in v kateri tip časopisa se nam splača oglaševati izdelek, da bo povpraševanje največje.

Odpremo datoteko oglasevanje.xlsx v Excelu. Podatki so v naslednji obliki:

V podatkih imamo tri spremenljivke: dan, tip novic, število povpraševanj. Tako lahko ugotovimo, da podatki niso pravilno organizirani, zato jih v Jamovi vpišemo tako, da bo vsaka spremenljivka v svojem stolpcu. Slika prikazuje odsek pravilno vpisanih podatkov v Jamovi.

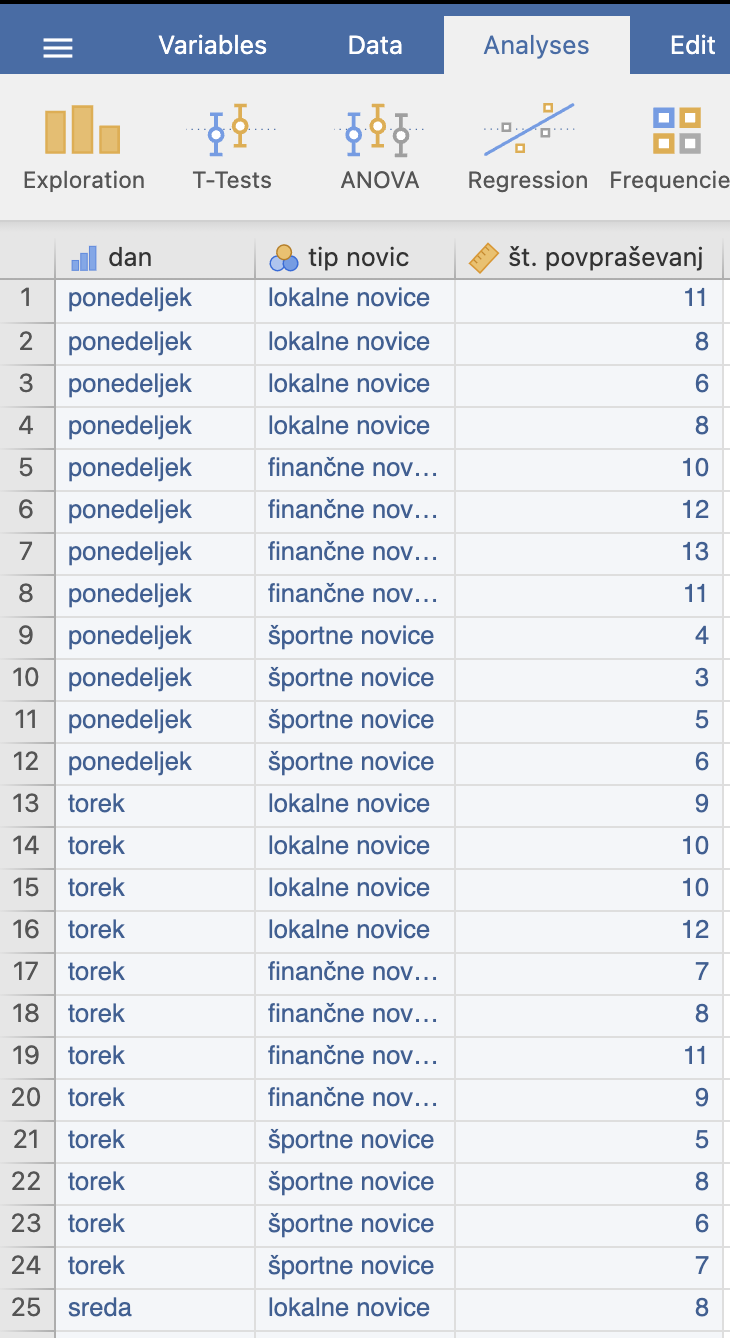
Ker želimo število povpraševanj, ki je skalarna spremenljivka, napovedovati z dvema faktorjema: dan in tip novic, ki sta kategorijski spremenljivki, bomo uporabili test ANOVA z dvema faktorjema.

Testirali bomo 3 hipoteze:

Ali je dan statistično značilen faktor za število povpraševanj?
Ali je tip novic statistično značilen faktor za število povpraševanj?
Ali je interakcija obeh faktorjev statistično pomembna za število povpraševanj?

Najprej izrišimo stolpični diagram: Analyses -> Exploration -> Descriptives; pod Variables izberemo spremenljivko št. povpraševanj, pod Split by pa spremenljivki dan in tip novic. Pod razdelkom Plots izberemo izris stolpičnega diagrama: Bar Plot. V desnem oknu se nam izriše graf.

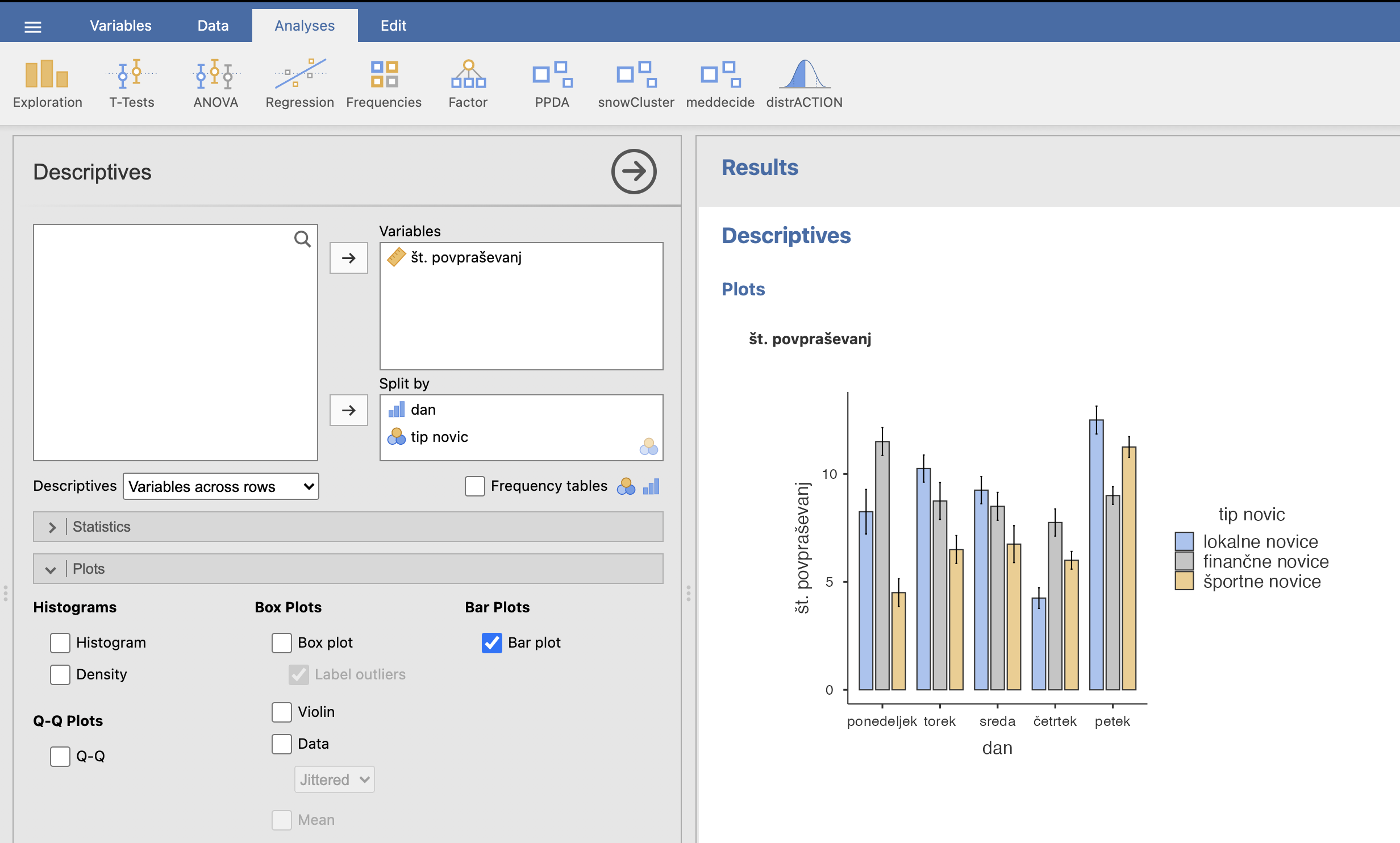Iz grafa lahko razberemo, da smo imeli v povprečju največ povpraševanj v petek pri lokalnih novicah.

Če nas zanima, ali obstaja statistično značilna razlika v povpraševanju med dnevi gledamo graf tako, da ne upoštevamo barv, primerjamo le dneve med sabo. Opazimo lahko, da je bilo v petek največ povpraševanj in v četrtek najmanj.

Če nas zanima, ali obstaja statistično značilna razlika med tipi novic gledamo graf tako, da ne upoštevamo dni, enake barve damo skupaj. Na tak način lahko opazimo, da je bilo največ povpraševanj pri lokalnih novicah (modra barva).

Če nas zanima, ali je interakcija obeh faktorjev statistično pomembna gledamo graf tako, da preverjamo, ali so porazdelitve znotraj dni glede na novice proporcionalno podobne. Če gledamo na graf tako, lahko opazimo, da so oblike torka, srede in petka podobne, drugih dveh dni (ponedeljek in četrtek) pa ne.

Izvedemo test ANOVA z dvema faktorjema: Analyses -> ANOVA -> ANOVA.

Kot odvisno spremenljivko določimo št. povpraševanj, kot faktorja pa spremenljivki dan in tip novic. Pod razdelkom Post Hoc Tests dodamo oba faktorja in označimo korekciji No correction in Tukey. Kriterij No correction bomo uporabili pri post hoc analizi tipa novic, ker so trije različni tipi. Kriterij Tukey pa bomo gledali pri post hoc analizi za spremenljivko dan, saj imamo več kot 3 primerjave med dnevi.

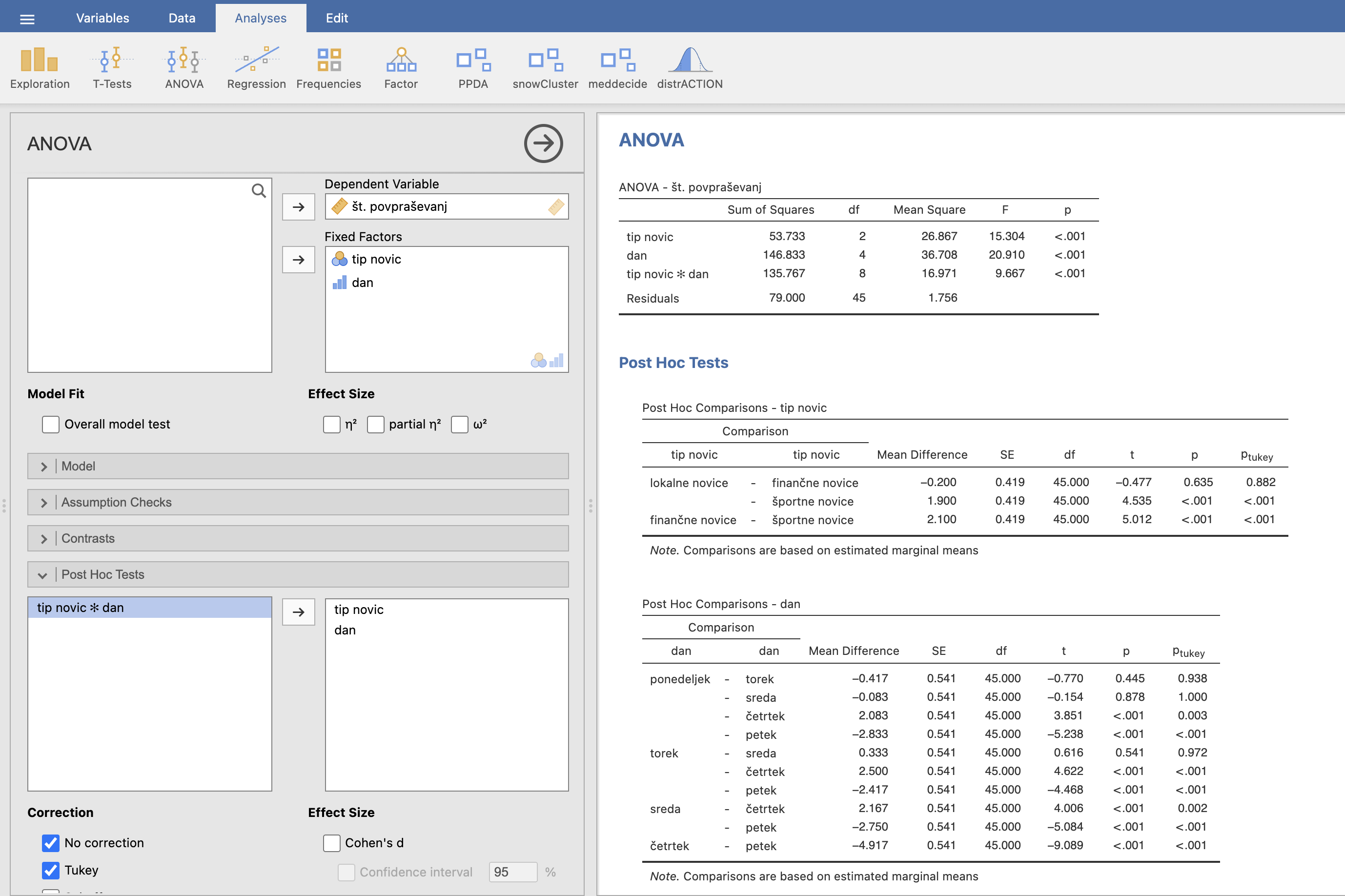
V desnem oknu Results se nam izvede statistika in izrišejo tabele. Iz analize lahko ugotovimo, da je dan statistično značilen faktor s F = 20.910 in p < 0.001. Tip novic je statistično značilen faktor s F = 15.304 in p < 0.001. Interakcija je statistično značilna s F = 9.667 in p < 0.001. Pri primerjavi vrednosti F-statistike opazimo, da je za povpraševanje najpomembnejši faktor dan, potem tip novic in nazadnje interakcija med faktorjema.

Pri Post hoc analizi faktorja dan gledamo vrednosti kriterija Tukey:

Lahko ugotovimo, da se četrtek statistično značilno razlikuje od vseh ostalih dni in ima najmanjše povpraševanje, saj so razlike med četrtkom in ostalimi dnevi negativne. Tako lahko zaključimo, da je četrtek najslabši dan za povpraševanje.
Petek je statistično značilno različen od vseh ostalih dni s pozitivnimi razlikami, kar pomeni, da so tu v povprečju največja povpraševanja. Zato lahko zaključimo, da je petek najboljši dan za oglaševanje.
Pri primerjavi ostalih dni opazimo, da niso statistično značilno različni med seboj, zato je vseeno, v katerem izmed teh dni bomo izvedli oglaševanje.

Pri Post hoc analizi faktorja tip novic gledamo vrednosti pri kriteriju No correction:

Finančne novice se statistično značilno razlikujejo od športnih novic (p < 0.001), ne pa od lokalnih novic (p = 0.635). Razlika je pozitivna, kar pomeni da je povpraševanje v finančnih novicah večje kot v športnih novicah.
Lokalne novice se statistično značilno razlikujejo od športnih novic (p < 0.001). Povpraševanje je zaradi pozitivne razlike večje v lokalnih kot v športnih novicah.

Končne ugotovitve

Ko želimo napovedovati neko skalarno spremenljivko z dvema faktorjema, ki sta kategorijski spremenljivki, moramo uporabiti test ANOVA z dvema faktorjema. Ugotoviti moramo ali vsak posamezen faktor vpliva na skalarno spremenljivko in ali vpliva tudi interakcija med faktorjema.

S post hoc analizo ugotavljamo, katere kombinacije faktorja se razlikujejo od drugih in na kakšen način. V primeru, ko je vrednost razlike povprečij pozitivna, pomeni da je faktor pri prvi vrednosti večji kot pri drugi. V primeru, ko je vrednost razlike povprečij negativna pa pomeni, da je faktor pri prvi vrednosti manjši kot pri drugi.

V našem primeru oglaševanja z dvosmerno analizo variance lahko ugotovimo naslednje:

dan v tednu je statistično značilen faktor za oglaševanje (F = 20.910, p < 0.001).
tip novic je statistično značilen faktor za oglaševanje (F = 15.304 in p < 0.001),
interakcija obeh faktorjev je tudi statistično značilna (F = 9.667 in p < 0.001).
najpomembnejši faktor za število povpraševanj dan, potem tip novic in nato interakcija glede na izračunane F-vrednosti pri ANOVI.

S post-hoc analizo (kriterij Tukey) ugotovimo, da oglaševanje v petek statistično značilno odstopa od ostalih dni po povpraševanju (vse p < 0.001). Povpraševanje je večje od ostalih dni. Četrtek tudi statistično značilno odstopa od ostalih dni z nižjim povpraševanjem. Povpraševanje pri ostalih dnevih se statistično značilno ne razlikuje.

S post hoc analizo tipa novic (kriterij No correction) lahko ugotovimo, da je povpraševanje statistično značilno najnižje v športnih novicah (p < 0.001), pri finančnih in lokalnih novicah pa ni statistično značilne razlike (p = 0.635).

Iz analize ugotovimo, da je za največje povpraševanje potrebno oglaševati v petek v finančnih ali v lokalnih novicah. Najslabše povpraševanje pa je v športnih novicah in ob četrtkih.